人教版高一物理必修一:3.5 力的分解——正交分解法(共20张PPT)
文档属性
| 名称 | 人教版高一物理必修一:3.5 力的分解——正交分解法(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 534.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
正交分解法
学会正交分解法求合力
解决复杂平衡问题
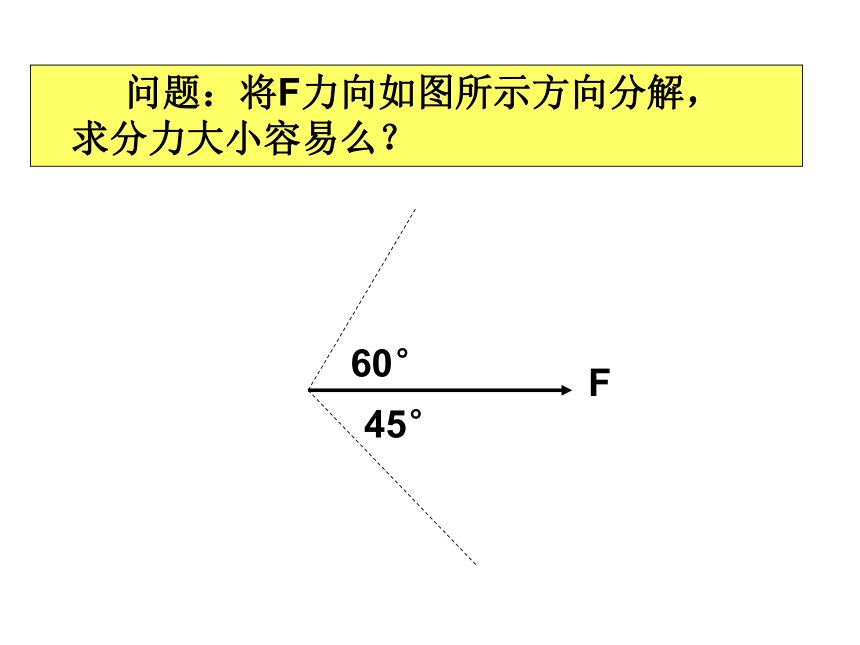
45°
60°
F
问题:将F力向如图所示方向分解,
求分力大小容易么?
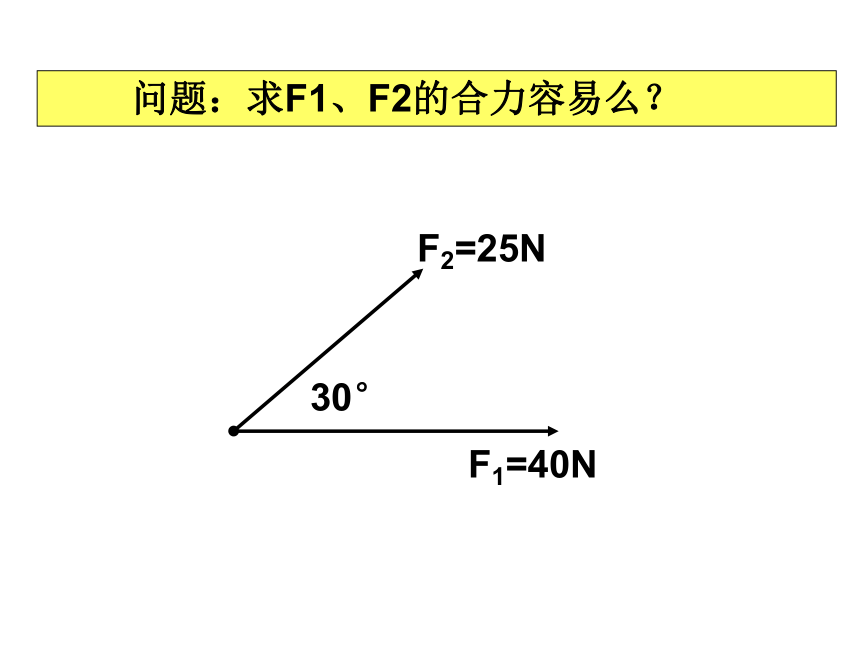
F1=40N
F2=25N
30°
问题:求F1、F2的合力容易么?
F=100N
╮
θ =30°
已知F=100N,两分力的方向互相垂直,如图
求出:两个分力的大小
F1
F2
F2=Fsin θ=100×0.5=50N
问题:将F力向如图所示方向分解,
求分力大小容易么?
F1=40N
F2=25N
30°
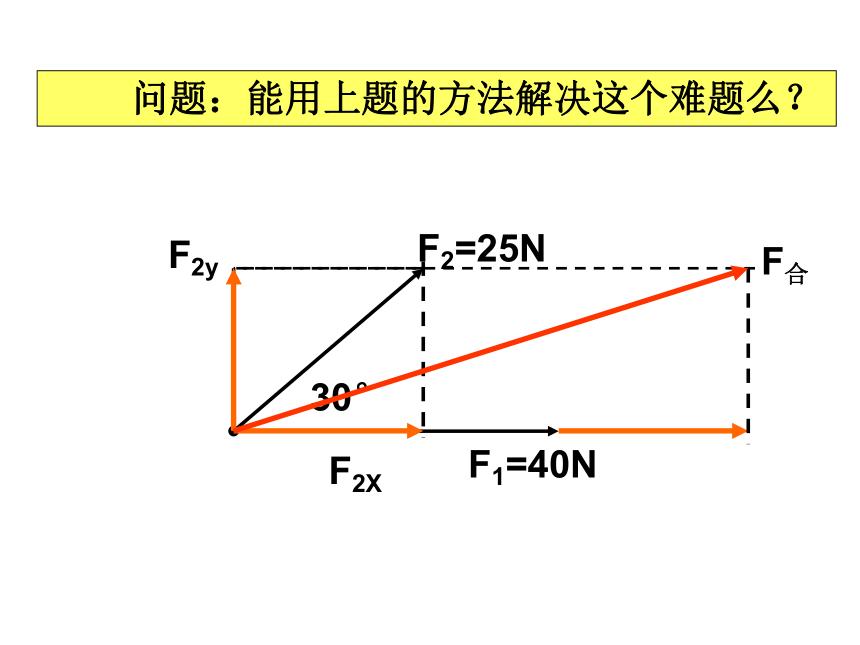
问题:能用上题的方法解决这个难题么?
F2X
F2y
F合
力的正交分解
1)把物体受到的各个力都分解到互相垂直的两个方向x轴、y轴上去
2)先求这两个方向上的力Fx和Fy,再用Fx、Fy求最终的合力。
在求多个力的合力时,可以把复杂问题简化
用正交分解的方法,先将力分解再合成
力的正交分解
(1)定义:把一个已知力沿着两个互相
垂直的方向进行分解
(2)正交分解步骤:
①建立xoy直角坐标系
②沿xoy轴将各力分解
③求x、y轴上的合力Fx,Fy
F1
F2
F3
x
y
O
F2y
F1y
F3y
F3x
F1x
F2X
y轴为正向:Fy=F1y+F2y-F3y
x轴为正向:Fx=F1x+F3x-F2x
若物体匀速运动,合力为零,则:Fx=0;Fy=0
F1
F2
F3
x
y
O
F2y
F1y
F3y
F3x
F1x
F2X
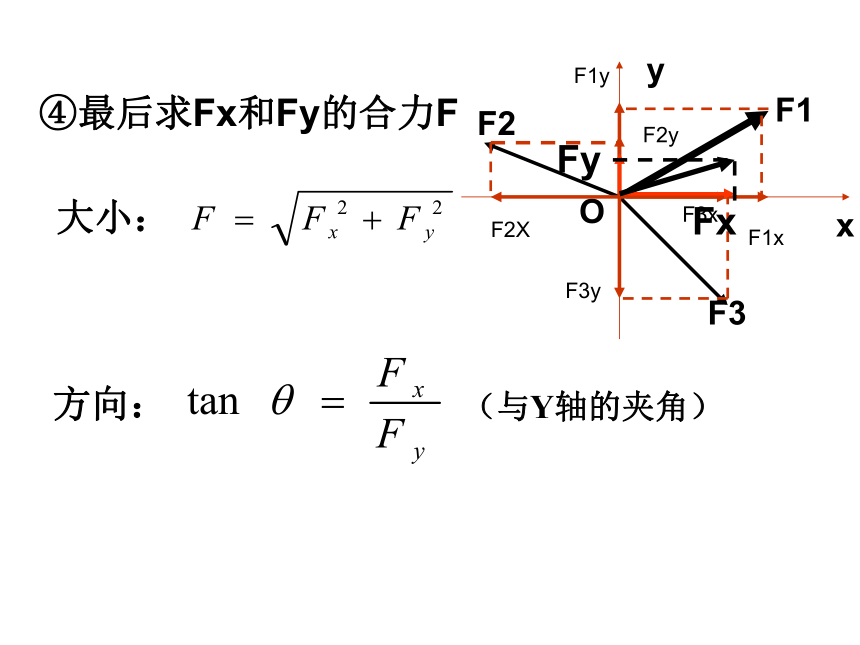
④最后求Fx和Fy的合力F
大小:
方向:
(与Y轴的夹角)
Fy
Fx
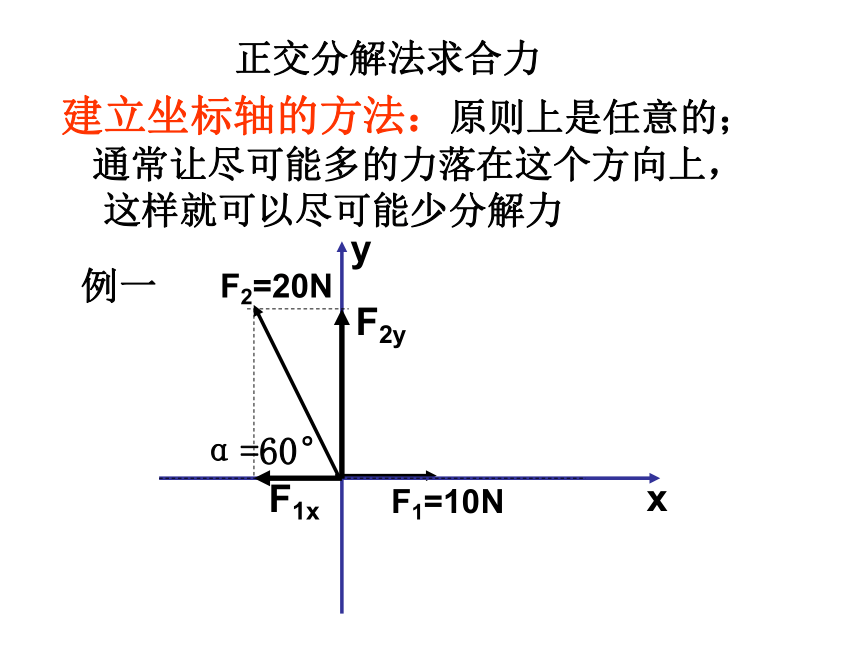
正交分解法求合力
建立坐标轴的方法:原则上是任意的;
通常让尽可能多的力落在这个方向上,
这样就可以尽可能少分解力
F1=10N
F2=20N
x
y
α=60°
F2y
F1x
例一
F1=100N
F2=60N
F3=80N
α=37°
求三个力的合力
┕
例二
┕
α
已知: F1=3.6N 、F2=6N 、F3=3N ,F2与虚线
方向夹角α=37°,求三个力的合力
F1
F2
F3
例三
正交分解法解决平衡问题
物体静止和匀速运动都是平衡态
平衡态物体所受力的合力为零
正交分解时,两个轴上的分力的合力必为零。
即 ∑Fx=0
∑Fy=0.
这样就建立了两个方程,组成方程组,求解问题
通常沿着速度方向建立坐标轴
质量为m的物体沿粗糙斜面匀速下滑,
斜面倾角为α,
求:物体受到的支持力和摩擦力
物体与斜面的动摩擦因数多大?
┕
G
N
f
α
物体匀速运动,合力为零
X轴方向:f=mgsin α---1)
Y轴方向:N=mgcos α –2)
例四
据:f=μN---3)
1)2)3)联立,可得:
μ=tan α
α
例五: 木箱重500 N,放在水平地面上,一个人用大小为200 N与水平方向成30°向上的力拉木箱,木箱沿地平面匀速运动,求木箱受到的摩擦力和地面所受的压力。
解:画出物体受力图,如图所示。
由于物体在水平方向和竖直方向都处于平衡状态,所以
补充问题:物体与地面间的动摩擦因数多大?
所求:
例六: 木箱重500 N,放在水平地面上,一个人用大小为200 N与水平方向成30°向下的力推木箱,木箱沿地平面匀速运动,求木箱与地面的动摩擦因数。
30°
θ
例题7:质量为m的物体放在倾角为θ的斜面上,在平行斜面的推力的作用下,物体沿斜面匀速
运动。物体与斜面的动摩擦因数为μ
1)若向上运动,求:推力的大小______
斜面对物体支持力的大小______
F
2)若向下运动,求:推力的大小________
斜面对物体支持力的大小________
G
θ
例题8:质量为m的物体放在倾角为θ的光滑斜面上,在水平恒定推力的作用下,物体沿斜面匀速
向下运动。
求:水平推力的大小_____________
斜面对物体支持力的大小__________
N
F
G
θ
例题8:质量为m的物体放在倾角为θ的粗糙斜面上,动摩擦因数为μ,在水平恒定推力的作用下,物体沿斜面匀速向下运动。
求:水平推力的大小_____________
斜面对物体支持力的大小__________
N
F
例题9:质量为m的物体压在竖直墙面上,外力与水平方向夹角为θ。物体与斜面的滑动摩擦因数为μ,在推力的作用下,物体沿墙面匀速向上运动,则物体受到的推力的大小是( )
若物体沿墙面匀速向下运动,
则物体受到的推力的大小是( )
F
θ
正交分解法
学会正交分解法求合力
解决复杂平衡问题
45°
60°
F
问题:将F力向如图所示方向分解,
求分力大小容易么?
F1=40N
F2=25N
30°
问题:求F1、F2的合力容易么?
F=100N
╮
θ =30°
已知F=100N,两分力的方向互相垂直,如图
求出:两个分力的大小
F1
F2
F2=Fsin θ=100×0.5=50N
问题:将F力向如图所示方向分解,
求分力大小容易么?
F1=40N
F2=25N
30°
问题:能用上题的方法解决这个难题么?
F2X
F2y
F合
力的正交分解
1)把物体受到的各个力都分解到互相垂直的两个方向x轴、y轴上去
2)先求这两个方向上的力Fx和Fy,再用Fx、Fy求最终的合力。
在求多个力的合力时,可以把复杂问题简化
用正交分解的方法,先将力分解再合成
力的正交分解
(1)定义:把一个已知力沿着两个互相
垂直的方向进行分解
(2)正交分解步骤:
①建立xoy直角坐标系
②沿xoy轴将各力分解
③求x、y轴上的合力Fx,Fy
F1
F2
F3
x
y
O
F2y
F1y
F3y
F3x
F1x
F2X
y轴为正向:Fy=F1y+F2y-F3y
x轴为正向:Fx=F1x+F3x-F2x
若物体匀速运动,合力为零,则:Fx=0;Fy=0
F1
F2
F3
x
y
O
F2y
F1y
F3y
F3x
F1x
F2X
④最后求Fx和Fy的合力F
大小:
方向:
(与Y轴的夹角)
Fy
Fx
正交分解法求合力
建立坐标轴的方法:原则上是任意的;
通常让尽可能多的力落在这个方向上,
这样就可以尽可能少分解力
F1=10N
F2=20N
x
y
α=60°
F2y
F1x
例一
F1=100N
F2=60N
F3=80N
α=37°
求三个力的合力
┕
例二
┕
α
已知: F1=3.6N 、F2=6N 、F3=3N ,F2与虚线
方向夹角α=37°,求三个力的合力
F1
F2
F3
例三
正交分解法解决平衡问题
物体静止和匀速运动都是平衡态
平衡态物体所受力的合力为零
正交分解时,两个轴上的分力的合力必为零。
即 ∑Fx=0
∑Fy=0.
这样就建立了两个方程,组成方程组,求解问题
通常沿着速度方向建立坐标轴
质量为m的物体沿粗糙斜面匀速下滑,
斜面倾角为α,
求:物体受到的支持力和摩擦力
物体与斜面的动摩擦因数多大?
┕
G
N
f
α
物体匀速运动,合力为零
X轴方向:f=mgsin α---1)
Y轴方向:N=mgcos α –2)
例四
据:f=μN---3)
1)2)3)联立,可得:
μ=tan α
α
例五: 木箱重500 N,放在水平地面上,一个人用大小为200 N与水平方向成30°向上的力拉木箱,木箱沿地平面匀速运动,求木箱受到的摩擦力和地面所受的压力。
解:画出物体受力图,如图所示。
由于物体在水平方向和竖直方向都处于平衡状态,所以
补充问题:物体与地面间的动摩擦因数多大?
所求:
例六: 木箱重500 N,放在水平地面上,一个人用大小为200 N与水平方向成30°向下的力推木箱,木箱沿地平面匀速运动,求木箱与地面的动摩擦因数。
30°
θ
例题7:质量为m的物体放在倾角为θ的斜面上,在平行斜面的推力的作用下,物体沿斜面匀速
运动。物体与斜面的动摩擦因数为μ
1)若向上运动,求:推力的大小______
斜面对物体支持力的大小______
F
2)若向下运动,求:推力的大小________
斜面对物体支持力的大小________
G
θ
例题8:质量为m的物体放在倾角为θ的光滑斜面上,在水平恒定推力的作用下,物体沿斜面匀速
向下运动。
求:水平推力的大小_____________
斜面对物体支持力的大小__________
N
F
G
θ
例题8:质量为m的物体放在倾角为θ的粗糙斜面上,动摩擦因数为μ,在水平恒定推力的作用下,物体沿斜面匀速向下运动。
求:水平推力的大小_____________
斜面对物体支持力的大小__________
N
F
例题9:质量为m的物体压在竖直墙面上,外力与水平方向夹角为θ。物体与斜面的滑动摩擦因数为μ,在推力的作用下,物体沿墙面匀速向上运动,则物体受到的推力的大小是( )
若物体沿墙面匀速向下运动,
则物体受到的推力的大小是( )
F
θ
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
