北师大版七年级数学下册1.1 同底数幂的乘法课件(共27张)
文档属性
| 名称 | 北师大版七年级数学下册1.1 同底数幂的乘法课件(共27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-26 00:00:00 | ||
图片预览






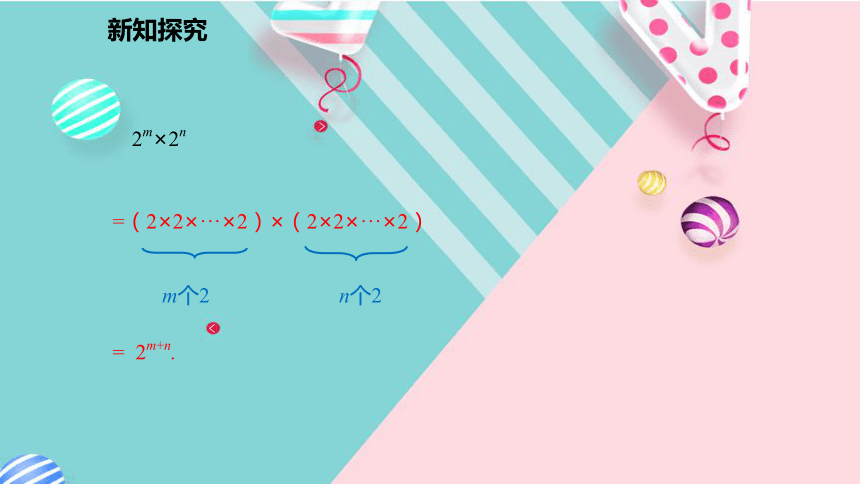
文档简介
课件27张PPT。第一章
整式的乘除1.1 同底数幂的乘法七年级数学北师版·下册教学目标1、经历探索同底数幂乘法运算性质的过程,进一步体会幂的意义,发展推理能力和有条理的表达能力.
2、了解同底数幂乘法的运算性质,并能解决一些实际问题.新课导入光在真空中的速度大约是 3×108m/s.太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要4.22年.一年以3×107秒计算,比邻星与地球的距离约为多少?3×108×3×107×4.22= 37.98× (108×107).
108×107等于多少呢?
108×107=1015.新课导入1.计算下列各式:
(1)102×103 ;
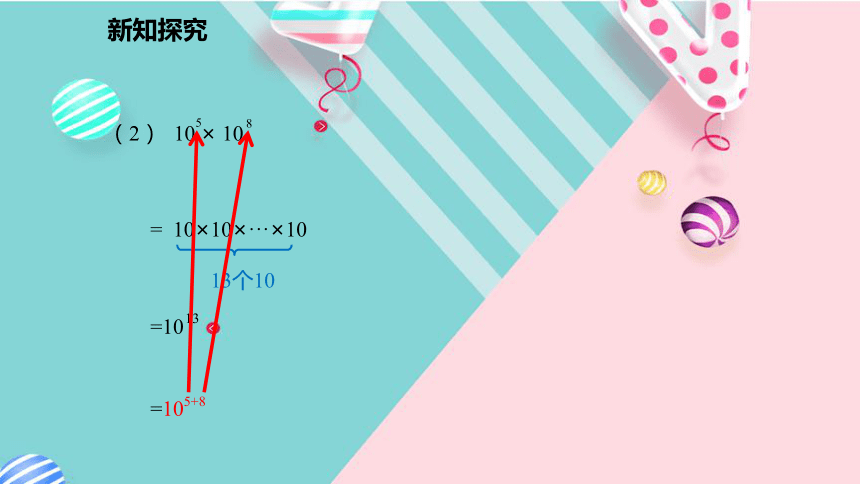
(2)105×108 ;
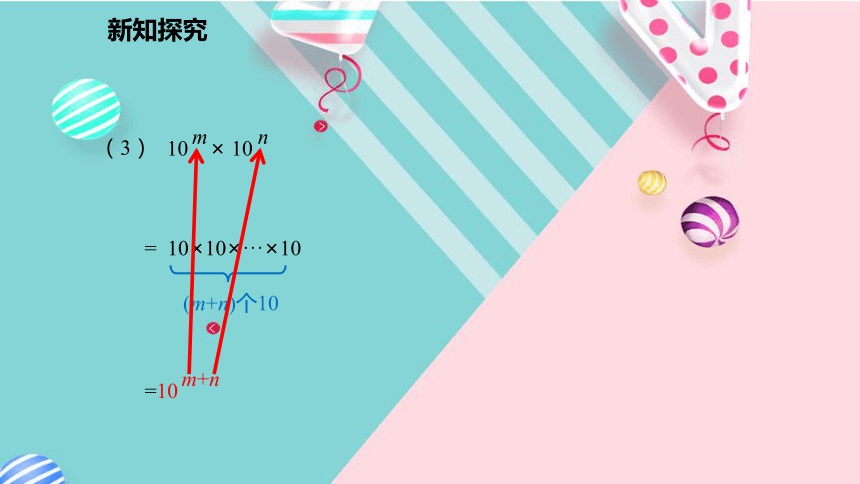
(3)10m×10n(m,n 都是正整数).= 10×10×10×10×10=105(1)=102+3新知探究新知探究=105+8新知探究新知探究2.2m×2n等于什么?
( )m× ( )n 呢?
(m,n都是正整数)新知探究= 2m+n. m个2 n个22m×2n=(2×2×···×2)×(2×2×···×2) 新知探究 == m+nm个n个这个结论是否具有一般性?如果底数同样也是字母呢?新知探究猜想 : am · an = (当m,n都是正整数). am · an =m个an个a= a ·a· ··· ·a= am+n.(m+n)个a即:(a· a· ··· · a)·(a· a· ··· ·a)am+n(乘方的意义)(乘法结合律)(乘方的意义)证明:am · an = am+n (当m,n都是正整数).新知探究同底数幂的乘法公式:思考:当三个或三个以上同底数幂相乘时,同底数幂的乘法公式是否也适用呢?怎样用公式表示? am·an·ap= am+n+p (m,n,p都是正整数).am · an = am+n (当m,n都是正整数).新知探究例1.计算:
(1)(-3)7×(-3)6;
(2)( )3×( ) ;
(3)-x3·x5 ;
(4)b2m ·b2m+1 .新知探究解:(1)(-3)7×(-3)6 =(-3)7+6 =(-3)13.
(2)( )3×( ) =( )3 +1 =( ) 4.
(3)-x3·x5 = -x3+5 = -x8.
(4)b2m ·b2m+1 =b2m+ 2m+1=b4m+1 .同底数幂(底数相同的幂)的乘法法则:
同底数幂相乘,底数不变,指数相加 .用字母表示:
am· an =am+n (m,n是正整数).新知探究例2.光在真空中的速度约为 3×10 8 m/s,太阳光照射到地球上大约需要5×102 s.地球距离太阳大约有多远?分析:
1.因为速度乘以时间等于距离,所以用光的速度乘以所有的时间即得地球和太阳的距离.
2.所得结果要用科学记数法来表示.注意科学记数法表示数的形式新知探究解: 3×108× 5×102
= 15×1010
= 1.5×1011(m).
答:地球距离太阳大约有 1.5×1011m.新知探究1、a · a9 = a2 · a8 = a3 · ( )
=( ) · ( )=( ) · ( )
2、am+n = ( )· an
3、am+n+2 = ( )· an · ( )逆用同底数幂的乘法性质时,可把一个幂分成两个或多个同底数幂的乘积,底数与原底数相同,指数的和等于原来幂的指数.a7a4a6a5a5amama2同底数幂的乘法性质的逆运用:新知探究1.计算:
(1)52×57 ; (2)7×73×72 ;
(3)- x2 · x3 ; (4)( -c) 3 · (-c) m .新知探究1.解:
(1)5 2 × 5 7 = 5 2+7 = 5 9 .
(2)7 × 7 3 × 7 2 = 7 1+3+2 = 7 6 .
(3)- x 2 · x 3 = - x2+3 = - x5 .
(4)( - c ) 3 · ( - c ) m = ( - c ) 3 +m.2.一种电子计算机每秒可做 4×109 次运算,它工作 5×102 s 可做多少次运算?解: (4×109 )×(5×102)=20×1011 =2×1012.
答:工作 5×102 s 可做2×1012次运算. 新知探究新知探究同底数幂乘法公式的应用及注意事项
三点应用:
1.可把一个幂写成几个相同底数幂的乘积.
2.可逆用同底数幂的乘法公式进行计算或说理.
3.可把一些实际问题转化为同底数幂的乘法进行求解.
两点注意:
1.转化过程中要时刻注意幂的底数相同.
2.解题中要注意整体思想的应用.新知探究填空:
(1) 16 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .456课堂小结1.同底数幂的乘法表达式:2.法则:同底数幂相乘,底数不变,指数相加.am · an = am+n (当m,n都是正整数). am · an · ap = am+n+p (m,n,p都是正整数).课堂小测1. (2a)3 · (2a)m等于( )
A.3(2a)m-4 B.(2a)m-1
C.(2a)m+3 D.(2a)m+1 解析: (2a)3 · (2a)m=(2a)m+3.
C课堂小测2. an · am 等于( )
A.am-n B.amn
C.am+a+n D.am+n 解析: an · am= am+n .
D课堂小测3. xa+n 可以写成( )
A.xa · xn B.xa +xn
C.x+xn D.axn 解析: xa · xn = xa+n .A课堂小测4. -a · (-a)4 · (-a)b = a8,则b=_______. 分析:根据同底数幂的乘法法则可完成此题.3解答:-a · (-a)4 · (-a)b = (-a)1+4+b = a8,故b=3.
2、了解同底数幂乘法的运算性质,并能解决一些实际问题.新课导入光在真空中的速度大约是 3×108m/s.太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要4.22年.一年以3×107秒计算,比邻星与地球的距离约为多少?3×108×3×107×4.22= 37.98× (108×107).
108×107等于多少呢?
108×107=1015.新课导入1.计算下列各式:
(1)102×103 ;
(2)105×108 ;
(3)10m×10n(m,n 都是正整数).= 10×10×10×10×10=105(1)=102+3新知探究新知探究=105+8新知探究新知探究2.2m×2n等于什么?
( )m× ( )n 呢?
(m,n都是正整数)新知探究= 2m+n. m个2 n个22m×2n=(2×2×···×2)×(2×2×···×2) 新知探究 == m+nm个n个这个结论是否具有一般性?如果底数同样也是字母呢?新知探究猜想 : am · an = (当m,n都是正整数). am · an =m个an个a= a ·a· ··· ·a= am+n.(m+n)个a即:(a· a· ··· · a)·(a· a· ··· ·a)am+n(乘方的意义)(乘法结合律)(乘方的意义)证明:am · an = am+n (当m,n都是正整数).新知探究同底数幂的乘法公式:思考:当三个或三个以上同底数幂相乘时,同底数幂的乘法公式是否也适用呢?怎样用公式表示? am·an·ap= am+n+p (m,n,p都是正整数).am · an = am+n (当m,n都是正整数).新知探究例1.计算:
(1)(-3)7×(-3)6;
(2)( )3×( ) ;
(3)-x3·x5 ;
(4)b2m ·b2m+1 .新知探究解:(1)(-3)7×(-3)6 =(-3)7+6 =(-3)13.
(2)( )3×( ) =( )3 +1 =( ) 4.
(3)-x3·x5 = -x3+5 = -x8.
(4)b2m ·b2m+1 =b2m+ 2m+1=b4m+1 .同底数幂(底数相同的幂)的乘法法则:
同底数幂相乘,底数不变,指数相加 .用字母表示:
am· an =am+n (m,n是正整数).新知探究例2.光在真空中的速度约为 3×10 8 m/s,太阳光照射到地球上大约需要5×102 s.地球距离太阳大约有多远?分析:
1.因为速度乘以时间等于距离,所以用光的速度乘以所有的时间即得地球和太阳的距离.
2.所得结果要用科学记数法来表示.注意科学记数法表示数的形式新知探究解: 3×108× 5×102
= 15×1010
= 1.5×1011(m).
答:地球距离太阳大约有 1.5×1011m.新知探究1、a · a9 = a2 · a8 = a3 · ( )
=( ) · ( )=( ) · ( )
2、am+n = ( )· an
3、am+n+2 = ( )· an · ( )逆用同底数幂的乘法性质时,可把一个幂分成两个或多个同底数幂的乘积,底数与原底数相同,指数的和等于原来幂的指数.a7a4a6a5a5amama2同底数幂的乘法性质的逆运用:新知探究1.计算:
(1)52×57 ; (2)7×73×72 ;
(3)- x2 · x3 ; (4)( -c) 3 · (-c) m .新知探究1.解:
(1)5 2 × 5 7 = 5 2+7 = 5 9 .
(2)7 × 7 3 × 7 2 = 7 1+3+2 = 7 6 .
(3)- x 2 · x 3 = - x2+3 = - x5 .
(4)( - c ) 3 · ( - c ) m = ( - c ) 3 +m.2.一种电子计算机每秒可做 4×109 次运算,它工作 5×102 s 可做多少次运算?解: (4×109 )×(5×102)=20×1011 =2×1012.
答:工作 5×102 s 可做2×1012次运算. 新知探究新知探究同底数幂乘法公式的应用及注意事项
三点应用:
1.可把一个幂写成几个相同底数幂的乘积.
2.可逆用同底数幂的乘法公式进行计算或说理.
3.可把一些实际问题转化为同底数幂的乘法进行求解.
两点注意:
1.转化过程中要时刻注意幂的底数相同.
2.解题中要注意整体思想的应用.新知探究填空:
(1) 16 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .456课堂小结1.同底数幂的乘法表达式:2.法则:同底数幂相乘,底数不变,指数相加.am · an = am+n (当m,n都是正整数). am · an · ap = am+n+p (m,n,p都是正整数).课堂小测1. (2a)3 · (2a)m等于( )
A.3(2a)m-4 B.(2a)m-1
C.(2a)m+3 D.(2a)m+1 解析: (2a)3 · (2a)m=(2a)m+3.
C课堂小测2. an · am 等于( )
A.am-n B.amn
C.am+a+n D.am+n 解析: an · am= am+n .
D课堂小测3. xa+n 可以写成( )
A.xa · xn B.xa +xn
C.x+xn D.axn 解析: xa · xn = xa+n .A课堂小测4. -a · (-a)4 · (-a)b = a8,则b=_______. 分析:根据同底数幂的乘法法则可完成此题.3解答:-a · (-a)4 · (-a)b = (-a)1+4+b = a8,故b=3.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
