陕西省黄陵中学高新部2019-2020学年高二上学期期末考试数学(文)试题(word解析版)
文档属性
| 名称 | 陕西省黄陵中学高新部2019-2020学年高二上学期期末考试数学(文)试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 78.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-27 18:40:38 | ||
图片预览




文档简介
2019—2020学年度第一学期高新高二期末数学(文)试题
一、选择题(共12小题,每小题5.0分,共60分)
1.下列对算法的理解不正确的是( )
A.一个算法应包含有限的步骤,而不能是无限的
B.算法中的每一步骤都应当是确定的,而不应当是含糊的、模棱两可的
C.算法中的每一步骤应当有效地执行,并得到确定的结果
D.一个问题只能设计出一种算法
2.表达算法的基本逻辑结构不包括( )
A.顺序结构 B.条件结构 C.循环结构 D.计算结构
3.如图所示的程序框图的运行结果是( )
A. B. C. D.3
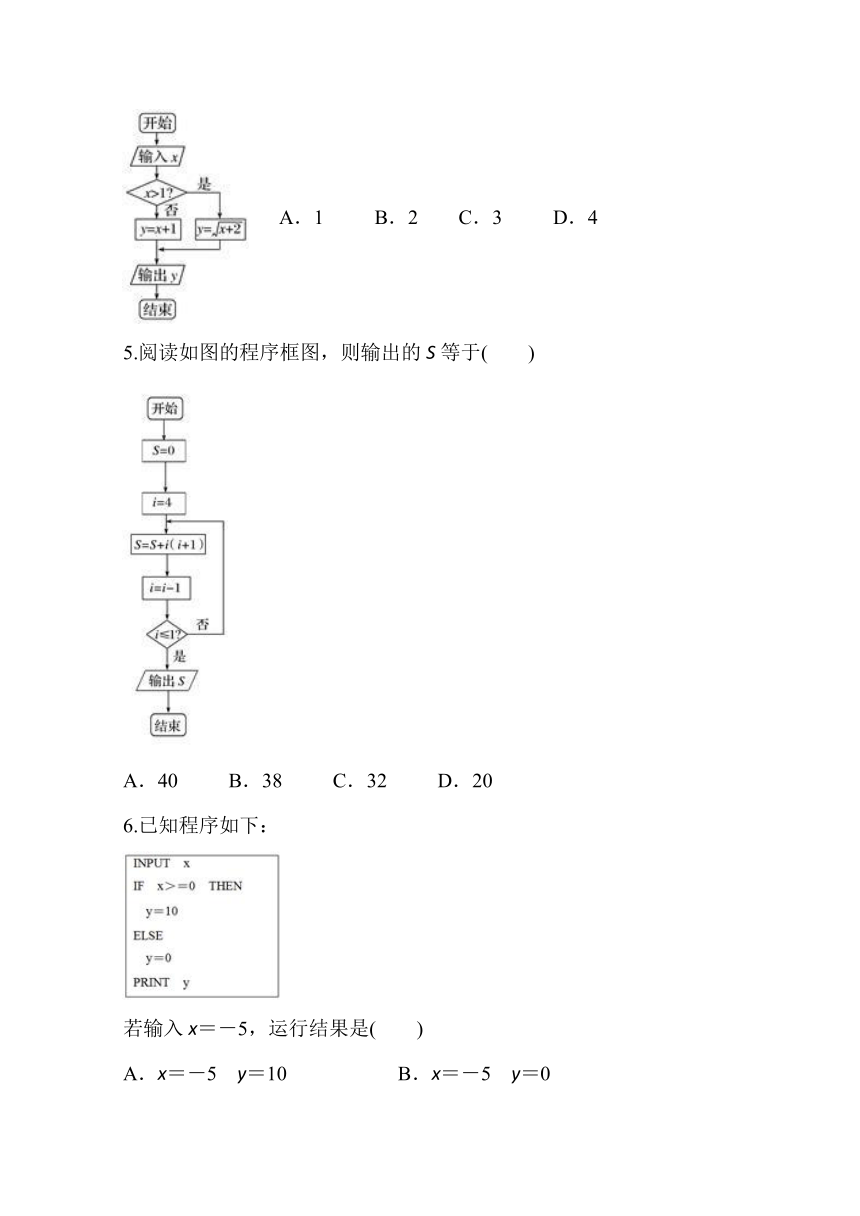
4.如图所示的程序框图中,输入x=2,则输出的结果是( )
A.1 B.2 C.3 D.4
5.阅读如图的程序框图,则输出的S等于( )
A.40 B.38 C.32 D.20
6.已知程序如下:
若输入x=-5,运行结果是( )
A.x=-5 y=10 B.x=-5 y=0
C.y=100 D.y=0
7.下面程序运行后,输出的值是( )
A.8 B.9 C.10 D.11
8.把十进制数20化为二进制数为( )
A.10 000(2) B.10 100(2) C.11 001(2) D.10 001(2)
9.下列问题中,最适合用简单随机抽样方法抽样的是( )
A.某报告厅有32排座位,每排有40个座位,座位号是1~40,有一次报告厅坐满了观众,报告会结束以后听取观众的意见,要留下32名观众进行座谈
B.从十台冰箱中抽取3台进行质量检验
C.某学校有在编人员160人,其中行政人员16人,教师112人,后勤人员32人.教育部门为了解大家对学校机构改革的意见,要从中抽取容量为20的样本
D.某乡农田有山地8 000亩,丘陵12 000亩,平地24 000亩,洼地4 000亩,现抽取农田480亩估计全乡农田平均产量
10.已知x,y的取值如下表所示:
如果y与x线性相关,且线性回归方程为=x+,则等于( )
A. B. C. D.1
11.从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B=“抽到二等品”,事件C=“抽到三等品”,已知P(A)=0.65,P(B)=0.2,P(C)=0.1,则事件“抽到的不是一等品”的概率为( )
A.0.65 B.0.35 C.0.3 D.0.005
12.甲从正方形四个顶点中任意选择两个顶点连成直线,乙也从该正方形四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是( )
A. B. C. D.
二、填空题(共4小题,每小题5.0分,共20分)
13.在一个个体数目为2 003的总体中,利用系统抽样抽取一个容量为100的样本,则总体中每个个体被抽到的机会为________.
14.200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在(50,60)的汽车大约有________辆.
15.下列事件:
①物体在重力作用下会自由下落;
②方程x2-2x+3=0有两个不相等的实数根;
③下周日会下雨;
④某寻呼台每天某一时段内收到传呼的次数少于10次.
其中随机事件的个数为________.
16.分别在区间[1,6]和[1,4]内任取一个实数,依次记为m和n,则m>n的概率为________.
三、解答题(共6小题,17-21每小题14分,第22小题10分,共80分)
17.(本题14分)
求焦点在y轴上,且经过两个点(0,2)和(1,0)的椭圆的标准方程;
18.(本题14分)
已知函数f(x)=2x3+3x2-12x+5.求曲线y=f(x)在点(0,5)处的切线方程;
19.(本题14分)
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况如下:
甲:15,17,14,23,22,24,32;
乙:12,13,11,23,27,31,30.
(1)求甲、乙两名运动员得分的中位数.
(2)分别求甲、乙两名运动员得分的平均数、方差,你认为哪位运动员的成绩更稳定?
20.(本题14分)
某企业共有3 200名职工,其中中、青、老年职工的比例为5∶3∶2,从所有职工中抽取一个容量为400的样本,应采用哪种抽样方法更合理?中、青、老年职工应分别抽取多少人?
21.(本题14分)
甲、乙两人下棋,和棋的概率为,乙胜的概率为,求:
(1)甲胜的概率; (2)甲不输的概率.
22.(本题10分)
甲、乙两人约定上午7:00至8:00之间到某站乘公共汽车,在这段时间内有3班公共汽车,它们开车时刻分别为7:20,7:40,8:00,若他们约定,见车就乘,求甲、乙同乘一车的概率.
高新高二文数学答案解析
1.【答案】D
【解析】算法的有限性是指包含步骤是有限的,故A正确;算法的确定性是指每一步都是确定的,故B正确;算法的每一步都是确定的,且每一步都应有确定的结果,故C正确;对于同一个问题可以有不同的算法,故 D错误.
2.【答案】D
【解析】基本逻辑结构只有三种.
3.【答案】C
【解析】根据程序框图的意义可知在当a=2,b=4时,S=+=,故输出.
4.【答案】B
【解析】输入x=2后,该程序框图的执行过程是:
输入x=2,
x=2>1成立,
y==2,
输出y=2.
5.【答案】B
【解析】第一次循环,S=0+4×5=20,i=3;第二次循环,S=20+3×4=32,i=2;第三次循环,S=32+2×3=38,i=1,结束循环,输出S=38.
6.【答案】D
【解析】输入-5,执行ELSE后面的语句,即y=0.
7.【答案】C
【解析】102=100,结束循环,i=10.
8.【答案】B
【解析】利用除2取余数可得.
9.【答案】B
【解析】简单随机抽样的特点.
10.【答案】B
【解析】因为=3,=5,又回归直线过点(,),所以5=3+,
所以=-.
11.【答案】B
【解析】∵抽到的不是一等品的对立事件是抽到一等品,而P(A)=0.65.∴抽到的不是一等品的概率是1-0.65=0.35.
12.【答案】C
【解析】甲从正方形四个顶点中任意选择两个顶点连成直线,乙也从正方形四个顶点中任意选择两个顶点连成直线,所得的直线共有6×6=36(对),而相互垂直的有10对,故根据古典概型概率公式得P==.
13.【答案】
【解析】在抽样过程中尽管要剔除三个个体,但每个个体被抽到的机会仍是相同的,即每个个体被抽到的概率为.
14.【答案】60
【解析】根据频率分布直方图,得
时速在(50,60)的频率为
0.03×10=0.3,
∴在该时速段的汽车大约有
200×0.3=60(辆).
15.【答案】2
【解析】结合必然事件、不可能事件、随机事件的定义作出判断;由定义可知,①是必然事件,②是不可能事件,③④是随机事件.
16.【答案】
【解析】建立平面直角坐标系(如图所示),则由图可知满足m>n的点应在梯形ABCD内,所以所求事件的概率为P==.
17.【答案】
∵椭圆的焦点在y轴上,
∴设它的标准方程为+=1(a>b>0).
又椭圆经过点(0,2)和(1,0),
∴
∴
∴所求椭圆的标准方程为+x2=1.
【解析】
18.【答案】依题意可知:f′(x)=6x2+6x-12,
k=f′(x)|x=0=-12,
∴切线方程为y-5=-12x,即12x+y-5=0.
【解析】
19.【答案】解 (1)将甲运动员得分的数据由大到小排列:32,24,23,22,17,15,14.甲运动员得分的中位数是22.同样的可知乙运动员得分的中位数是23.
(2)甲=(15+17+14+23+22+24+32)=21.
乙=(12+13+11+23+27+31+30)=21,
=[(21-15)2+(21-17)2+…+(21-32)2]=,
=[(21-12)2+(21-13)2+…(21-30)2]=,
∴<
∴甲运动员的成绩更稳定.
【解析】
20.【答案】由于中、青、老年职工有明显的差异,采用分层抽样更合理.
按照比例抽取中、青、老年职工的人数分别为:×400=200,×400=120,×400=80,
因此应抽取的中、青、老年职工分别为200人,120人,80人.
【解析】
21.【答案】(1)“甲胜”是“和棋或乙胜”的对立事件,所以甲胜的概率为1--=.
(2)方法一 设“甲不输”为事件A,可看作是“甲胜”与“和棋”这两个互斥事件的和事件,所以P(A)=+=.
方法二 设“甲不输”为事件A,可看作是“乙胜”的对立事件.所以P(A)=1-=.即甲不输的概率是.
【解析】
22.【答案】设甲到达汽车站的时间为x,乙到达汽车站的时间为y,则7≤x≤8,7≤y≤8,即甲、乙两人到达汽车站的时刻(x,y)所对应的区域在平面直角坐标系中画出(如图所示)是大正方形.将三班车到站的时刻在图形中画出,则甲、乙两人要想乘同一班车,必须满足7≤x≤7,7≤y≤7;7≤x≤7,7≤y≤7;7≤x≤8,7≤y≤8.即(x,y)必须落在图形中的三个带阴影的小正方形内,所以由几何概型的计算公式得,P==.
【解析】
一、选择题(共12小题,每小题5.0分,共60分)
1.下列对算法的理解不正确的是( )
A.一个算法应包含有限的步骤,而不能是无限的
B.算法中的每一步骤都应当是确定的,而不应当是含糊的、模棱两可的
C.算法中的每一步骤应当有效地执行,并得到确定的结果
D.一个问题只能设计出一种算法
2.表达算法的基本逻辑结构不包括( )
A.顺序结构 B.条件结构 C.循环结构 D.计算结构
3.如图所示的程序框图的运行结果是( )
A. B. C. D.3
4.如图所示的程序框图中,输入x=2,则输出的结果是( )
A.1 B.2 C.3 D.4
5.阅读如图的程序框图,则输出的S等于( )
A.40 B.38 C.32 D.20
6.已知程序如下:
若输入x=-5,运行结果是( )
A.x=-5 y=10 B.x=-5 y=0
C.y=100 D.y=0
7.下面程序运行后,输出的值是( )
A.8 B.9 C.10 D.11
8.把十进制数20化为二进制数为( )
A.10 000(2) B.10 100(2) C.11 001(2) D.10 001(2)
9.下列问题中,最适合用简单随机抽样方法抽样的是( )
A.某报告厅有32排座位,每排有40个座位,座位号是1~40,有一次报告厅坐满了观众,报告会结束以后听取观众的意见,要留下32名观众进行座谈
B.从十台冰箱中抽取3台进行质量检验
C.某学校有在编人员160人,其中行政人员16人,教师112人,后勤人员32人.教育部门为了解大家对学校机构改革的意见,要从中抽取容量为20的样本
D.某乡农田有山地8 000亩,丘陵12 000亩,平地24 000亩,洼地4 000亩,现抽取农田480亩估计全乡农田平均产量
10.已知x,y的取值如下表所示:
如果y与x线性相关,且线性回归方程为=x+,则等于( )
A. B. C. D.1
11.从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B=“抽到二等品”,事件C=“抽到三等品”,已知P(A)=0.65,P(B)=0.2,P(C)=0.1,则事件“抽到的不是一等品”的概率为( )
A.0.65 B.0.35 C.0.3 D.0.005
12.甲从正方形四个顶点中任意选择两个顶点连成直线,乙也从该正方形四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是( )
A. B. C. D.
二、填空题(共4小题,每小题5.0分,共20分)
13.在一个个体数目为2 003的总体中,利用系统抽样抽取一个容量为100的样本,则总体中每个个体被抽到的机会为________.
14.200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在(50,60)的汽车大约有________辆.
15.下列事件:
①物体在重力作用下会自由下落;
②方程x2-2x+3=0有两个不相等的实数根;
③下周日会下雨;
④某寻呼台每天某一时段内收到传呼的次数少于10次.
其中随机事件的个数为________.
16.分别在区间[1,6]和[1,4]内任取一个实数,依次记为m和n,则m>n的概率为________.
三、解答题(共6小题,17-21每小题14分,第22小题10分,共80分)
17.(本题14分)
求焦点在y轴上,且经过两个点(0,2)和(1,0)的椭圆的标准方程;
18.(本题14分)
已知函数f(x)=2x3+3x2-12x+5.求曲线y=f(x)在点(0,5)处的切线方程;
19.(本题14分)
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况如下:
甲:15,17,14,23,22,24,32;
乙:12,13,11,23,27,31,30.
(1)求甲、乙两名运动员得分的中位数.
(2)分别求甲、乙两名运动员得分的平均数、方差,你认为哪位运动员的成绩更稳定?
20.(本题14分)
某企业共有3 200名职工,其中中、青、老年职工的比例为5∶3∶2,从所有职工中抽取一个容量为400的样本,应采用哪种抽样方法更合理?中、青、老年职工应分别抽取多少人?
21.(本题14分)
甲、乙两人下棋,和棋的概率为,乙胜的概率为,求:
(1)甲胜的概率; (2)甲不输的概率.
22.(本题10分)
甲、乙两人约定上午7:00至8:00之间到某站乘公共汽车,在这段时间内有3班公共汽车,它们开车时刻分别为7:20,7:40,8:00,若他们约定,见车就乘,求甲、乙同乘一车的概率.
高新高二文数学答案解析
1.【答案】D
【解析】算法的有限性是指包含步骤是有限的,故A正确;算法的确定性是指每一步都是确定的,故B正确;算法的每一步都是确定的,且每一步都应有确定的结果,故C正确;对于同一个问题可以有不同的算法,故 D错误.
2.【答案】D
【解析】基本逻辑结构只有三种.
3.【答案】C
【解析】根据程序框图的意义可知在当a=2,b=4时,S=+=,故输出.
4.【答案】B
【解析】输入x=2后,该程序框图的执行过程是:
输入x=2,
x=2>1成立,
y==2,
输出y=2.
5.【答案】B
【解析】第一次循环,S=0+4×5=20,i=3;第二次循环,S=20+3×4=32,i=2;第三次循环,S=32+2×3=38,i=1,结束循环,输出S=38.
6.【答案】D
【解析】输入-5,执行ELSE后面的语句,即y=0.
7.【答案】C
【解析】102=100,结束循环,i=10.
8.【答案】B
【解析】利用除2取余数可得.
9.【答案】B
【解析】简单随机抽样的特点.
10.【答案】B
【解析】因为=3,=5,又回归直线过点(,),所以5=3+,
所以=-.
11.【答案】B
【解析】∵抽到的不是一等品的对立事件是抽到一等品,而P(A)=0.65.∴抽到的不是一等品的概率是1-0.65=0.35.
12.【答案】C
【解析】甲从正方形四个顶点中任意选择两个顶点连成直线,乙也从正方形四个顶点中任意选择两个顶点连成直线,所得的直线共有6×6=36(对),而相互垂直的有10对,故根据古典概型概率公式得P==.
13.【答案】
【解析】在抽样过程中尽管要剔除三个个体,但每个个体被抽到的机会仍是相同的,即每个个体被抽到的概率为.
14.【答案】60
【解析】根据频率分布直方图,得
时速在(50,60)的频率为
0.03×10=0.3,
∴在该时速段的汽车大约有
200×0.3=60(辆).
15.【答案】2
【解析】结合必然事件、不可能事件、随机事件的定义作出判断;由定义可知,①是必然事件,②是不可能事件,③④是随机事件.
16.【答案】
【解析】建立平面直角坐标系(如图所示),则由图可知满足m>n的点应在梯形ABCD内,所以所求事件的概率为P==.
17.【答案】
∵椭圆的焦点在y轴上,
∴设它的标准方程为+=1(a>b>0).
又椭圆经过点(0,2)和(1,0),
∴
∴
∴所求椭圆的标准方程为+x2=1.
【解析】
18.【答案】依题意可知:f′(x)=6x2+6x-12,
k=f′(x)|x=0=-12,
∴切线方程为y-5=-12x,即12x+y-5=0.
【解析】
19.【答案】解 (1)将甲运动员得分的数据由大到小排列:32,24,23,22,17,15,14.甲运动员得分的中位数是22.同样的可知乙运动员得分的中位数是23.
(2)甲=(15+17+14+23+22+24+32)=21.
乙=(12+13+11+23+27+31+30)=21,
=[(21-15)2+(21-17)2+…+(21-32)2]=,
=[(21-12)2+(21-13)2+…(21-30)2]=,
∴<
∴甲运动员的成绩更稳定.
【解析】
20.【答案】由于中、青、老年职工有明显的差异,采用分层抽样更合理.
按照比例抽取中、青、老年职工的人数分别为:×400=200,×400=120,×400=80,
因此应抽取的中、青、老年职工分别为200人,120人,80人.
【解析】
21.【答案】(1)“甲胜”是“和棋或乙胜”的对立事件,所以甲胜的概率为1--=.
(2)方法一 设“甲不输”为事件A,可看作是“甲胜”与“和棋”这两个互斥事件的和事件,所以P(A)=+=.
方法二 设“甲不输”为事件A,可看作是“乙胜”的对立事件.所以P(A)=1-=.即甲不输的概率是.
【解析】
22.【答案】设甲到达汽车站的时间为x,乙到达汽车站的时间为y,则7≤x≤8,7≤y≤8,即甲、乙两人到达汽车站的时刻(x,y)所对应的区域在平面直角坐标系中画出(如图所示)是大正方形.将三班车到站的时刻在图形中画出,则甲、乙两人要想乘同一班车,必须满足7≤x≤7,7≤y≤7;7≤x≤7,7≤y≤7;7≤x≤8,7≤y≤8.即(x,y)必须落在图形中的三个带阴影的小正方形内,所以由几何概型的计算公式得,P==.
【解析】
同课章节目录
