北师大版七年级数学下册4.4 用尺规作三角形课件(19张)
文档属性
| 名称 | 北师大版七年级数学下册4.4 用尺规作三角形课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-27 12:00:03 | ||
图片预览




文档简介
课件19张PPT。第四章
三角形4.4 用尺规作三角形七年级数学北师版·下册教学目标1、在给出的三角形的一些要素后能利用尺规准确地作出三角形
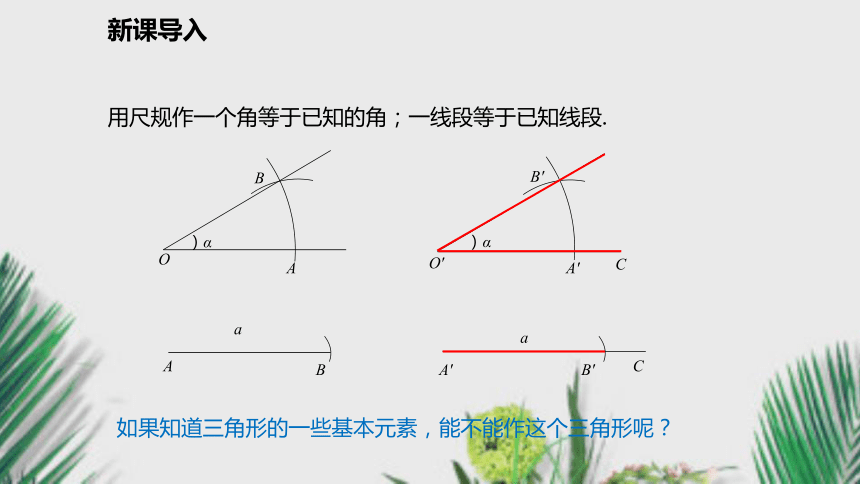
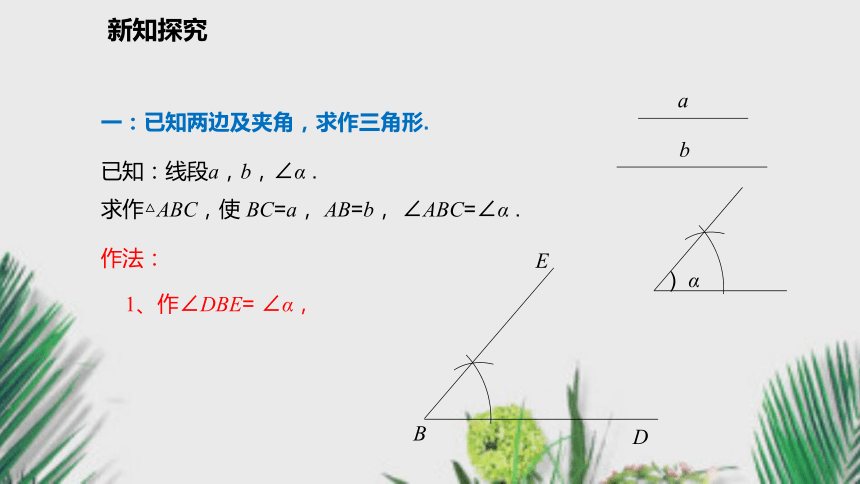
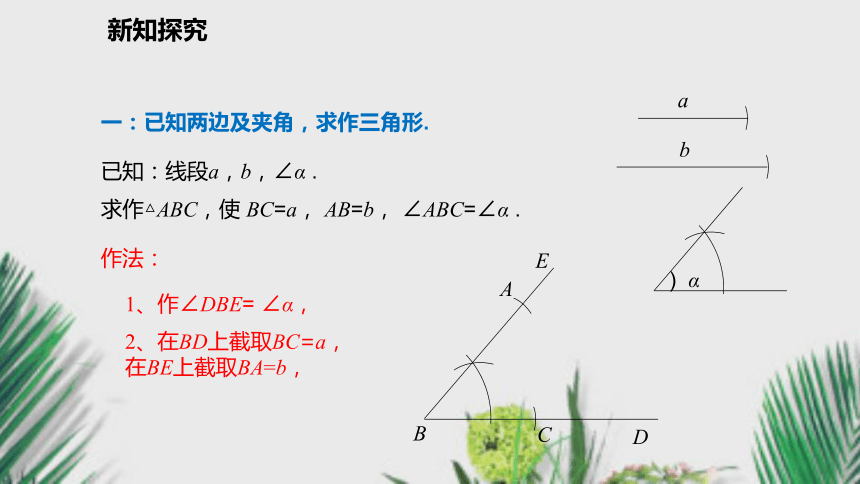
2、在分别给出两角夹边、两边夹角和三边的条件下,能够利用尺规作出三角形.最基本、最常用的尺规作图,通常称为基本作图 .1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知角的角平分线;4、作已知线段的垂直平分线;5、过一点作已知线的垂线.新课导入新课导入用尺规作一个角等于已知的角;一线段等于已知线段.)αOABA′ABB′a)αB′如果知道三角形的一些基本元素,能不能作这个三角形呢?新知探究一:已知两边及夹角,求作三角形.作法:1、作∠DBE= ∠α,E一:已知两边及夹角,求作三角形.作法:1、作∠DBE= ∠α,E2、在BD上截取BC=a,
在BE上截取BA=b,CA新知探究一:已知两边及夹角,求作三角形.作法:1、作∠DBE= ∠α,E2、在BD上截取BC=a,
在BE上截取BA=b,CA3、连接AC,则△ABC就是所求的三角形 .新知探究新知探究回顾刚才作三角形的顺序:夹角边边三角形还有别的画法吗?新知探究二:已知两角及夹边,求作三角形.已知:线段a, ∠ β ,∠α .求作△ABC,使 BC=a, ∠ ACB= ∠ α , ∠ABC= ∠ β .作法:1、作∠EBD=∠β, E新知探究二:已知两角及夹边,求作三角形.已知:线段a, ∠ β ,∠α .求作△ABC,使 BC=a, ∠ ACB= ∠ α , ∠ABC= ∠ β .作法:1、作∠EBD=∠β, E2、作BC=a,C新知探究二:已知两角及夹边,求作三角形.已知:线段a, ∠ β ,∠α .求作△ABC,使 BC=a, ∠ ACB= ∠ α , ∠ABC= ∠ β .作法:1、作∠EBD=∠β, E2、作BC=a,C3、作∠ACB=∠ α,交BE于点A,
则△ABC就是所求作的三角形 .A新知探究回顾刚才作三角形的顺序:角角夹边夹边角角还有没有其他的作法?新知探究已知:线段a,b,c .求作△ABC,使AB=c, BC=a, AC=b .Ba作法:(1)作线段BC=a,
三:已知三边,求作三角形.新知探究已知:线段a,b,c .求作△ABC,使AB=c, BC=a, AC=b .BAabc作法:(1)作线段BC=a,
(2)以B 为圆心,c长为半径作弧;
以C 为圆心,b长为半径作弧,
交前弧于点A .三:已知三边,求作三角形.新知探究已知:线段a,b,c .求作△ABC,使AB=c, BC=a, AC=b .BAabc作法:(1)作线段BC=a;
(2)以B 为圆心,c长为半径作弧;
以C 为圆心,b长为半径作弧,
交前弧于点A ;三:已知三边,求作三角形.(3)则△ABC就是所求作的三角形 .新知探究练习:已知:线段a,c, ∠α,
求作:△ABC,使BC=a,
AB=c, ∠ABC=∠α .ac(步骤:2、在射线BM上截取BC=a,
在射线BN上截取BA=c;3、连接AC,△ABC即为所求作的三角形 .1、作∠MBN= ∠α;MBN?C?A α课堂小结 我们可以利用判断三角形全等的条件(SSS,SAS,ASA)画一个与已知三角形全等的三角形.
在作三角形时,如果已知一角或多个角时,我们通常先画一个角,再画边及其它的角.课堂小测 1.利用尺规不能唯一作出的三角形是( )
A.已知三边
B.已知两边及夹角
C.已知两角及夹边
D.已知两边及其中一边的对角2.利用尺规不可作的直角三角形是( )
A.已知斜边及一条直角边
B.已知两条直角边
C.已知两锐角
D.已知一锐角及一直角边DC课堂小测【解析】依据已知条件,确定作图类型,再依次判断即可.3. 依据尺规作图法,利用已知两个角∠1,∠2及线段a,求作:△ABC,使∠ABC=∠1,∠ACB=∠2,BC=a,则需用的尺规作图的方法有( )
①作一个角等于已知角;②作已知角的角平分线;
③作一条线段等于已知线段;④作已知线段的垂直平分线 .
A. ①②④ B. ①③④ C. ①③ D. ②④解:由已知条件可知,在解答本题的过程中,需先做一条线段BC,
使BC=a,再分别以B,C为顶点,以BC为一边作两个角,使其分别等于∠1和∠2,即可作出所求三角形,故可知需用到的方法为①③ .C
2、在分别给出两角夹边、两边夹角和三边的条件下,能够利用尺规作出三角形.最基本、最常用的尺规作图,通常称为基本作图 .1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知角的角平分线;4、作已知线段的垂直平分线;5、过一点作已知线的垂线.新课导入新课导入用尺规作一个角等于已知的角;一线段等于已知线段.)αOABA′ABB′a)αB′如果知道三角形的一些基本元素,能不能作这个三角形呢?新知探究一:已知两边及夹角,求作三角形.作法:1、作∠DBE= ∠α,E一:已知两边及夹角,求作三角形.作法:1、作∠DBE= ∠α,E2、在BD上截取BC=a,
在BE上截取BA=b,CA新知探究一:已知两边及夹角,求作三角形.作法:1、作∠DBE= ∠α,E2、在BD上截取BC=a,
在BE上截取BA=b,CA3、连接AC,则△ABC就是所求的三角形 .新知探究新知探究回顾刚才作三角形的顺序:夹角边边三角形还有别的画法吗?新知探究二:已知两角及夹边,求作三角形.已知:线段a, ∠ β ,∠α .求作△ABC,使 BC=a, ∠ ACB= ∠ α , ∠ABC= ∠ β .作法:1、作∠EBD=∠β, E新知探究二:已知两角及夹边,求作三角形.已知:线段a, ∠ β ,∠α .求作△ABC,使 BC=a, ∠ ACB= ∠ α , ∠ABC= ∠ β .作法:1、作∠EBD=∠β, E2、作BC=a,C新知探究二:已知两角及夹边,求作三角形.已知:线段a, ∠ β ,∠α .求作△ABC,使 BC=a, ∠ ACB= ∠ α , ∠ABC= ∠ β .作法:1、作∠EBD=∠β, E2、作BC=a,C3、作∠ACB=∠ α,交BE于点A,
则△ABC就是所求作的三角形 .A新知探究回顾刚才作三角形的顺序:角角夹边夹边角角还有没有其他的作法?新知探究已知:线段a,b,c .求作△ABC,使AB=c, BC=a, AC=b .Ba作法:(1)作线段BC=a,
三:已知三边,求作三角形.新知探究已知:线段a,b,c .求作△ABC,使AB=c, BC=a, AC=b .BAabc作法:(1)作线段BC=a,
(2)以B 为圆心,c长为半径作弧;
以C 为圆心,b长为半径作弧,
交前弧于点A .三:已知三边,求作三角形.新知探究已知:线段a,b,c .求作△ABC,使AB=c, BC=a, AC=b .BAabc作法:(1)作线段BC=a;
(2)以B 为圆心,c长为半径作弧;
以C 为圆心,b长为半径作弧,
交前弧于点A ;三:已知三边,求作三角形.(3)则△ABC就是所求作的三角形 .新知探究练习:已知:线段a,c, ∠α,
求作:△ABC,使BC=a,
AB=c, ∠ABC=∠α .ac(步骤:2、在射线BM上截取BC=a,
在射线BN上截取BA=c;3、连接AC,△ABC即为所求作的三角形 .1、作∠MBN= ∠α;MBN?C?A α课堂小结 我们可以利用判断三角形全等的条件(SSS,SAS,ASA)画一个与已知三角形全等的三角形.
在作三角形时,如果已知一角或多个角时,我们通常先画一个角,再画边及其它的角.课堂小测 1.利用尺规不能唯一作出的三角形是( )
A.已知三边
B.已知两边及夹角
C.已知两角及夹边
D.已知两边及其中一边的对角2.利用尺规不可作的直角三角形是( )
A.已知斜边及一条直角边
B.已知两条直角边
C.已知两锐角
D.已知一锐角及一直角边DC课堂小测【解析】依据已知条件,确定作图类型,再依次判断即可.3. 依据尺规作图法,利用已知两个角∠1,∠2及线段a,求作:△ABC,使∠ABC=∠1,∠ACB=∠2,BC=a,则需用的尺规作图的方法有( )
①作一个角等于已知角;②作已知角的角平分线;
③作一条线段等于已知线段;④作已知线段的垂直平分线 .
A. ①②④ B. ①③④ C. ①③ D. ②④解:由已知条件可知,在解答本题的过程中,需先做一条线段BC,
使BC=a,再分别以B,C为顶点,以BC为一边作两个角,使其分别等于∠1和∠2,即可作出所求三角形,故可知需用到的方法为①③ .C
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
