六年级下册数学一课一练-1.2圆柱的表面积 北师大版(含答案)
文档属性
| 名称 | 六年级下册数学一课一练-1.2圆柱的表面积 北师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 66.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-28 09:49:52 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学一课一练-1.2圆柱的表面积
一、单选题
1.做一个无盖的圆柱形铁皮水桶用多少铁皮,就是求(?? )
A.?圆柱体的表面积??????????????????B.?侧面积??????????????????C.?底面积??????????????????D.?侧面积与一个底面积的和
2.把一段长1米,侧面积18.84平方米的圆柱体的木料,沿着和底面平行的方向截成两段,这时它的表面积增加了(?? )
A.?18.84平方米????????????????????B.?28.26平方米????????????????????C.?37.68平方米????????????????????D.?56.52平方米
3.将圆柱体的侧面展开,得不到的是(?? )
A.?平行四边形???????????????????????????????B.?长方形???????????????????????????????C.?梯形???????????????????????????????D.?正方形
二、判断题
4.判断对错
压路机滚动一周能压多少路面是求它的侧面积.
5.两个圆柱的底面积相等,那么它们的体积也相等
6.正方体、长方体和圆柱体的侧面积都可以用底面周长乘高来计算。
?
三、填空题
7.一种圆柱形状的烟囱,底面半径10厘米,高95厘米.做一节这样的烟囱,至少需要________平方厘米的铁皮.(接头处忽略不计)
8.把一个圆柱的侧面展开后,得到一个正方形,这个圆柱的底面半径是5cm,它的高是________cm。
9.一个圆柱的底面直径是4cm,高是1dm,它的表面积是________?cm2 , 体积是________?cm3 .
10.根据所给的条件进行计算.
d=5、h=10(单位:米),求圆柱的表面积是________平方米
11.一台压路机的滚筒宽2米,直径为1.5米.如果它滚动100周,压路的面积是________平方米?
四、解答题
12.做一个无盖的圆柱形铁皮桶,底面直径是40厘米,高5分米,做这个水桶大约用铁皮多少平方厘米?(得数保留整百平方厘米)
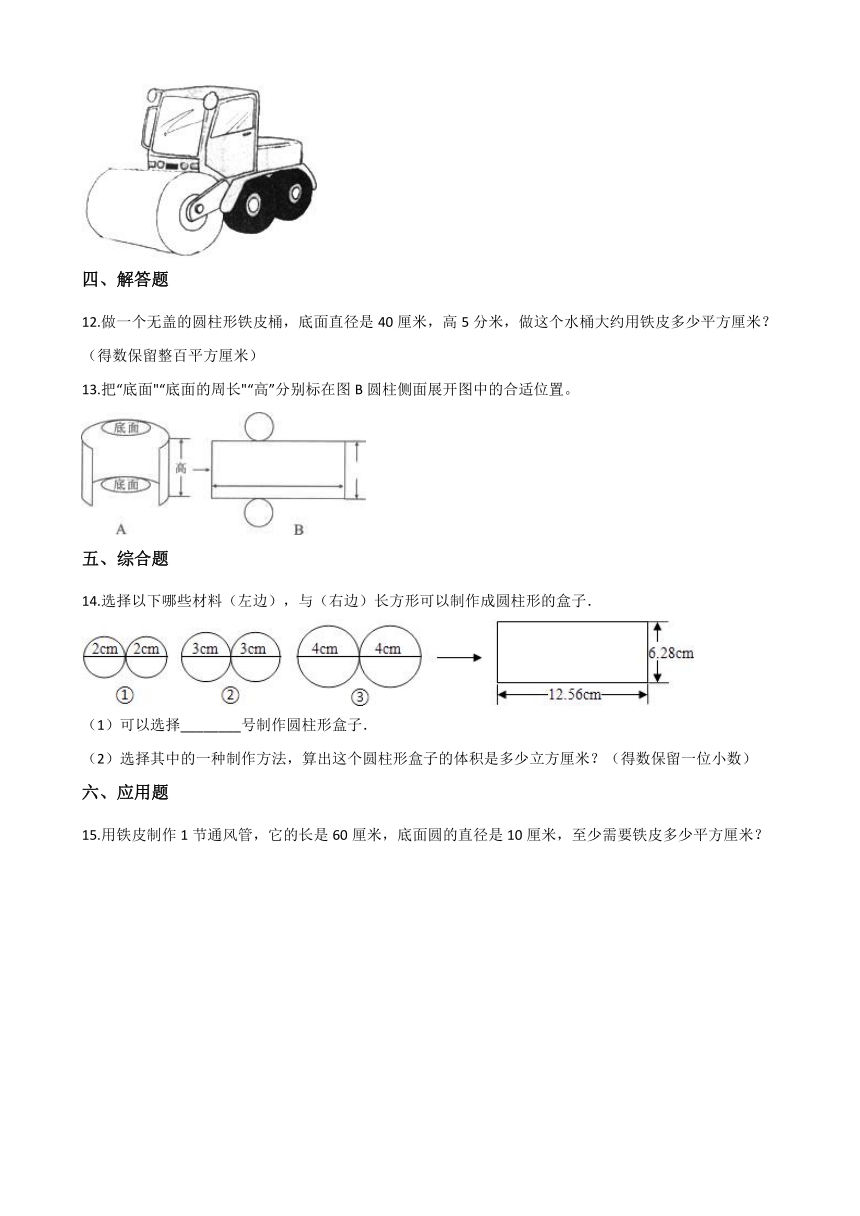
13.把“底面"“底面的周长"“高”分别标在图B圆柱侧面展开图中的合适位置。
五、综合题
14.选择以下哪些材料(左边),与(右边)长方形可以制作成圆柱形的盒子.
(1)可以选择________号制作圆柱形盒子.
(2)选择其中的一种制作方法,算出这个圆柱形盒子的体积是多少立方厘米?(得数保留一位小数)
六、应用题
15.用铁皮制作1节通风管,它的长是60厘米,底面圆的直径是10厘米,至少需要铁皮多少平方厘米?
参考答案
一、单选题
1.【答案】D
【解析】【解答】解:无盖的圆柱形铁皮水桶,只有一个底──侧面积与一个底面积的和是所需铁皮数.
选择D
2.【答案】D
【解析】【解答】18.84÷1=18.84(米)
18.84÷2÷3.14
=9.42÷3.14
=3(米)
3.14×32×2
=3.14×9×2
=28.26×2
=56.52(平方米)
故答案为:D.
【分析】将一个圆柱体的木料,沿着和底面平行的方向截成两段,这时它的表面积增加了两个底面积,已知圆柱的侧面积和高,求底面周长,用圆柱的侧面积÷高=底面周长,然后用底面周长÷2÷π=底面半径,最后用公式:S=πr2求出圆柱的底面积,再乘2即可解答.
3.【答案】 C
【解析】【解答】解:将圆柱的侧面斜着剪开后得到平行四边形;将侧面沿着一条高剪开后得到一个长方形或正方形;如何剪都不会得到一个梯形.
故答案为:C
【分析】圆柱的侧面展开后是一个平面图形,剪开的方法不同,呈现的形状就不同,可能会得到长方形、正方形或平行四边形,但不会得到梯形.
二、判断题
4.【答案】 正确
【解析】【解答】解:压路机滚动一周能压到的路面,实际上就是圆柱形的压路机的侧面展开图,因此求滚动一周能压过的路面,就是求它的侧面积.
5.【答案】错误
【解析】【解答】因为圆柱的体积=底面积×高,虽然两个圆柱的底面积相等,但高不一定相等,所以它们的体积也相等是错误的。
故答案为:错误
【分析】圆柱的体积与圆柱的底面积和圆柱的高两个条件有关系,单独的一个条件不能确定圆柱的体积,由此判断即可。
6.【答案】正确
【解析】【解答】正方体、长方体和圆柱体的侧面积都可以用底面周长乘高来计算正确。
【分析】正方体、长方体和圆柱体的侧面积都可以用底面周长乘高来计算,圆锥的侧面积不能用此计算。
三、填空题
7.【答案】 5966
【解析】【解答】2×3.14×10×95
=62.8×95
=5966(平方厘米)
答:至少需要5966平方厘米铁皮。
【分析】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
8.【答案】31.4
【解析】【解答】解:3.14×5×2=31.4(cm)
故答案为:31.4
【分析】圆柱的侧面展开后是一个正方形,那么这个圆柱的底面周长和高相等,由此根据圆周长公式计算即可.
9.【答案】 150.72;125.6
【解析】【解答】解:1分米=10厘米,
3.14×4×10+3.14×(4÷2)2×2
=125.6+3.14×4×2
=125.6+12.56×2
=125.6+25.12
=150.72(平方厘米);
3.14×(4÷2)2×10
=3.14×4×10
=12.56×10
=125.6(立方厘米);
答:这个圆柱的表面积是150.72平方厘米,体积是125.6立方厘米.
故答案为:150.72;125.6.
【分析】根据圆柱的表面积公式、体积公式,圆柱的表面积=侧面积+底面积×2,圆柱的体积=底面积×高,把数据分别代入公式解答即可.
10.【答案】196.25
【解析】【解答】3.14×5×10+3.14×(5÷2)2×2
=3.14×5×10+3.14×2.52×2
=15.7×10+3.14×6.25×2
=157+19.625×2
=157+39.25
=196.25(平方米)
故答案为:196.25
【分析】已知圆柱的底面直径和高,求圆柱的表面积,用公式:S=πdh+π(d÷2)2×2,据此列式解答.
11.【答案】942
【解析】【解答】3.14×1.5×2×100
=3.14×300
=942(平方米)
故答案为:942
【分析】用底面周长乘滚筒的宽求出滚筒的侧面积,用侧面积乘100即可求出压路的总面积.
四、解答题
12.【答案】 解:5分米=50厘米
3.14×(40÷2)2+3.14×40×50
=3.14×400+3.14×2000
=3.14×2400
=7536(平方厘米)
≈7600(平方厘米)
答:做这个水桶大约需用7600平方厘米铁皮
【解析】【分析】因要做的水桶无盖,需要求的就是水桶的一个底面积和侧面积的和,根据圆的面积公式:S=π(d÷2)2可求出底面积,再根据圆柱的侧面积=底面周长×高可求出侧面积,据此解答.本题主要考查了学生对圆柱底面积和侧面积计算方法的掌握.
13.【答案】解:如图:
【解析】【分析】圆柱展开后会得到两个相同的圆形和一个长方形,这个长方形就是圆柱的侧面展开图,长方形的长与圆柱的底面周长相等,宽就是圆柱的高.
五、综合题
14.【答案】(1)①或③
(2)解:选择③号制作的盒子的体积是:
3.14×(4÷2)2×6.28,
=3.14×4×6.28,
=12.56×6.28,
=78.8768(立方厘米),
≈78.9(立方厘米);
答:可以选择①或③号制作圆柱形盒子;选择③号制作的盒子的体积是78.9立方厘米.
【解析】【解答】解:(1)因为①号的周长是:3.14×2=6.28(厘米),
等于右边材料的宽,所以可以选①号和长方形搭配;
又因③号的周长是:3.14×4=12.56(厘米);
则等于右边材料的长;所以也可以应选择③号和长方形搭配;
(2)选择③号制作的盒子的体积是:
3.14×(4÷2)2×6.28,
=3.14×4×6.28,
=12.56×6.28,
=78.8768(立方厘米),
≈78.9(立方厘米);
答:可以选择①或③号制作圆柱形盒子;选择③号制作的盒子的体积是78.9立方厘米.
故答案为:①或③.
【分析】(1)由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高,据此即可计算长方形的长与圆形的底面周长,若相等,则可以选择,否则不能选择;(2)求盒子的体积可以利用圆柱的体积公式,即圆柱的体积=底面积×高,将数据分别代入公式即可求其体积.解答此题的关键是明白:长方形的长或宽与圆形的底面周长,若相等,则可以选择,否则不能选择.
六、应用题
15.【答案】解:3.14×10×60=1884(平方厘米)
答:至少需要铁皮1884平方厘米。
【解析】【分析】此题考查了圆柱的侧面积公式的计算应用,此类问题要结合生活实际,此题就是求这个底面直径为10厘米,长60厘米的圆柱的侧面积,由此利用圆柱的侧面积=底面周长×高即可计算。
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学一课一练-1.2圆柱的表面积
一、单选题
1.做一个无盖的圆柱形铁皮水桶用多少铁皮,就是求(?? )
A.?圆柱体的表面积??????????????????B.?侧面积??????????????????C.?底面积??????????????????D.?侧面积与一个底面积的和
2.把一段长1米,侧面积18.84平方米的圆柱体的木料,沿着和底面平行的方向截成两段,这时它的表面积增加了(?? )
A.?18.84平方米????????????????????B.?28.26平方米????????????????????C.?37.68平方米????????????????????D.?56.52平方米
3.将圆柱体的侧面展开,得不到的是(?? )
A.?平行四边形???????????????????????????????B.?长方形???????????????????????????????C.?梯形???????????????????????????????D.?正方形
二、判断题
4.判断对错
压路机滚动一周能压多少路面是求它的侧面积.
5.两个圆柱的底面积相等,那么它们的体积也相等
6.正方体、长方体和圆柱体的侧面积都可以用底面周长乘高来计算。
?
三、填空题
7.一种圆柱形状的烟囱,底面半径10厘米,高95厘米.做一节这样的烟囱,至少需要________平方厘米的铁皮.(接头处忽略不计)
8.把一个圆柱的侧面展开后,得到一个正方形,这个圆柱的底面半径是5cm,它的高是________cm。
9.一个圆柱的底面直径是4cm,高是1dm,它的表面积是________?cm2 , 体积是________?cm3 .
10.根据所给的条件进行计算.
d=5、h=10(单位:米),求圆柱的表面积是________平方米
11.一台压路机的滚筒宽2米,直径为1.5米.如果它滚动100周,压路的面积是________平方米?
四、解答题
12.做一个无盖的圆柱形铁皮桶,底面直径是40厘米,高5分米,做这个水桶大约用铁皮多少平方厘米?(得数保留整百平方厘米)
13.把“底面"“底面的周长"“高”分别标在图B圆柱侧面展开图中的合适位置。
五、综合题
14.选择以下哪些材料(左边),与(右边)长方形可以制作成圆柱形的盒子.
(1)可以选择________号制作圆柱形盒子.
(2)选择其中的一种制作方法,算出这个圆柱形盒子的体积是多少立方厘米?(得数保留一位小数)
六、应用题
15.用铁皮制作1节通风管,它的长是60厘米,底面圆的直径是10厘米,至少需要铁皮多少平方厘米?
参考答案
一、单选题
1.【答案】D
【解析】【解答】解:无盖的圆柱形铁皮水桶,只有一个底──侧面积与一个底面积的和是所需铁皮数.
选择D
2.【答案】D
【解析】【解答】18.84÷1=18.84(米)
18.84÷2÷3.14
=9.42÷3.14
=3(米)
3.14×32×2
=3.14×9×2
=28.26×2
=56.52(平方米)
故答案为:D.
【分析】将一个圆柱体的木料,沿着和底面平行的方向截成两段,这时它的表面积增加了两个底面积,已知圆柱的侧面积和高,求底面周长,用圆柱的侧面积÷高=底面周长,然后用底面周长÷2÷π=底面半径,最后用公式:S=πr2求出圆柱的底面积,再乘2即可解答.
3.【答案】 C
【解析】【解答】解:将圆柱的侧面斜着剪开后得到平行四边形;将侧面沿着一条高剪开后得到一个长方形或正方形;如何剪都不会得到一个梯形.
故答案为:C
【分析】圆柱的侧面展开后是一个平面图形,剪开的方法不同,呈现的形状就不同,可能会得到长方形、正方形或平行四边形,但不会得到梯形.
二、判断题
4.【答案】 正确
【解析】【解答】解:压路机滚动一周能压到的路面,实际上就是圆柱形的压路机的侧面展开图,因此求滚动一周能压过的路面,就是求它的侧面积.
5.【答案】错误
【解析】【解答】因为圆柱的体积=底面积×高,虽然两个圆柱的底面积相等,但高不一定相等,所以它们的体积也相等是错误的。
故答案为:错误
【分析】圆柱的体积与圆柱的底面积和圆柱的高两个条件有关系,单独的一个条件不能确定圆柱的体积,由此判断即可。
6.【答案】正确
【解析】【解答】正方体、长方体和圆柱体的侧面积都可以用底面周长乘高来计算正确。
【分析】正方体、长方体和圆柱体的侧面积都可以用底面周长乘高来计算,圆锥的侧面积不能用此计算。
三、填空题
7.【答案】 5966
【解析】【解答】2×3.14×10×95
=62.8×95
=5966(平方厘米)
答:至少需要5966平方厘米铁皮。
【分析】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
8.【答案】31.4
【解析】【解答】解:3.14×5×2=31.4(cm)
故答案为:31.4
【分析】圆柱的侧面展开后是一个正方形,那么这个圆柱的底面周长和高相等,由此根据圆周长公式计算即可.
9.【答案】 150.72;125.6
【解析】【解答】解:1分米=10厘米,
3.14×4×10+3.14×(4÷2)2×2
=125.6+3.14×4×2
=125.6+12.56×2
=125.6+25.12
=150.72(平方厘米);
3.14×(4÷2)2×10
=3.14×4×10
=12.56×10
=125.6(立方厘米);
答:这个圆柱的表面积是150.72平方厘米,体积是125.6立方厘米.
故答案为:150.72;125.6.
【分析】根据圆柱的表面积公式、体积公式,圆柱的表面积=侧面积+底面积×2,圆柱的体积=底面积×高,把数据分别代入公式解答即可.
10.【答案】196.25
【解析】【解答】3.14×5×10+3.14×(5÷2)2×2
=3.14×5×10+3.14×2.52×2
=15.7×10+3.14×6.25×2
=157+19.625×2
=157+39.25
=196.25(平方米)
故答案为:196.25
【分析】已知圆柱的底面直径和高,求圆柱的表面积,用公式:S=πdh+π(d÷2)2×2,据此列式解答.
11.【答案】942
【解析】【解答】3.14×1.5×2×100
=3.14×300
=942(平方米)
故答案为:942
【分析】用底面周长乘滚筒的宽求出滚筒的侧面积,用侧面积乘100即可求出压路的总面积.
四、解答题
12.【答案】 解:5分米=50厘米
3.14×(40÷2)2+3.14×40×50
=3.14×400+3.14×2000
=3.14×2400
=7536(平方厘米)
≈7600(平方厘米)
答:做这个水桶大约需用7600平方厘米铁皮
【解析】【分析】因要做的水桶无盖,需要求的就是水桶的一个底面积和侧面积的和,根据圆的面积公式:S=π(d÷2)2可求出底面积,再根据圆柱的侧面积=底面周长×高可求出侧面积,据此解答.本题主要考查了学生对圆柱底面积和侧面积计算方法的掌握.
13.【答案】解:如图:
【解析】【分析】圆柱展开后会得到两个相同的圆形和一个长方形,这个长方形就是圆柱的侧面展开图,长方形的长与圆柱的底面周长相等,宽就是圆柱的高.
五、综合题
14.【答案】(1)①或③
(2)解:选择③号制作的盒子的体积是:
3.14×(4÷2)2×6.28,
=3.14×4×6.28,
=12.56×6.28,
=78.8768(立方厘米),
≈78.9(立方厘米);
答:可以选择①或③号制作圆柱形盒子;选择③号制作的盒子的体积是78.9立方厘米.
【解析】【解答】解:(1)因为①号的周长是:3.14×2=6.28(厘米),
等于右边材料的宽,所以可以选①号和长方形搭配;
又因③号的周长是:3.14×4=12.56(厘米);
则等于右边材料的长;所以也可以应选择③号和长方形搭配;
(2)选择③号制作的盒子的体积是:
3.14×(4÷2)2×6.28,
=3.14×4×6.28,
=12.56×6.28,
=78.8768(立方厘米),
≈78.9(立方厘米);
答:可以选择①或③号制作圆柱形盒子;选择③号制作的盒子的体积是78.9立方厘米.
故答案为:①或③.
【分析】(1)由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高,据此即可计算长方形的长与圆形的底面周长,若相等,则可以选择,否则不能选择;(2)求盒子的体积可以利用圆柱的体积公式,即圆柱的体积=底面积×高,将数据分别代入公式即可求其体积.解答此题的关键是明白:长方形的长或宽与圆形的底面周长,若相等,则可以选择,否则不能选择.
六、应用题
15.【答案】解:3.14×10×60=1884(平方厘米)
答:至少需要铁皮1884平方厘米。
【解析】【分析】此题考查了圆柱的侧面积公式的计算应用,此类问题要结合生活实际,此题就是求这个底面直径为10厘米,长60厘米的圆柱的侧面积,由此利用圆柱的侧面积=底面周长×高即可计算。
