沪科版八年级数学下册课件17.5.1面积问题与数字问题(23张)
文档属性
| 名称 | 沪科版八年级数学下册课件17.5.1面积问题与数字问题(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-28 00:00:00 | ||
图片预览





文档简介
课件23张PPT。第十七章
一元二次方程八年级数学沪科版·下册 17.5.1面积问题与数字问题新课引入
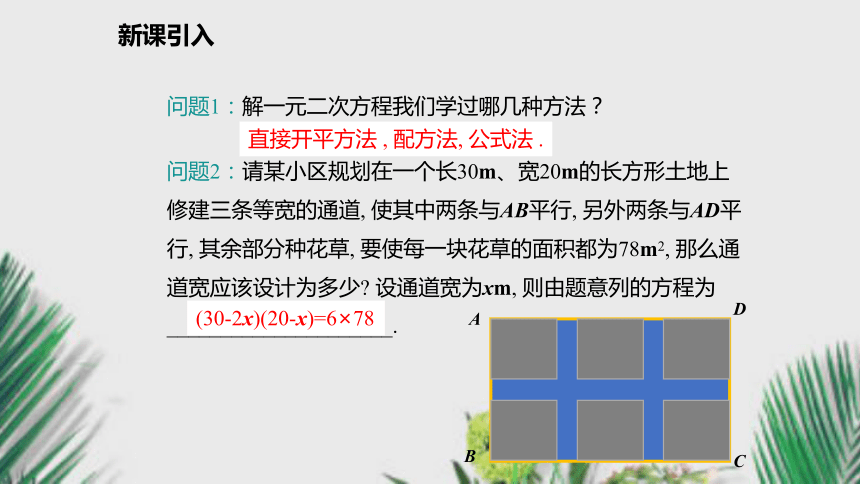
问题1:解一元二次方程我们学过哪几种方法?直接开平方法?, 配方法, 公式法 .问题2:请某小区规划在一个长30m、宽20m的长方形土地上修建三条等宽的通道, 使其中两条与AB平行, 另外两条与AD平行, 其余部分种花草, 要使每一块花草的面积都为78m2, 那么通道宽应该设计为多少? 设通道宽为xm, 则由题意列的方程为_____________________.(30-2x)(20-x)=6×78新知探究
问题:在一块长16m, 宽12m的矩形荒地上, 要建造上个花园, 并
使花园所占面积为荒地面积的一半.想一想,你会怎么设计这片荒地?看一看:下面几位同学的设计方法是否合理?新知探究
解:设小路的宽为 x m, 根据题意得:
即 x2 - 14x + 24 = 0.
解方程得 x1 = 2 , x2 = 12.
将x = 12 代入方程中不符合题意舍去.
答:小路的宽为2m.小明设计:
如图所示. 其中花园四周小路的宽都相等. 通过解方程,
得到小路的宽为2m或12m.问题:你觉得他的结果对吗?你能将小明的解答过程重现吗?xx新知探究
解:设扇形半径为 x m, 根据题意得:
即 πx2 = 96.
解方程得 x1 = , x2 = (舍去).
答: 扇形半径约为5.5m.小亮设计:
如图所示. 其中花园每个角上的扇形都相同.问题:你能帮小亮计算一下这个扇形的半径是多少吗?新知探究 小颖设计:
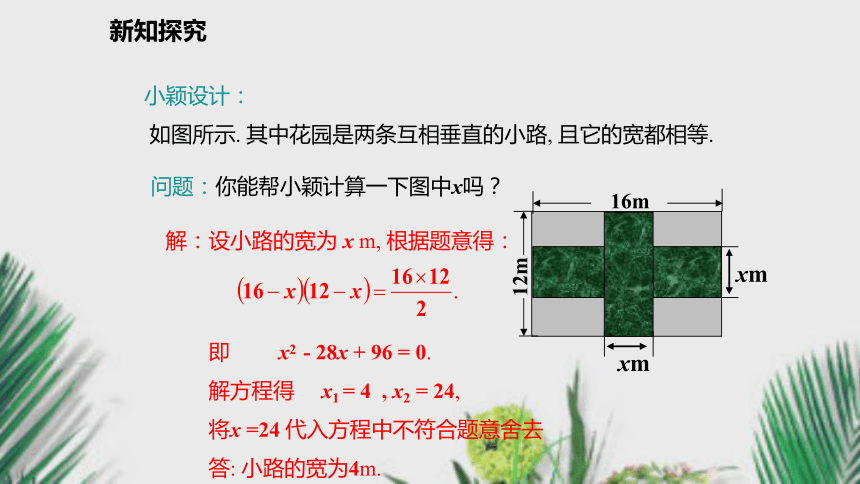
如图所示. 其中花园是两条互相垂直的小路, 且它的宽都相等.问题:你能帮小颖计算一下图中x吗?解:设小路的宽为 x m, 根据题意得:
即 x2 - 28x + 96 = 0.
解方程得 x1 = 4 , x2 = 24,
将x =24 代入方程中不符合题意舍去
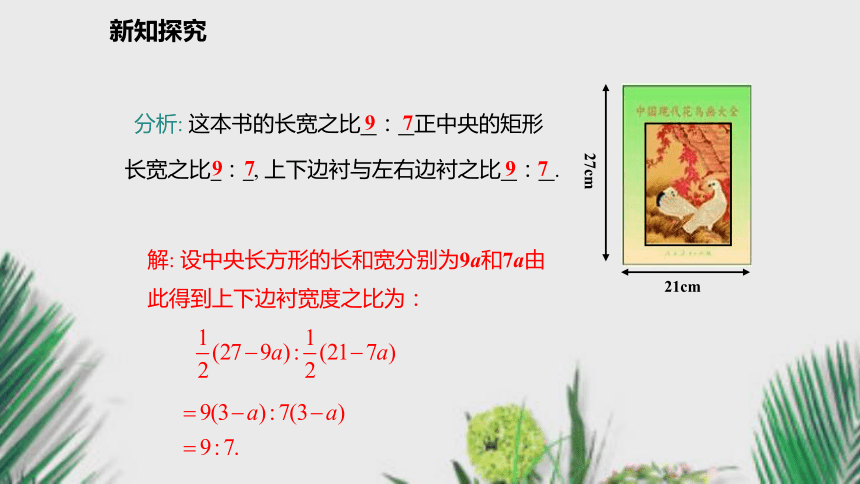
答: 小路的宽为4m.新知探究 例1 要设计一本书的封面, 封面长27cm, 宽21cm正中央是一个与整个封面长宽比例相同的矩形, 如果要使四周的边衬所占面积是封面面积的四分之一, 上、下边衬等宽, 左、右边衬等宽, 应如何设计四周边衬的宽度?(精确到0.1cm)27cm21cm新知探究 分析: 这本书的长宽之比 : 正中央的矩形长宽之比 : , 上下边衬与左右边衬之比 : .9 79 727cm21cm解: 设中央长方形的长和宽分别为9a和7a由
此得到上下边衬宽度之比为:9 7新知探究27cm21cm 解: 设上下边衬的9xcm, 左右边衬宽为7xcm依题意得解方程得故上下边衬的宽度为故左右边衬的宽度为答: 上下边衬的宽度为1.8cm, 左右边衬的宽度为1.4cm.
解法一新知探究 解: 设正中央的矩形两边别为9xcm, 7xcm. 依题意得27cm21cm解得 故上下边衬的宽度为故左右边衬的宽度为解法二新知探究 (1)主要集中在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形, 找出各部分面积之间的关系, 再运用规则图形的面积公式列出方程;
(2)与直角三角形有关的问题: 直角三角形两直角边的平方和等于斜边的平方是这类问题的等量关系, 即用勾股定理列方程.新知探究例2 如图, 在一块长为 92m , 宽为 60m 的矩形耕地上挖三条水渠, 水渠的宽都相等, 水渠把耕地分成面积均为 885m2 的 6 个矩形小块, 水渠应挖多宽? 分析: 设水渠宽为xm, 将所有耕地的面积拼在一起, 变成一个新的矩形, 长为 (92 – 2x )m, 宽(60 - x)m.
解: 设水渠的宽应挖 x m .
( 92 - 2x)(60 - x )= 6×885.解得 x1=105(舍去), x2=1.新知探究 我们利用“图形经过移动, 它的面积大小不会改变”的性质, 把纵、横两条路移动一下, 使列方程容易些(目的是求出水渠的宽, 至于实际施工, 仍可按原图的位置修路).新知探究问1:连续三个奇数, 若第一个为x, 则后2个为 .x+2, x+4问2:连续的五个整数, 若中间一个数位n,
其余的为 .n+2, n+1, n-1, n-2问3:一个两位数, 十位数字为a, 个位数字为b,
则这个两位是 .10a+b问4:一个三位数, 百位x, 十位y, 个位z, 表示为 .100x+10y+z新知探究例1 两个连续奇数的积为63, 求这个两个数.解: 设两个奇数为x 和 x+2.x(x+2)=63?x1=-9, x2=7.x1+2=-7, x2+2=9.答: 这个两个数为7, 9, 或者-7, -9.新知探究练习: 三个连续整数, 两两之积的和为587, 求这三个数.解: 设这三个连续整数为x-1, x, x+1, (x-1)x+(x-1)(x+1)+x(x+1)=587?x1-1 = 13
x1+1= 15x2-1= -15
x2+1= -13 答: 这三个数为13, 14, 15 或 -13, -14, -15.新知探究例2 一个两位数, 十位数字与个位数字之和为5, 把这个数的个位数字与十位数字对调后, 所得的新数与两位数之积为736, 求这个两位数.分析: 设原来的两位数个位数字为x, 则十位数字为(5-x).十位 个位 两位数原两位数新两位数5-x5-x x x10(5-x)+ x10x + 5-x 如图是宽为20米, 长为32米的矩形耕地, 要修筑同样宽的三条道路(两条纵向, 一条横向, 且互相垂直), 把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米, 问: 道路宽为多少米?解:设道路宽为x米, 则 化简得,其中的 x=35超出了原矩形的宽, 应舍去.答: 道路的宽为1米.新知探究课堂小结利用一元二次方程解决面积问题 几何图形常见几何图形面积是等量关系. 类 型花坛面积问题相框宽度问题常采用图形平移能聚零为整方便列方程课堂小测1.在一幅长90cm, 宽40cm的风景画四周外围镶上一条宽度相同的金色纸边, 制成一幅挂图. 如果要求风景画的面积是整个挂图面积的72%. 那么金边的宽应是多少?解: 设金边的宽为 x cm, 根据题意得
(90 + 2x)(40 + 2x)×72% = 90×40,
即 x2 + 65x - 350 = 0.
解方程, 得
x1= 5 , x2 = -70 (舍去).
答: 金边的宽应是5cm.课堂小测2. 某农场要建一个长方形的养鸡场, 养鸡场的一边靠墙(墙长25m),
另外三边用木栏围成, 木栏长40m.(1) 养鸡场的面积能达到180m2吗?
如果能, 请给出设计方案; 如果不能,
请说明理由.解: 设养鸡场的长为 x m,根据题意得
即 x2 - 40x + 360=0.
解方程, 得 x1 = , x2= (舍去),
答:鸡场的长为( )m满足条件.x课堂小测3. 如图1, 在宽为20米, 长为32米的矩形地面上修筑同样宽的道路(图中阴影部分), 余下的部分种上草坪. 要使草坪的面积为540平方米, 求道路的宽. 解: 设道路宽为 x 米, 由平移得到图2, 则宽为(20-x)米, 长为(32-x)米, 列方程得 (20-x)(32-x)=540,整理得 x2-52x+100=0,解得 x1=50(舍去), x2=2.答: 道路宽为2米.课堂小测4. 一个两位数等于个位数字与十位数字之积的3倍,
其十位数字比个位数字小2, 求这个两位数.?
问题1:解一元二次方程我们学过哪几种方法?直接开平方法?, 配方法, 公式法 .问题2:请某小区规划在一个长30m、宽20m的长方形土地上修建三条等宽的通道, 使其中两条与AB平行, 另外两条与AD平行, 其余部分种花草, 要使每一块花草的面积都为78m2, 那么通道宽应该设计为多少? 设通道宽为xm, 则由题意列的方程为_____________________.(30-2x)(20-x)=6×78新知探究
问题:在一块长16m, 宽12m的矩形荒地上, 要建造上个花园, 并
使花园所占面积为荒地面积的一半.想一想,你会怎么设计这片荒地?看一看:下面几位同学的设计方法是否合理?新知探究
解:设小路的宽为 x m, 根据题意得:
即 x2 - 14x + 24 = 0.
解方程得 x1 = 2 , x2 = 12.
将x = 12 代入方程中不符合题意舍去.
答:小路的宽为2m.小明设计:
如图所示. 其中花园四周小路的宽都相等. 通过解方程,
得到小路的宽为2m或12m.问题:你觉得他的结果对吗?你能将小明的解答过程重现吗?xx新知探究
解:设扇形半径为 x m, 根据题意得:
即 πx2 = 96.
解方程得 x1 = , x2 = (舍去).
答: 扇形半径约为5.5m.小亮设计:
如图所示. 其中花园每个角上的扇形都相同.问题:你能帮小亮计算一下这个扇形的半径是多少吗?新知探究 小颖设计:
如图所示. 其中花园是两条互相垂直的小路, 且它的宽都相等.问题:你能帮小颖计算一下图中x吗?解:设小路的宽为 x m, 根据题意得:
即 x2 - 28x + 96 = 0.
解方程得 x1 = 4 , x2 = 24,
将x =24 代入方程中不符合题意舍去
答: 小路的宽为4m.新知探究 例1 要设计一本书的封面, 封面长27cm, 宽21cm正中央是一个与整个封面长宽比例相同的矩形, 如果要使四周的边衬所占面积是封面面积的四分之一, 上、下边衬等宽, 左、右边衬等宽, 应如何设计四周边衬的宽度?(精确到0.1cm)27cm21cm新知探究 分析: 这本书的长宽之比 : 正中央的矩形长宽之比 : , 上下边衬与左右边衬之比 : .9 79 727cm21cm解: 设中央长方形的长和宽分别为9a和7a由
此得到上下边衬宽度之比为:9 7新知探究27cm21cm 解: 设上下边衬的9xcm, 左右边衬宽为7xcm依题意得解方程得故上下边衬的宽度为故左右边衬的宽度为答: 上下边衬的宽度为1.8cm, 左右边衬的宽度为1.4cm.
解法一新知探究 解: 设正中央的矩形两边别为9xcm, 7xcm. 依题意得27cm21cm解得 故上下边衬的宽度为故左右边衬的宽度为解法二新知探究 (1)主要集中在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形, 找出各部分面积之间的关系, 再运用规则图形的面积公式列出方程;
(2)与直角三角形有关的问题: 直角三角形两直角边的平方和等于斜边的平方是这类问题的等量关系, 即用勾股定理列方程.新知探究例2 如图, 在一块长为 92m , 宽为 60m 的矩形耕地上挖三条水渠, 水渠的宽都相等, 水渠把耕地分成面积均为 885m2 的 6 个矩形小块, 水渠应挖多宽? 分析: 设水渠宽为xm, 将所有耕地的面积拼在一起, 变成一个新的矩形, 长为 (92 – 2x )m, 宽(60 - x)m.
解: 设水渠的宽应挖 x m .
( 92 - 2x)(60 - x )= 6×885.解得 x1=105(舍去), x2=1.新知探究 我们利用“图形经过移动, 它的面积大小不会改变”的性质, 把纵、横两条路移动一下, 使列方程容易些(目的是求出水渠的宽, 至于实际施工, 仍可按原图的位置修路).新知探究问1:连续三个奇数, 若第一个为x, 则后2个为 .x+2, x+4问2:连续的五个整数, 若中间一个数位n,
其余的为 .n+2, n+1, n-1, n-2问3:一个两位数, 十位数字为a, 个位数字为b,
则这个两位是 .10a+b问4:一个三位数, 百位x, 十位y, 个位z, 表示为 .100x+10y+z新知探究例1 两个连续奇数的积为63, 求这个两个数.解: 设两个奇数为x 和 x+2.x(x+2)=63?x1=-9, x2=7.x1+2=-7, x2+2=9.答: 这个两个数为7, 9, 或者-7, -9.新知探究练习: 三个连续整数, 两两之积的和为587, 求这三个数.解: 设这三个连续整数为x-1, x, x+1, (x-1)x+(x-1)(x+1)+x(x+1)=587?x1-1 = 13
x1+1= 15x2-1= -15
x2+1= -13 答: 这三个数为13, 14, 15 或 -13, -14, -15.新知探究例2 一个两位数, 十位数字与个位数字之和为5, 把这个数的个位数字与十位数字对调后, 所得的新数与两位数之积为736, 求这个两位数.分析: 设原来的两位数个位数字为x, 则十位数字为(5-x).十位 个位 两位数原两位数新两位数5-x5-x x x10(5-x)+ x10x + 5-x 如图是宽为20米, 长为32米的矩形耕地, 要修筑同样宽的三条道路(两条纵向, 一条横向, 且互相垂直), 把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米, 问: 道路宽为多少米?解:设道路宽为x米, 则 化简得,其中的 x=35超出了原矩形的宽, 应舍去.答: 道路的宽为1米.新知探究课堂小结利用一元二次方程解决面积问题 几何图形常见几何图形面积是等量关系. 类 型花坛面积问题相框宽度问题常采用图形平移能聚零为整方便列方程课堂小测1.在一幅长90cm, 宽40cm的风景画四周外围镶上一条宽度相同的金色纸边, 制成一幅挂图. 如果要求风景画的面积是整个挂图面积的72%. 那么金边的宽应是多少?解: 设金边的宽为 x cm, 根据题意得
(90 + 2x)(40 + 2x)×72% = 90×40,
即 x2 + 65x - 350 = 0.
解方程, 得
x1= 5 , x2 = -70 (舍去).
答: 金边的宽应是5cm.课堂小测2. 某农场要建一个长方形的养鸡场, 养鸡场的一边靠墙(墙长25m),
另外三边用木栏围成, 木栏长40m.(1) 养鸡场的面积能达到180m2吗?
如果能, 请给出设计方案; 如果不能,
请说明理由.解: 设养鸡场的长为 x m,根据题意得
即 x2 - 40x + 360=0.
解方程, 得 x1 = , x2= (舍去),
答:鸡场的长为( )m满足条件.x课堂小测3. 如图1, 在宽为20米, 长为32米的矩形地面上修筑同样宽的道路(图中阴影部分), 余下的部分种上草坪. 要使草坪的面积为540平方米, 求道路的宽. 解: 设道路宽为 x 米, 由平移得到图2, 则宽为(20-x)米, 长为(32-x)米, 列方程得 (20-x)(32-x)=540,整理得 x2-52x+100=0,解得 x1=50(舍去), x2=2.答: 道路宽为2米.课堂小测4. 一个两位数等于个位数字与十位数字之积的3倍,
其十位数字比个位数字小2, 求这个两位数.?
