25.2.1 三视图的定义及画法(自主预习+课后集训+答案)
文档属性
| 名称 | 25.2.1 三视图的定义及画法(自主预习+课后集训+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版数学九年级下册同步课时训练
第25章
投影与视图
25.2 三视图
第1课时 三视图的定义及画法
要点测评
基础达标
要点1 三视图的概念、特征及画法
1.
由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有(
)
A.
1个
B.
2个
C.
3个
D.
4个
2.
如图,在常见的几何体圆锥,圆柱,球,长方体中,主视图与它的左视图一定完全相同的几何体有
(填编号).
3.
由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图.且使该主视图是轴对称图形.
要点2 三视图与立体图形的关系
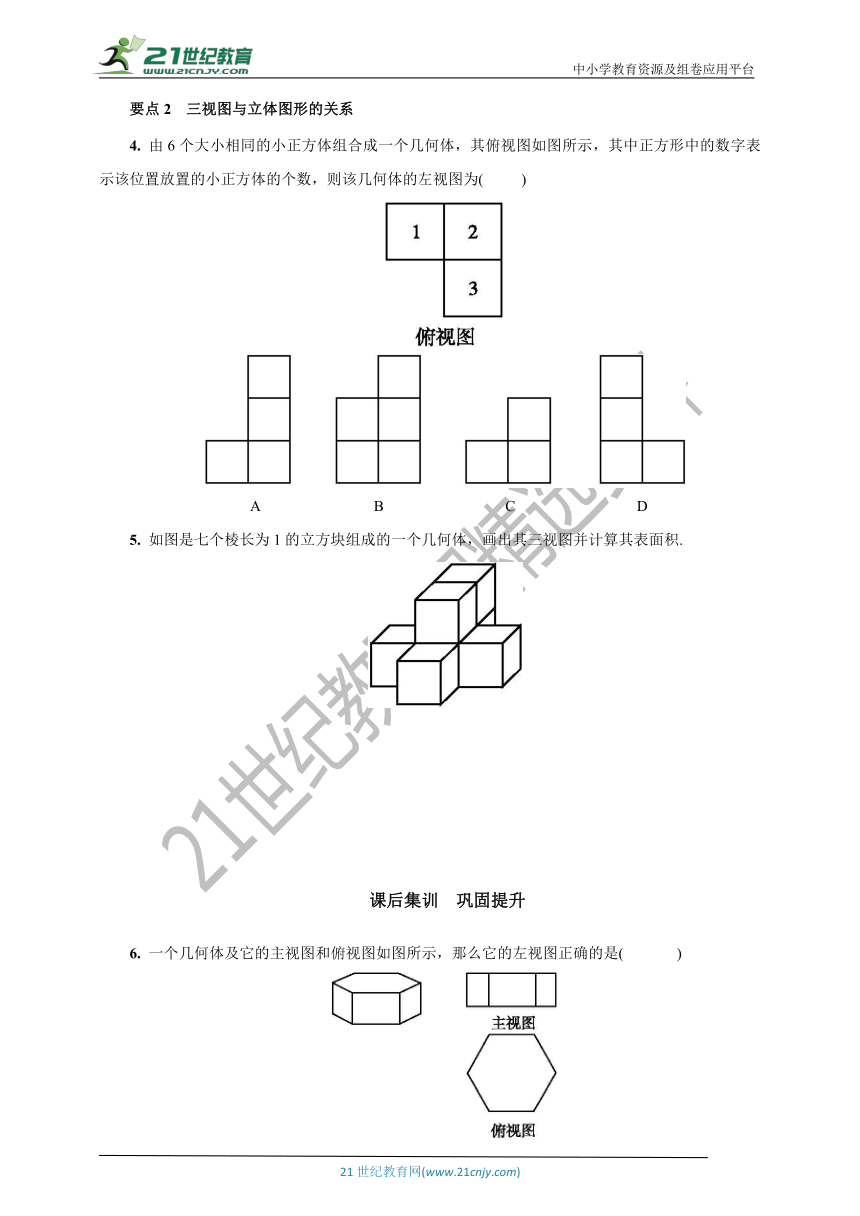
4.
由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为(
)
A
B
C
D
5.
如图是七个棱长为1的立方块组成的一个几何体,画出其三视图并计算其表面积.
课后集训
巩固提升
6.
一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是(
)
A
B
C
D
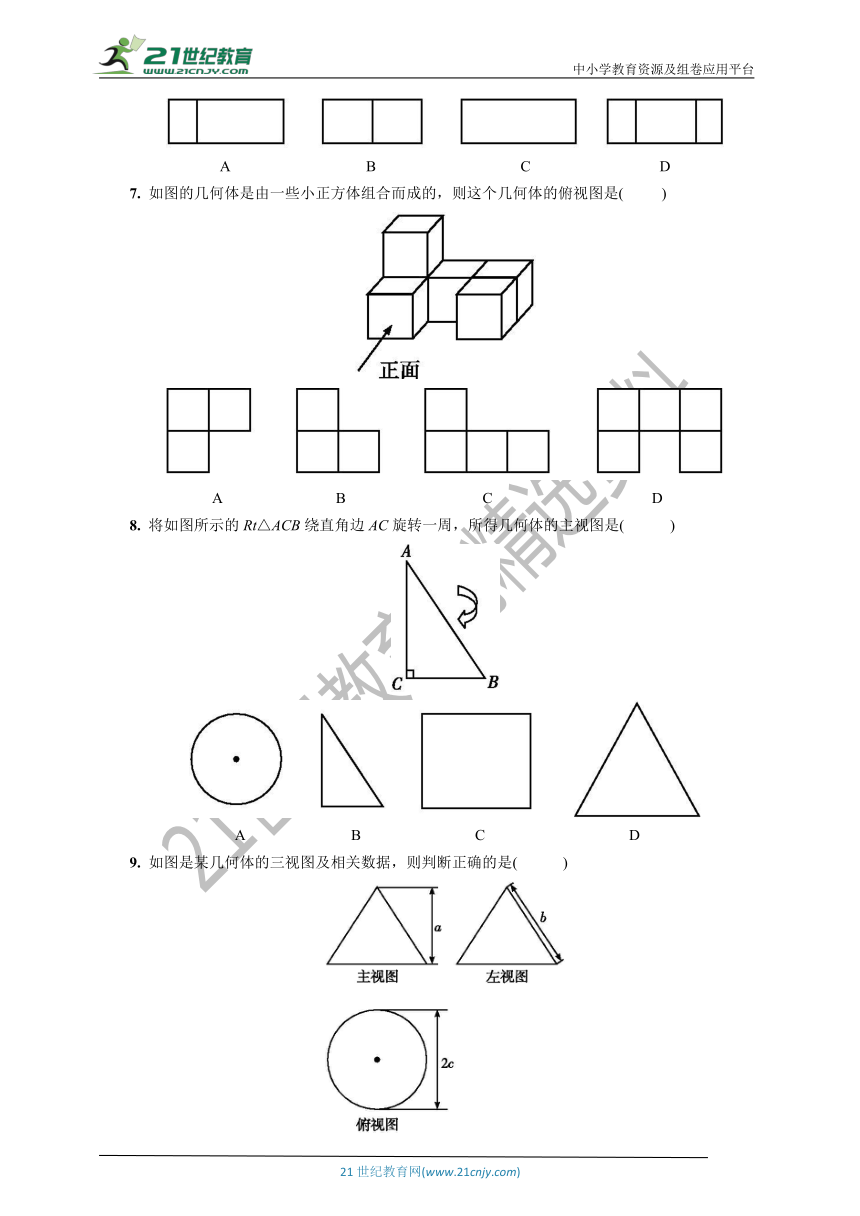
7.
如图的几何体是由一些小正方体组合而成的,则这个几何体的俯视图是(
)
A
B
C
D
8.
将如图所示的Rt△ACB绕直角边AC旋转一周,所得几何体的主视图是(
)
A
B
C
D
9.
如图是某几何体的三视图及相关数据,则判断正确的是(
)
A.
a2+b2=c2
B.
a2+b2=4c2
C.
a2+c2=b2
D.
a2+4c2=b2
10.
如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要
个小立方体,王亮所搭几何体的表面积为
.
11.
如图是一个工件的三视图,图中标有尺寸,则这个工件的体积是
.
12.
由几个相同的边长为1的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小立方块的个数.
(1)请在方格纸中分别画出这个几何体的主视图和左视图.
(2)根据三视图,请你求出这个组合几何体的表面积(包括底面积).
13.
如图,某几何体的主视图和左视图是由若干个大小相等的正方形构成的三视图.
(1)请描述这个几何体的形状;
(2)请根据图中所标的尺寸,计算这个几何体的表面积.
14.
如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
参
考
答
案
1.
C 【解析】该几何体的俯视图如图所示,则在所画的俯视图中正方形共有3个.故选C.
2.
①②③ 【解析】①圆锥主视图是三角形,左视图也是三角形;②圆柱的主视图和左视图都是矩形;③球的主视图和左视图都是圆形;④长方体的主视图是矩形,左视图也是矩形,但是长和宽不一定相同,故一定完全相同的几何体有①②③.
3.
解:如图所示.
(答案不唯一)
4.
B 【解析】该几何体的左视图如图所示,故选B.
5.
解:三视图如下
表面积S=(4×2+5×2+5×2)×(1×1)=28×1=28.
6.
B 【解析】从左边看去,应该是两个并列并且大小相同的矩形,故选B.
7.
D 【解析】从几何体的上面看共有3列小正方形,右边有2个,左边有2个,中间上面有1个,故选D.
8.
D 【解析】Rt△ACB绕直角边AC旋转一周,所得几何体是圆锥,主视图是等腰三角形.故选D.
9.
C 【解析】因为该几何体的主视图和左视图都是等腰三角形,俯视图是圆,所以该几何体为圆锥,且圆锥的底面半径为c,高为a,母线长为b.因为圆锥的底面半径,母线及圆锥的高构成直角三角形,所以a2+c2=b2.故选C.
10.
19 48 【解析】因为王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体,所以该长方体需要小立方体4×32=36个,因为张明用17个边长为1的小正方体搭成了一个几何体,所以王亮至少还需36-17=19个小立方体,表面积为:2×(9+7+8)=48,故答案为19,48.
11.
17π
cm3 【解析】由三视图可知,此工件为两个圆柱,大圆柱的底面直径是4
cm,高是4
cm,小圆柱的底面直径是2
cm,高是1
cm,所以工件的体积为V=π×22×4+π×12×1=17π(cm3).
12.
解:(1)图形如图所示.
(2)几何体的表面积为(3+4+5)×2×1×1=24.
13.
解:(1)因为主视图和左视图中都是正方形,所以该几何体中有2层柱体组成,因为俯视图中上面是圆,下面是4个正方形,所以该几何体是四个小正方体上面摆放一个圆柱体.
(2)因为16个边长为a的正方形的面积为16a2,圆柱的侧面积=πa×a=πa2,所以该几何体的表面积为16a2+πa2.
14.
解:(1)圆锥.
(2)S=S扇形+S圆=πrl+πr2=12π+4π=16π(平方厘米).
(3)如图将圆锥侧面展开,线段BD为所求的最短路程.由条件得,∠BAB′=120°,C为弧BB′中点,易得BD=3厘米.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
沪科版数学九年级下册同步课时训练
第25章
投影与视图
25.2 三视图
第1课时 三视图的定义及画法
要点测评
基础达标
要点1 三视图的概念、特征及画法
1.
由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有(
)
A.
1个
B.
2个
C.
3个
D.
4个
2.
如图,在常见的几何体圆锥,圆柱,球,长方体中,主视图与它的左视图一定完全相同的几何体有
(填编号).
3.
由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图.且使该主视图是轴对称图形.
要点2 三视图与立体图形的关系
4.
由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为(
)
A
B
C
D
5.
如图是七个棱长为1的立方块组成的一个几何体,画出其三视图并计算其表面积.
课后集训
巩固提升
6.
一个几何体及它的主视图和俯视图如图所示,那么它的左视图正确的是(
)
A
B
C
D
7.
如图的几何体是由一些小正方体组合而成的,则这个几何体的俯视图是(
)
A
B
C
D
8.
将如图所示的Rt△ACB绕直角边AC旋转一周,所得几何体的主视图是(
)
A
B
C
D
9.
如图是某几何体的三视图及相关数据,则判断正确的是(
)
A.
a2+b2=c2
B.
a2+b2=4c2
C.
a2+c2=b2
D.
a2+4c2=b2
10.
如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要
个小立方体,王亮所搭几何体的表面积为
.
11.
如图是一个工件的三视图,图中标有尺寸,则这个工件的体积是
.
12.
由几个相同的边长为1的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小立方块的个数.
(1)请在方格纸中分别画出这个几何体的主视图和左视图.
(2)根据三视图,请你求出这个组合几何体的表面积(包括底面积).
13.
如图,某几何体的主视图和左视图是由若干个大小相等的正方形构成的三视图.
(1)请描述这个几何体的形状;
(2)请根据图中所标的尺寸,计算这个几何体的表面积.
14.
如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
参
考
答
案
1.
C 【解析】该几何体的俯视图如图所示,则在所画的俯视图中正方形共有3个.故选C.
2.
①②③ 【解析】①圆锥主视图是三角形,左视图也是三角形;②圆柱的主视图和左视图都是矩形;③球的主视图和左视图都是圆形;④长方体的主视图是矩形,左视图也是矩形,但是长和宽不一定相同,故一定完全相同的几何体有①②③.
3.
解:如图所示.
(答案不唯一)
4.
B 【解析】该几何体的左视图如图所示,故选B.
5.
解:三视图如下
表面积S=(4×2+5×2+5×2)×(1×1)=28×1=28.
6.
B 【解析】从左边看去,应该是两个并列并且大小相同的矩形,故选B.
7.
D 【解析】从几何体的上面看共有3列小正方形,右边有2个,左边有2个,中间上面有1个,故选D.
8.
D 【解析】Rt△ACB绕直角边AC旋转一周,所得几何体是圆锥,主视图是等腰三角形.故选D.
9.
C 【解析】因为该几何体的主视图和左视图都是等腰三角形,俯视图是圆,所以该几何体为圆锥,且圆锥的底面半径为c,高为a,母线长为b.因为圆锥的底面半径,母线及圆锥的高构成直角三角形,所以a2+c2=b2.故选C.
10.
19 48 【解析】因为王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体,所以该长方体需要小立方体4×32=36个,因为张明用17个边长为1的小正方体搭成了一个几何体,所以王亮至少还需36-17=19个小立方体,表面积为:2×(9+7+8)=48,故答案为19,48.
11.
17π
cm3 【解析】由三视图可知,此工件为两个圆柱,大圆柱的底面直径是4
cm,高是4
cm,小圆柱的底面直径是2
cm,高是1
cm,所以工件的体积为V=π×22×4+π×12×1=17π(cm3).
12.
解:(1)图形如图所示.
(2)几何体的表面积为(3+4+5)×2×1×1=24.
13.
解:(1)因为主视图和左视图中都是正方形,所以该几何体中有2层柱体组成,因为俯视图中上面是圆,下面是4个正方形,所以该几何体是四个小正方体上面摆放一个圆柱体.
(2)因为16个边长为a的正方形的面积为16a2,圆柱的侧面积=πa×a=πa2,所以该几何体的表面积为16a2+πa2.
14.
解:(1)圆锥.
(2)S=S扇形+S圆=πrl+πr2=12π+4π=16π(平方厘米).
(3)如图将圆锥侧面展开,线段BD为所求的最短路程.由条件得,∠BAB′=120°,C为弧BB′中点,易得BD=3厘米.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
