沪科版八年级数学下册课件19.2.3平行四边形的判定(25张PPT)
文档属性
| 名称 | 沪科版八年级数学下册课件19.2.3平行四边形的判定(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-28 00:00:00 | ||
图片预览







文档简介
课件25张PPT。第十九章
四边形八年级数学沪科版·下册 19.2.3平行四边形的判定新课引入
平行四边形的性质边平行四边形的对边平行平行四边形的对边相等 角平行四边形的对角相等平行四边形的邻角互补 平行四边形的对角线互相平分 对称性平行四边形是中心对称图形 对角线新知探究
1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.2.平四边形的性质:性质3: 平行四边形的对角线互相平分.性质2: 平行四边形的对角相等.性质1: 平行四边形的对边相等. 平行四边形的定义有两层意思: (1) 若一个四边形
是平行四边形, 则它的两组对边就分别平行; (2)若一
个四边形的两组对边分别平行, 则它是平行四边形.新知探究
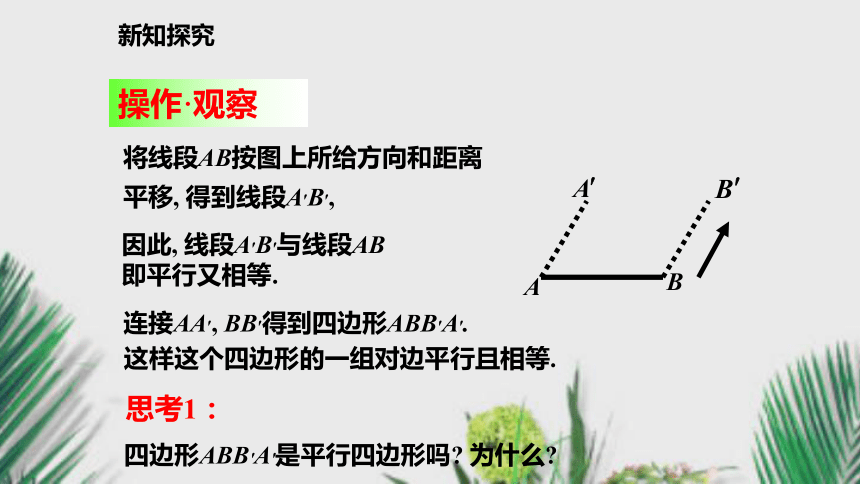
操作·观察AB将线段AB按图上所给方向和距离
平移, 得到线段A′B′, 连接AA′, BB′得到四边形ABB′A′.这样这个四边形的一组对边平行且相等.思考1:四边形ABB′A′是平行四边形吗? 为什么?因此, 线段A′B′与线段AB
即平行又相等.新知探究
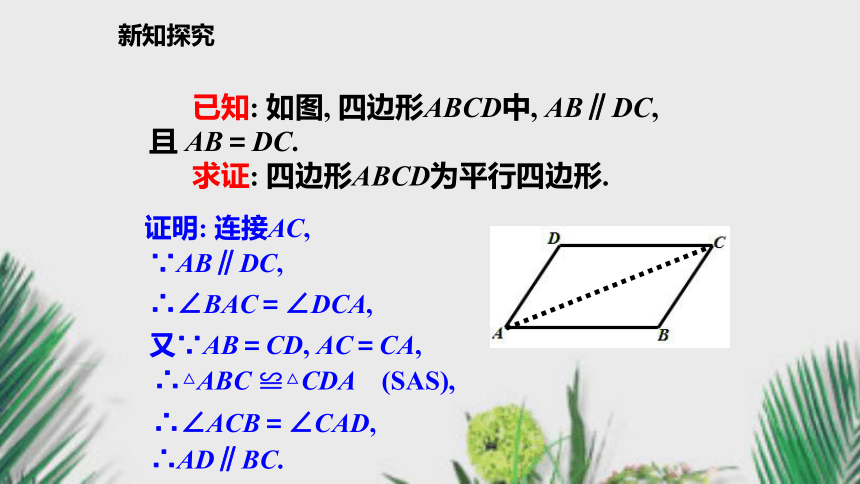
已知: 如图, 四边形ABCD中, AB∥DC,
且 AB=DC.
求证: 四边形ABCD为平行四边形.证明: 连接AC, ∵AB∥DC, ∴∠BAC=∠DCA, 又∵AB=CD, AC=CA, ∴△ABC ≌△CDA (SAS),∴∠ACB=∠CAD, ∴AD∥BC.新知探究 四边形ABCD是平行四边形. 由此可以看出, 四边形ABCD的两组对边就
分别平行, 因此根据平行四边形的定义可得出:新知探究一组对边平行且相等的四边形是平行四边形.∵AB=CD,AB∥CD∴四边形ABCD是平行四边形.几何语言:平行四边形判定定理1BDCA总结归纳新知探究例1 如图, 在平行四边形ABCD中, 已知AE, CF分别是∠DAB, ∠BCD的角平分线, 试证明四边形AFCE是平行四边形. 证明: ∵在平行四边形ABCD中,
AE, CF分别是∠DAB, ∠BCD的角平分线
∴∠B=∠D, AB=CD,
∠BAE=∠DCF= ∠DAB= ∠BCD. ∴△ABE≌△CDF (ASA),
∴BE=DF ∴AF=CE. ∵AF∥CE,
∴四边形AFCE是平行四边形. (一组对边平行且相等的四边形是平行四边形)新知探究思考1: 一组对边平行, 另一组对边相等的四边形是否一定是平行四边形? 新知探究5cm3cm4cm4cm3cm3cm3cm3cm发现: 一组对边平行, 另一组对边相等的四边形不一定是平行四边形.新知探究操作·思考如图, 过点A画两条线段AB, AD, 以点B圆心, AD长为半径画弧, 再以点D为圆心, AB长为半径画弧, 两弧
相交于C, 连接BC, DC, 这样得到两组对边分别相等
的四边形ABCD.ABDC·新知探究思考2: 这样做出来的四边形是平行四边形吗?
为什么?通过画图我们知道: AB=DC, AD=BC, 又∵AC=CA, ∴△ABC≌△CDA(SSS)∴∠CAB=∠DCA, ∴AB∥DC, ∵AB=DC, AB∥DC∴四边形ABCD是平行四边形.新知探究两组对边分别相等的四边形是平行四边形.∵AB=CD, AD=BC,∴四边形ABCD是平行四边形.几何语言:平行四边形判定定理2BDCA总结归纳新知探究操作·思考如图, 作两条直线l1, l2相交于点O, OABCD在直线l1上截取OA=OC,
在直线l2上截取OB=OD, 连接AB, BC, CD, DA, 这样画出来的四边形ABCD
的对角线就互相平分.l1l2新知探究这个四边形是平行四边形吗?思考3:由作图可知: OA=OC, OB=OD, 又∵∠AOD=∠BOC (对顶角相等) ,∴△AOD≌△BOC (SAS)∴∠DAO=∠BCO, ∴AD∥BC, 同理可得: AB∥DC, ∴四边形ABCD是平行四边形.新知探究对角线互相平分的四边形是平行四边形.∵AO=CO,BO=DO∴四边形ABCD是平行四边形.几何语言:平行四边形判定定理3总结归纳新知探究思考4: 我们可以从角出发来判定一个四边形是否为平行四边形吗? 你能根据平行四边形的定义证明它们吗?新知探究已知: 四边形ABCD中, ∠A=∠C, ∠B=∠D,
求证: 四边形ABCD是平行四边形.又∵∠A=∠C, ∠B=∠D,∵∠A+∠C+∠B+∠D=360°,∴2∠A+2∠B=360°.即∠A+∠B=180°.∴ AD∥BC,∴四边形ABCD是平行四边形.同理得 AB∥ CD,证明: 定义判定:
两组对角分别相等的四边形是平行四边形新知探究 1.已知: 如图, 点E, F是 ABCD的对角线AC上两
点, 且AE=CF, 求证: 四边形BEDF是平行四边形.证明: 连接BD交AC于点O, ∵四边形ABCD是平行四边形, ∴AO=CO, BO=DO, ∵AE=CF, ∴OE=AO-AE=CO-CF=OF, ∴四边形BEDF是平行四边形.O新知探究 2.如图, 四边形ABCD是平行四边形, E, F
是对角线BD上的点, ∠1=∠2. 求证: AF∥CE.证明: ∵四边形ABCD
是平行四边形, ∴AB=CD, AB∥CD, ∴∠3=∠4, ∵∠1=∠2, ∴∠AEB=∠DFC, 新知探究在△ABE 和△CDF 中,∴ △ABE≌△CDF(AAS)∴ AE=CF, 又∵∠1=∠2, ∴AE∥CF, ∴四边形AECF是平行四边形,∴AF∥CE.课堂小结从边考虑两组对边分别平行的四边形是平行四边形 (定义法)两组对边分别相等的四边形是平行四边形 (判定定理1)一组对边平行且相等的四边形是平行四边形 (判定定理2)从角考虑从对角线考虑平行四边形的判定方法两组对角分别相等的四边形是平行四边形 (定义拓展)对角线互相平分的四边形是平行四边形 (判定定理3)课堂小测1.已知: 如图, 在四边形ABCD中, ∠A=∠C,
∠B=∠D. 试判断四边形ABCD是否是平行四
边形, 并说明理由.∵∠A=∠C, ∠B=∠D, 而∠A+∠B+∠C+∠D=360°, ∴2∠A+2∠B=360°, ∴∠A+∠B=180°, ∴AD//BC, 同理可证: AB//CD ∴四边形ABCD是平行四边形 .课堂小测2.画□ABCD, 使AB=2cm, BC=3cm,
AC=4cm.ABCD用直尺画2cm的线段AB, 用圆规以A为圆心, 4cm为半径画弧, 再以B为圆心3cm为半径画弧, 两弧交点为C, 连接AC, BC, 过C做CD=2cm, 且平行于AB, 连接AD, 即可得□ABCD.课堂小测 3.如图, E, F是四边形ABCD的对角线AC上
两点, AF=CE, DF=BE, DF∥BE,
求证: 四边形ABCD是平行四边形.证明: ∵DF∥BE, ∴∠DFE=∠BEF, ∴∠AFD=∠CEB, 又∵AF=CE, DF=BE, ∴△AFD≌△CEB(SAS),∴∠DAC=∠BCA, AD=BC, ∴AD∥BC,∴四边形ABCD是平行四边形.
平行四边形的性质边平行四边形的对边平行平行四边形的对边相等 角平行四边形的对角相等平行四边形的邻角互补 平行四边形的对角线互相平分 对称性平行四边形是中心对称图形 对角线新知探究
1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.2.平四边形的性质:性质3: 平行四边形的对角线互相平分.性质2: 平行四边形的对角相等.性质1: 平行四边形的对边相等. 平行四边形的定义有两层意思: (1) 若一个四边形
是平行四边形, 则它的两组对边就分别平行; (2)若一
个四边形的两组对边分别平行, 则它是平行四边形.新知探究
操作·观察AB将线段AB按图上所给方向和距离
平移, 得到线段A′B′, 连接AA′, BB′得到四边形ABB′A′.这样这个四边形的一组对边平行且相等.思考1:四边形ABB′A′是平行四边形吗? 为什么?因此, 线段A′B′与线段AB
即平行又相等.新知探究
已知: 如图, 四边形ABCD中, AB∥DC,
且 AB=DC.
求证: 四边形ABCD为平行四边形.证明: 连接AC, ∵AB∥DC, ∴∠BAC=∠DCA, 又∵AB=CD, AC=CA, ∴△ABC ≌△CDA (SAS),∴∠ACB=∠CAD, ∴AD∥BC.新知探究 四边形ABCD是平行四边形. 由此可以看出, 四边形ABCD的两组对边就
分别平行, 因此根据平行四边形的定义可得出:新知探究一组对边平行且相等的四边形是平行四边形.∵AB=CD,AB∥CD∴四边形ABCD是平行四边形.几何语言:平行四边形判定定理1BDCA总结归纳新知探究例1 如图, 在平行四边形ABCD中, 已知AE, CF分别是∠DAB, ∠BCD的角平分线, 试证明四边形AFCE是平行四边形. 证明: ∵在平行四边形ABCD中,
AE, CF分别是∠DAB, ∠BCD的角平分线
∴∠B=∠D, AB=CD,
∠BAE=∠DCF= ∠DAB= ∠BCD. ∴△ABE≌△CDF (ASA),
∴BE=DF ∴AF=CE. ∵AF∥CE,
∴四边形AFCE是平行四边形. (一组对边平行且相等的四边形是平行四边形)新知探究思考1: 一组对边平行, 另一组对边相等的四边形是否一定是平行四边形? 新知探究5cm3cm4cm4cm3cm3cm3cm3cm发现: 一组对边平行, 另一组对边相等的四边形不一定是平行四边形.新知探究操作·思考如图, 过点A画两条线段AB, AD, 以点B圆心, AD长为半径画弧, 再以点D为圆心, AB长为半径画弧, 两弧
相交于C, 连接BC, DC, 这样得到两组对边分别相等
的四边形ABCD.ABDC·新知探究思考2: 这样做出来的四边形是平行四边形吗?
为什么?通过画图我们知道: AB=DC, AD=BC, 又∵AC=CA, ∴△ABC≌△CDA(SSS)∴∠CAB=∠DCA, ∴AB∥DC, ∵AB=DC, AB∥DC∴四边形ABCD是平行四边形.新知探究两组对边分别相等的四边形是平行四边形.∵AB=CD, AD=BC,∴四边形ABCD是平行四边形.几何语言:平行四边形判定定理2BDCA总结归纳新知探究操作·思考如图, 作两条直线l1, l2相交于点O, OABCD在直线l1上截取OA=OC,
在直线l2上截取OB=OD, 连接AB, BC, CD, DA, 这样画出来的四边形ABCD
的对角线就互相平分.l1l2新知探究这个四边形是平行四边形吗?思考3:由作图可知: OA=OC, OB=OD, 又∵∠AOD=∠BOC (对顶角相等) ,∴△AOD≌△BOC (SAS)∴∠DAO=∠BCO, ∴AD∥BC, 同理可得: AB∥DC, ∴四边形ABCD是平行四边形.新知探究对角线互相平分的四边形是平行四边形.∵AO=CO,BO=DO∴四边形ABCD是平行四边形.几何语言:平行四边形判定定理3总结归纳新知探究思考4: 我们可以从角出发来判定一个四边形是否为平行四边形吗? 你能根据平行四边形的定义证明它们吗?新知探究已知: 四边形ABCD中, ∠A=∠C, ∠B=∠D,
求证: 四边形ABCD是平行四边形.又∵∠A=∠C, ∠B=∠D,∵∠A+∠C+∠B+∠D=360°,∴2∠A+2∠B=360°.即∠A+∠B=180°.∴ AD∥BC,∴四边形ABCD是平行四边形.同理得 AB∥ CD,证明: 定义判定:
两组对角分别相等的四边形是平行四边形新知探究 1.已知: 如图, 点E, F是 ABCD的对角线AC上两
点, 且AE=CF, 求证: 四边形BEDF是平行四边形.证明: 连接BD交AC于点O, ∵四边形ABCD是平行四边形, ∴AO=CO, BO=DO, ∵AE=CF, ∴OE=AO-AE=CO-CF=OF, ∴四边形BEDF是平行四边形.O新知探究 2.如图, 四边形ABCD是平行四边形, E, F
是对角线BD上的点, ∠1=∠2. 求证: AF∥CE.证明: ∵四边形ABCD
是平行四边形, ∴AB=CD, AB∥CD, ∴∠3=∠4, ∵∠1=∠2, ∴∠AEB=∠DFC, 新知探究在△ABE 和△CDF 中,∴ △ABE≌△CDF(AAS)∴ AE=CF, 又∵∠1=∠2, ∴AE∥CF, ∴四边形AECF是平行四边形,∴AF∥CE.课堂小结从边考虑两组对边分别平行的四边形是平行四边形 (定义法)两组对边分别相等的四边形是平行四边形 (判定定理1)一组对边平行且相等的四边形是平行四边形 (判定定理2)从角考虑从对角线考虑平行四边形的判定方法两组对角分别相等的四边形是平行四边形 (定义拓展)对角线互相平分的四边形是平行四边形 (判定定理3)课堂小测1.已知: 如图, 在四边形ABCD中, ∠A=∠C,
∠B=∠D. 试判断四边形ABCD是否是平行四
边形, 并说明理由.∵∠A=∠C, ∠B=∠D, 而∠A+∠B+∠C+∠D=360°, ∴2∠A+2∠B=360°, ∴∠A+∠B=180°, ∴AD//BC, 同理可证: AB//CD ∴四边形ABCD是平行四边形 .课堂小测2.画□ABCD, 使AB=2cm, BC=3cm,
AC=4cm.ABCD用直尺画2cm的线段AB, 用圆规以A为圆心, 4cm为半径画弧, 再以B为圆心3cm为半径画弧, 两弧交点为C, 连接AC, BC, 过C做CD=2cm, 且平行于AB, 连接AD, 即可得□ABCD.课堂小测 3.如图, E, F是四边形ABCD的对角线AC上
两点, AF=CE, DF=BE, DF∥BE,
求证: 四边形ABCD是平行四边形.证明: ∵DF∥BE, ∴∠DFE=∠BEF, ∴∠AFD=∠CEB, 又∵AF=CE, DF=BE, ∴△AFD≌△CEB(SAS),∴∠DAC=∠BCA, AD=BC, ∴AD∥BC,∴四边形ABCD是平行四边形.
