沪科版八年级数学下册:19.2.1平行四边形的边和角的性质 课件(共22张PPT)
文档属性
| 名称 | 沪科版八年级数学下册:19.2.1平行四边形的边和角的性质 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-28 00:00:00 | ||
图片预览



文档简介
课件22张PPT。第十九章
四边形八年级数学沪科版·下册19.2.1平行四边形的边和角的性质新课引入
观察下图, 平行四边形在生活中无处不在.新知探究
你还能举出其他的例子吗?新知探究
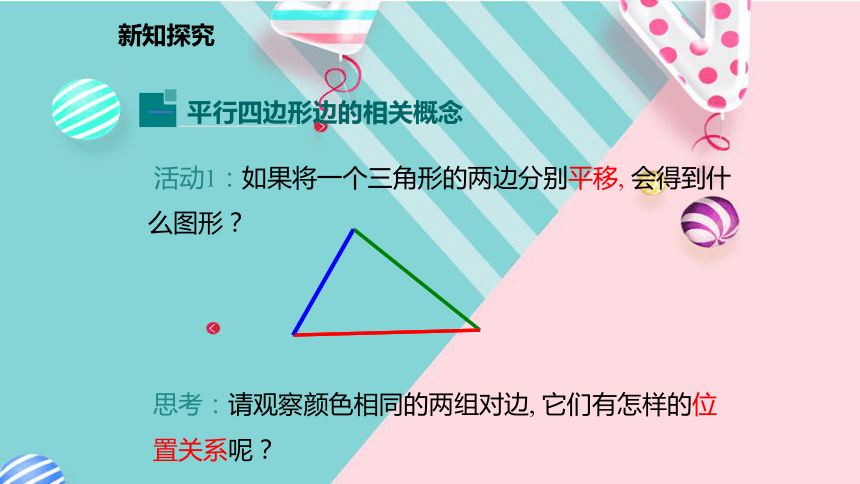
活动1:如果将一个三角形的两边分别平移, 会得到什么图形?思考:请观察颜色相同的两组对边, 它们有怎样的位置关系呢?新知探究
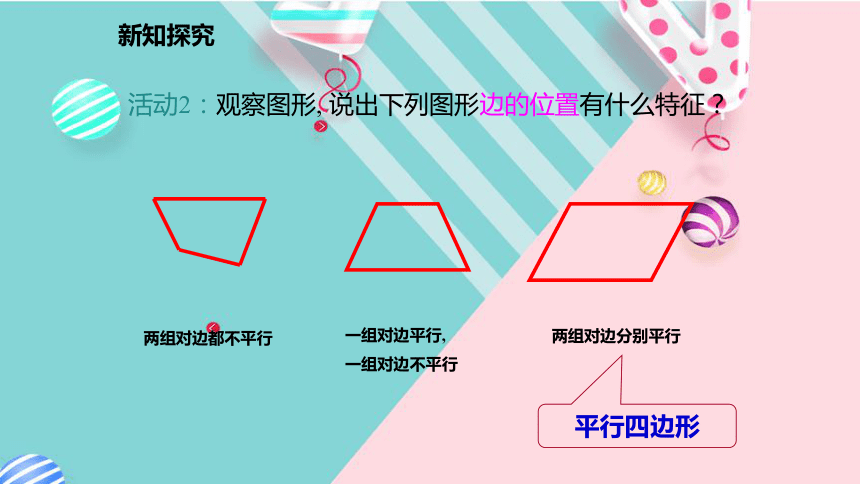
两组对边都不平行一组对边平行,
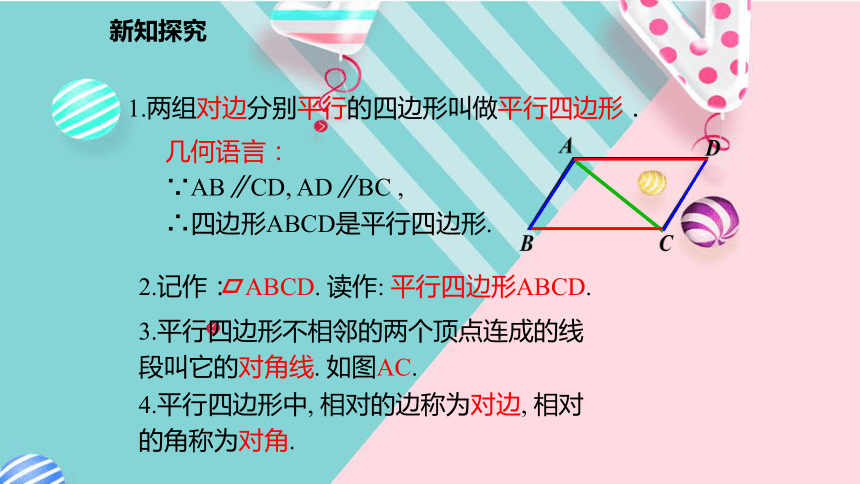
一组对边不平行两组对边分别平行平行四边形活动2:观察图形, 说出下列图形边的位置有什么特征?新知探究1.两组对边分别平行的四边形叫做平行四边形. 几何语言:
∵AB∥CD, AD∥BC ,
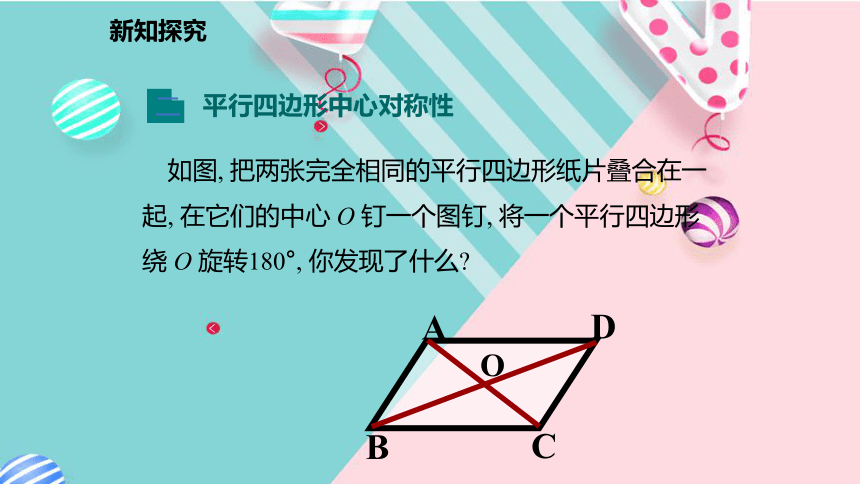
∴四边形ABCD是平行四边形.3.平行四边形不相邻的两个顶点连成的线段叫它的对角线. 如图AC.4.平行四边形中, 相对的边称为对边, 相对的角称为对角.新知探究 如图, 把两张完全相同的平行四边形纸片叠合在一起, 在它们的中心 O 钉一个图钉, 将一个平行四边形绕 O 旋转180°, 你发现了什么? 平行四边形中心对称性一二新知探究再看一遍新知探究你有什么猜想?新知探究根据刚才的旋转, 你知道平行四边形是什么图形?猜一猜 □ABCD绕它的中心O旋转180°后与自身重合, 这时我们说□ABCD是中心对称图形, 两条对角线的交点O是它的对称中心. 平行四边形是中心对称图形, 两条对角线的交点是它的对称中心. 新知探究 平行四边形的一条对角线把平行四边形分成两个全等的三角形;ABCD四边形问题转化三角形问题方法:推理证明新知探究证明: 如图, 连接AC
∵AD∥BC, AB ∥ CD
∴∠1=∠2, ∠3=∠4
又AC是△ABC 和△CDA 的公共边
∴ △ABC ≌ △CDA(ASA)
∴ AB=CD, BC=DA, ∠B=∠D又∵∠1=∠2, ∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.新知探究思考: 不添加辅助线, 你能否直接运用平行四边形
的定义, 证明其对角相等?ABCD证明: ∵AB∥ DC
∠ABC+∠BCD=180°
AD∥ BC
∴∠BAD+∠ABC=180°
∴∠BCD=∠BAD
同理 ∠ABC=∠ADC新知探究几 何 语 言边角文字叙述对边平行对边相等对角相等∵ 四边形ABCD是平行四边形, ∴ AD∥BC, AB∥DC.∴ AD=BC, AB=DC.∵ 四边形ABCD是平行四边形, ∴ ∠ A=∠C, ∠ B=∠D.∵ 四边形ABCD是平行四边形, 平行四边形的性质性质定理1性质定理2新知探究例1 已知: ABCD, E, F是对角线AC上的两点, 并且AE=CF, 求证: BE=DF. 证明: ∵四边形ABCD是平行四边形, ∴∠BAE=∠DCF.∴ △ABE≌△CDF(SAS).∴ AB=CD, AB ∥ CD又∵AE=CF, ∴ BE=DF.新知探究例2 有一块形状如图所示的玻璃, 不小心把EDF部分打碎了, 现在只测得AE=60cm, BC=80cm, ∠B=60°且AE∥ BC, AB∥ CF, 你能根据测得的数据计算出DE的长度和∠D的度数吗?解∵AE//BC, AB//CF∴四边形ABCD是平行四边形∴∠D=∠B=60°,
AD=BC=60cm.∴ED=AD-AE=80-60=20cm.答:DE的长度是20cm, ∠D的度数是60°.新知探究A1A3A2练一练: 学校买了四棵树, 准备栽在花园里, 已经栽了三棵(如图), 现在学校希望这四棵树能组成一个平行四边形, 你觉得第四棵树应该栽在哪里?课堂小结平行四边形中心对称图形, 两条对角线的交点是它的对称中心两组对边分别平行的四边形是平行四边形对称性定义性质对边平行, 对边相等, 对角相等课堂小测1 .如图, 在 ABCD中 (1)若∠A=130°, 则∠B=______ , ∠C=______ ,
∠D=______. (2)若∠A+∠C= 200°, 则∠A=______ , ∠B=______. (3)若∠A:∠B= 5:4, 则∠C=______ , ∠D=______.
(4)若AB=3, BC=5, 则它的周长= ______.50°130°50°100°80°100°80°16课堂小测2.在 □ ABCD中, ∠A=150°, AB=8cm, BC=10cm,
则S□ABCD = .提示:过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.40cm2课堂小测解: 在平行四边形ABCD中, AB=DC,
AD=BC(平行四边形的对边相等)
∵ AB=8, DC=8
又∵AB+BC+DC+AD=24,
∴AD=BC= (24-2AB)=4.3.如图, 在 ABCD中, AB=8, 周长等于24, 求其余三条边的长.BCDA课堂小测4.已知点 A(3, 0), B(-1, 0), C(0, 2), 以 A, B, C为顶点画平行四边形, 你能求出第四个顶点 D 吗?(4, 2)(2, -2)(-4, 2)
观察下图, 平行四边形在生活中无处不在.新知探究
你还能举出其他的例子吗?新知探究
活动1:如果将一个三角形的两边分别平移, 会得到什么图形?思考:请观察颜色相同的两组对边, 它们有怎样的位置关系呢?新知探究
两组对边都不平行一组对边平行,
一组对边不平行两组对边分别平行平行四边形活动2:观察图形, 说出下列图形边的位置有什么特征?新知探究1.两组对边分别平行的四边形叫做平行四边形. 几何语言:
∵AB∥CD, AD∥BC ,
∴四边形ABCD是平行四边形.3.平行四边形不相邻的两个顶点连成的线段叫它的对角线. 如图AC.4.平行四边形中, 相对的边称为对边, 相对的角称为对角.新知探究 如图, 把两张完全相同的平行四边形纸片叠合在一起, 在它们的中心 O 钉一个图钉, 将一个平行四边形绕 O 旋转180°, 你发现了什么? 平行四边形中心对称性一二新知探究再看一遍新知探究你有什么猜想?新知探究根据刚才的旋转, 你知道平行四边形是什么图形?猜一猜 □ABCD绕它的中心O旋转180°后与自身重合, 这时我们说□ABCD是中心对称图形, 两条对角线的交点O是它的对称中心. 平行四边形是中心对称图形, 两条对角线的交点是它的对称中心. 新知探究 平行四边形的一条对角线把平行四边形分成两个全等的三角形;ABCD四边形问题转化三角形问题方法:推理证明新知探究证明: 如图, 连接AC
∵AD∥BC, AB ∥ CD
∴∠1=∠2, ∠3=∠4
又AC是△ABC 和△CDA 的公共边
∴ △ABC ≌ △CDA(ASA)
∴ AB=CD, BC=DA, ∠B=∠D又∵∠1=∠2, ∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.新知探究思考: 不添加辅助线, 你能否直接运用平行四边形
的定义, 证明其对角相等?ABCD证明: ∵AB∥ DC
∠ABC+∠BCD=180°
AD∥ BC
∴∠BAD+∠ABC=180°
∴∠BCD=∠BAD
同理 ∠ABC=∠ADC新知探究几 何 语 言边角文字叙述对边平行对边相等对角相等∵ 四边形ABCD是平行四边形, ∴ AD∥BC, AB∥DC.∴ AD=BC, AB=DC.∵ 四边形ABCD是平行四边形, ∴ ∠ A=∠C, ∠ B=∠D.∵ 四边形ABCD是平行四边形, 平行四边形的性质性质定理1性质定理2新知探究例1 已知: ABCD, E, F是对角线AC上的两点, 并且AE=CF, 求证: BE=DF. 证明: ∵四边形ABCD是平行四边形, ∴∠BAE=∠DCF.∴ △ABE≌△CDF(SAS).∴ AB=CD, AB ∥ CD又∵AE=CF, ∴ BE=DF.新知探究例2 有一块形状如图所示的玻璃, 不小心把EDF部分打碎了, 现在只测得AE=60cm, BC=80cm, ∠B=60°且AE∥ BC, AB∥ CF, 你能根据测得的数据计算出DE的长度和∠D的度数吗?解∵AE//BC, AB//CF∴四边形ABCD是平行四边形∴∠D=∠B=60°,
AD=BC=60cm.∴ED=AD-AE=80-60=20cm.答:DE的长度是20cm, ∠D的度数是60°.新知探究A1A3A2练一练: 学校买了四棵树, 准备栽在花园里, 已经栽了三棵(如图), 现在学校希望这四棵树能组成一个平行四边形, 你觉得第四棵树应该栽在哪里?课堂小结平行四边形中心对称图形, 两条对角线的交点是它的对称中心两组对边分别平行的四边形是平行四边形对称性定义性质对边平行, 对边相等, 对角相等课堂小测1 .如图, 在 ABCD中 (1)若∠A=130°, 则∠B=______ , ∠C=______ ,
∠D=______. (2)若∠A+∠C= 200°, 则∠A=______ , ∠B=______. (3)若∠A:∠B= 5:4, 则∠C=______ , ∠D=______.
(4)若AB=3, BC=5, 则它的周长= ______.50°130°50°100°80°100°80°16课堂小测2.在 □ ABCD中, ∠A=150°, AB=8cm, BC=10cm,
则S□ABCD = .提示:过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.40cm2课堂小测解: 在平行四边形ABCD中, AB=DC,
AD=BC(平行四边形的对边相等)
∵ AB=8, DC=8
又∵AB+BC+DC+AD=24,
∴AD=BC= (24-2AB)=4.3.如图, 在 ABCD中, AB=8, 周长等于24, 求其余三条边的长.BCDA课堂小测4.已知点 A(3, 0), B(-1, 0), C(0, 2), 以 A, B, C为顶点画平行四边形, 你能求出第四个顶点 D 吗?(4, 2)(2, -2)(-4, 2)
