人教版数学七年级下册:5.1.1相交线 课件(共31张PPT)
文档属性
| 名称 | 人教版数学七年级下册:5.1.1相交线 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-28 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
导入
生活中的相交直线
生活中的相交直线
生活中的相交直线
知识与能力
1.理解对顶角与邻补角的概念,能从图中辨认对顶角与邻补角;
2.掌握对顶角的性质 ;
4.理解对顶角相等的说理过程.
教学目标
过程与方法
1.经历探究对顶角、邻补角的位置关系的过程,建立空间观念;
2.通过分析具体图形得到对顶角、邻补角的概念,发展自己的概括能力.
教学目标
情感态度与价值观
1.通过对顶角的探究,初步认识数学与现实生活的密切联系;
2.通过交流活动,在学习活动中培养良好的情感、合作交流、主动参与的意识.
教学目标
重点
对顶角的概念,对顶角性质与应用.
难点
理解对顶角相等的性质的探索.
教学重难点
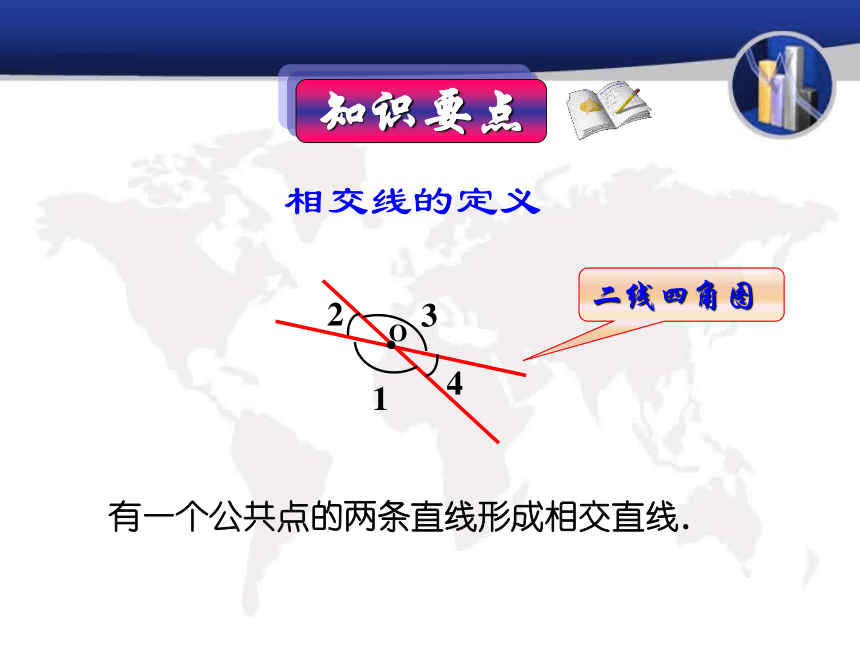
有一个公共点的两条直线形成相交直线.
相交线的定义
●
O
1
2
3
4
知识要点
二线四角图
请你画出任意两条相交直线,看看这四个角有什么关系?
两条相交直线形成的小于平角的角有几个?
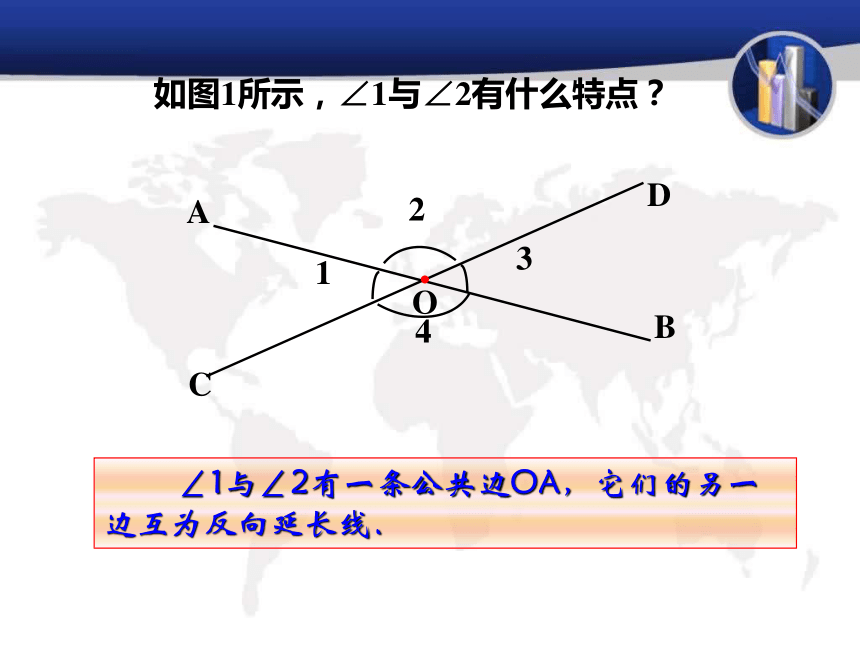
如图1所示,∠1与∠2有什么特点?
∠1与∠2有一条公共边OA,它们的另一边互为反向延长线.
2
3
1
4
A
B
C
D
O
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
图中互为邻补角的有:∠1与∠2, ∠2与∠3,
∠3与∠4, ∠1与∠4.
知识要点
邻补角
O
C
D
A
B
1
3
4
2
判断两个角是不是邻补角:
(1)有一个公共顶点;
(2)有一条公共边.
归纳
一对邻补角一定互补吗?
一对互补的角一定是邻补角吗?
图中,∠1和∠2、∠2和∠3、∠3和∠4,∠1和∠4都是邻补角,它们是相互的、成对出现的,如∠2是∠3的邻补角,∠1是∠4的邻补角,单独的一个∠1或单独的一个∠4都不能叫邻补角.
O
C
D
A
B
1
3
4
2
C
A
1
O
O
C
B
4
?
下列图中∠1、∠2还是邻补角吗?
1
2
1
2
1
2
如图1所示,∠1与∠3有什么特点?
∠1与∠3是直线AB与CD相交得到的,它们有一个公共顶点O,没有公共边.
2
3
1
4
A
B
C
D
O
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
右图中互为对顶角的为:
∠1与∠3; ∠2与∠4.
知识要点
对顶角
O
C
D
A
B
1
3
4
2
判断两个角是不是对顶角:
(1)两个角是由两条直线相交而形成的(由两条直线相交保证了所形成的角有公共顶点);
(2)两个角的两边无公共边.
归纳
下列各图中∠1、∠2是对顶角吗?为什么?
2
1
1
2
1
2
对顶角是成对出现的.上图中,∠2和∠4它们是相互的,∠2是∠4的对顶角, ∠4是∠2的对顶角,而单独的一个∠2或一个单独的∠4都不能叫对顶角.
O
C
D
A
B
1
3
4
2
O
A
2
D
O
C
B
4
两条直线相交,有____组对顶角.
三条直线相交于一点,有____组对顶角.
2
6
四条直线相交于一点,有____组对顶角.
n条直线相交于一点,有_________组对顶角.
12
n(n-1)
∠1与∠2互补, ∠2 与∠3互补
∠1= ∠3
(同角的补角相等)
∠2=∠4
对顶角相等.
O
C
D
A
B
1
3
4
2
知识要点
对顶角性质
对顶角相等.
例:如图所示,直线m,n相交,∠1=60°,求∠2,∠3,∠4的度数.
m
n
1
2
3
4
解:由邻补角的定义,可得:
∠2=180°-∠1
=180°-60°
=120°;
由对顶相等,可得:
∠3=∠1=60°,
∠4=∠2=120°.
角的
名称 特 征 性 质 相 同 点 不 同 点
对
顶
角
邻
补
角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对邻补角有四对
①有无公共边
课堂小结
(1)有公共顶点且相等的两个角是对顶角.( )
(2)两条直线相交,有两组对顶角.( )
1.判断
×
√
随堂练习
2.如右图直线AB、CD交于点O,OP为射线,那么( )
A.∠AOC和∠BOC是对顶角
B.∠BOC和∠AOP是对顶角
C.∠BOC和∠AOD是对顶角
D.∠AOC和∠DOP是对顶角
C
D
A
B
O
P
C
3.如图,直线a,b相交于点O,若∠1=40°,则∠2=( )
A.60° B.100° C.120° D.140°
1
2
O
a
b
D
C
D
A
B
O
P
2.直线AB、CD交于点O,OP是∠BOC的平分线,已知∠AOC=54°.求∠BOP的度数.
解: 由邻补角的定义可得:
∠BOC=180°-∠AOC
=180°-54°
=126°;
因为OP平分∠BOC,
所以∠BOP= ∠AOD
= ×126°
=63°.
导入
生活中的相交直线
生活中的相交直线
生活中的相交直线
知识与能力
1.理解对顶角与邻补角的概念,能从图中辨认对顶角与邻补角;
2.掌握对顶角的性质 ;
4.理解对顶角相等的说理过程.
教学目标
过程与方法
1.经历探究对顶角、邻补角的位置关系的过程,建立空间观念;
2.通过分析具体图形得到对顶角、邻补角的概念,发展自己的概括能力.
教学目标
情感态度与价值观
1.通过对顶角的探究,初步认识数学与现实生活的密切联系;
2.通过交流活动,在学习活动中培养良好的情感、合作交流、主动参与的意识.
教学目标
重点
对顶角的概念,对顶角性质与应用.
难点
理解对顶角相等的性质的探索.
教学重难点
有一个公共点的两条直线形成相交直线.
相交线的定义
●
O
1
2
3
4
知识要点
二线四角图
请你画出任意两条相交直线,看看这四个角有什么关系?
两条相交直线形成的小于平角的角有几个?
如图1所示,∠1与∠2有什么特点?
∠1与∠2有一条公共边OA,它们的另一边互为反向延长线.
2
3
1
4
A
B
C
D
O
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
图中互为邻补角的有:∠1与∠2, ∠2与∠3,
∠3与∠4, ∠1与∠4.
知识要点
邻补角
O
C
D
A
B
1
3
4
2
判断两个角是不是邻补角:
(1)有一个公共顶点;
(2)有一条公共边.
归纳
一对邻补角一定互补吗?
一对互补的角一定是邻补角吗?
图中,∠1和∠2、∠2和∠3、∠3和∠4,∠1和∠4都是邻补角,它们是相互的、成对出现的,如∠2是∠3的邻补角,∠1是∠4的邻补角,单独的一个∠1或单独的一个∠4都不能叫邻补角.
O
C
D
A
B
1
3
4
2
C
A
1
O
O
C
B
4
?
下列图中∠1、∠2还是邻补角吗?
1
2
1
2
1
2
如图1所示,∠1与∠3有什么特点?
∠1与∠3是直线AB与CD相交得到的,它们有一个公共顶点O,没有公共边.
2
3
1
4
A
B
C
D
O
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
右图中互为对顶角的为:
∠1与∠3; ∠2与∠4.
知识要点
对顶角
O
C
D
A
B
1
3
4
2
判断两个角是不是对顶角:
(1)两个角是由两条直线相交而形成的(由两条直线相交保证了所形成的角有公共顶点);
(2)两个角的两边无公共边.
归纳
下列各图中∠1、∠2是对顶角吗?为什么?
2
1
1
2
1
2
对顶角是成对出现的.上图中,∠2和∠4它们是相互的,∠2是∠4的对顶角, ∠4是∠2的对顶角,而单独的一个∠2或一个单独的∠4都不能叫对顶角.
O
C
D
A
B
1
3
4
2
O
A
2
D
O
C
B
4
两条直线相交,有____组对顶角.
三条直线相交于一点,有____组对顶角.
2
6
四条直线相交于一点,有____组对顶角.
n条直线相交于一点,有_________组对顶角.
12
n(n-1)
∠1与∠2互补, ∠2 与∠3互补
∠1= ∠3
(同角的补角相等)
∠2=∠4
对顶角相等.
O
C
D
A
B
1
3
4
2
知识要点
对顶角性质
对顶角相等.
例:如图所示,直线m,n相交,∠1=60°,求∠2,∠3,∠4的度数.
m
n
1
2
3
4
解:由邻补角的定义,可得:
∠2=180°-∠1
=180°-60°
=120°;
由对顶相等,可得:
∠3=∠1=60°,
∠4=∠2=120°.
角的
名称 特 征 性 质 相 同 点 不 同 点
对
顶
角
邻
补
角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对邻补角有四对
①有无公共边
课堂小结
(1)有公共顶点且相等的两个角是对顶角.( )
(2)两条直线相交,有两组对顶角.( )
1.判断
×
√
随堂练习
2.如右图直线AB、CD交于点O,OP为射线,那么( )
A.∠AOC和∠BOC是对顶角
B.∠BOC和∠AOP是对顶角
C.∠BOC和∠AOD是对顶角
D.∠AOC和∠DOP是对顶角
C
D
A
B
O
P
C
3.如图,直线a,b相交于点O,若∠1=40°,则∠2=( )
A.60° B.100° C.120° D.140°
1
2
O
a
b
D
C
D
A
B
O
P
2.直线AB、CD交于点O,OP是∠BOC的平分线,已知∠AOC=54°.求∠BOP的度数.
解: 由邻补角的定义可得:
∠BOC=180°-∠AOC
=180°-54°
=126°;
因为OP平分∠BOC,
所以∠BOP= ∠AOD
= ×126°
=63°.
