五年级下册数学一课一练-3.5问题解决 西师大版 (含解析)
文档属性
| 名称 | 五年级下册数学一课一练-3.5问题解决 西师大版 (含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 50.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-28 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-3.5问题解决
一、单选题
1.一个长方体的汽油桶,底面积是15平方分米,高是6分米,如果1升汽油重0.74千克,这个油桶可以装汽油(?? )
A.?66.6千克????????????????????????????B.?63.6千克????????????????????????????C.?6.6千克????????????????????????????D.?6.66千克
2.长方体的6个面(?? )。
A.?一定都是长方形?????????????????B.?一定都是正方形?????????????????C.?可能有长方形也可能有正方形
3.正方体的棱长缩小3倍,它的体积缩小(?? )倍。
A.?3?????????????????????????????????????????????B.?9?????????????????????????????????????????????C.?27
4.一个长方体正好可以切成两个棱长是3厘米的正方体,这个长方体的表面积是(?? )。?
A.?108平方厘米?????????????????????????????B.?54平方厘米?????????????????????????????C.?90平方厘米
二、判断题
5.判断棱长之和相等的两个正方体,它们的体积相等.
6.判断对错.
两个体积相等的正方体,它们的棱长一定相等.
7.判断题.
一个正方体的棱长扩大2倍,体积会扩大8倍.
三、填空题
8.南岭体育场计划修一个长50米,宽20米,深2米的长方体形状的游泳池,要挖出________立方米的土。
9.一个正方体的表面积是384cm2 , 体积是________cm3 .
10.长方体或正方体底面的面积叫做________,所以长方体和正方体的体积也可以用________×________来计算。
11.把一块棱长是20cm的正方体铁坯锻压成一块长1m,宽10cm的长方体铁块,这个铁块的高是________cm
12.有甲、乙、丙三个正方体水池.它们的内棱长分别为40dm、30dm、20dm,在乙、丙水池中分别铺上碎石,两个水池的水面分别升高了6cm和6.5cm.如果将这些碎石铺在甲水池中,甲水池水面将升高________分米。
四、解答题
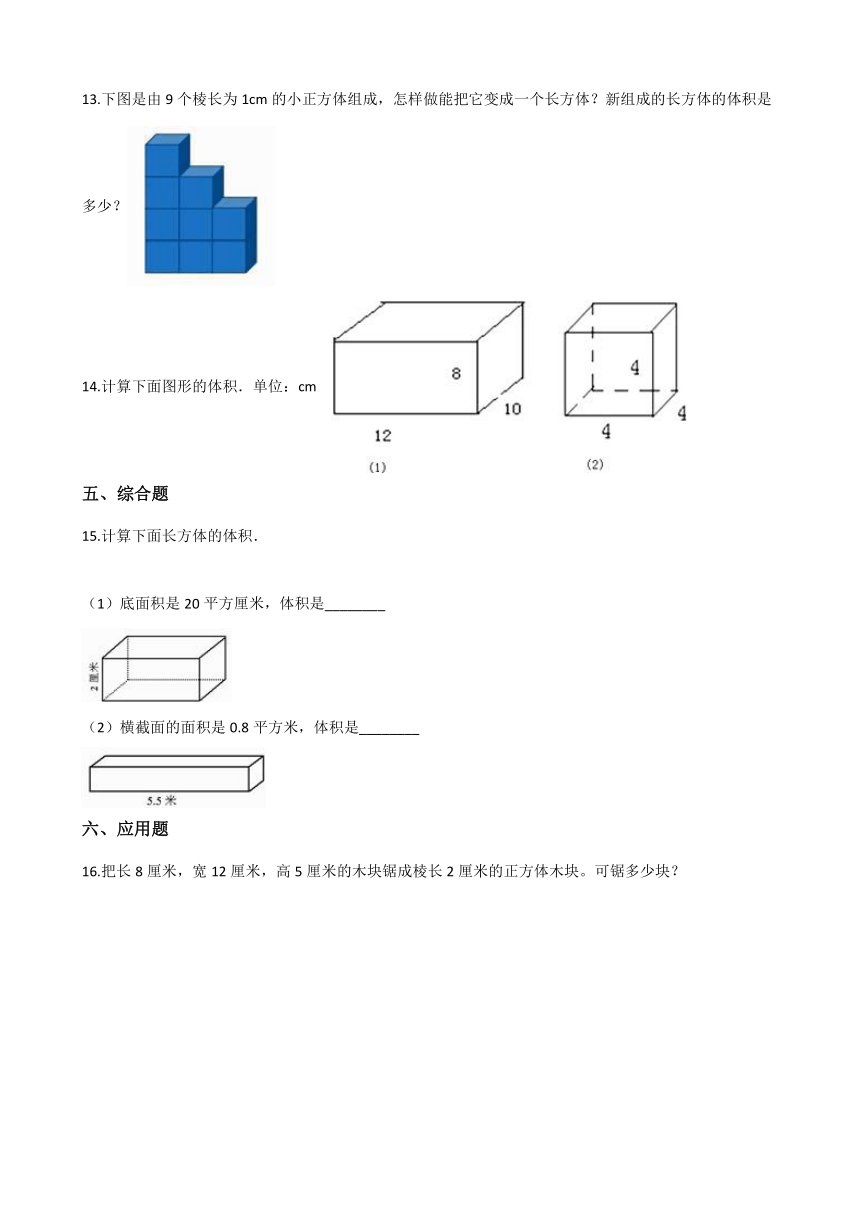
13.下图是由9个棱长为1cm的小正方体组成,怎样做能把它变成一个长方体?新组成的长方体的体积是多少?
14.计算下面图形的体积.单位:cm
五、综合题
15.计算下面长方体的体积.?
(1)底面积是20平方厘米,体积是________
(2)横截面的面积是0.8平方米,体积是________
六、应用题
16.把长8厘米,宽12厘米,高5厘米的木块锯成棱长2厘米的正方体木块。可锯多少块?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】15×6×0.74
=90×0.74
=66.6(千克)
故答案为:A.
【分析】已知长方体的底面积和高,求体积,用底面积×高=长方体的体积,然后用每升汽油的质量×油桶的容积=油桶可以装的汽油质量,据此解答.
2.【答案】C
【解析】【解答】长方体一共有6个面,分为三组:上面和下面,左面和右面,前面和后面。
【分析】大多数情况下,长宽高是不相等的,那么长方体的6个面,都是长方形,有时候会出现长宽高之中,有两个量是相等的,那么就会出现两个正方形和4个长方形,特殊情况下,长宽高都是相等的,这是长方体的一种特殊情况,正方体,那么这时,6个面都是正方形。
3.【答案】 C
【解析】【解答】正方体的体积=棱长×棱长×棱长
【分析】(棱长÷3)×(棱长÷3)×(棱长÷3)
=棱长×棱长×棱长÷27
如果每条棱都缩小了3倍,体积缩小的倍数是3的立方。
4.【答案】 C
【解析】【解答】长方体的长宽高分别是6厘米,3厘米,3厘米
表面积=(6×3+6×3+3×3)×2=90(平方厘米)
【分析】长方体见右图所示,它可以切成两个棱长是3厘米的正方体,那说明长方体的长宽高分别是6厘米,3厘米,3厘米,带入公式“长方形的表面积=(长×宽+长×高+宽×高)×2”求得表面积是90平方厘米
二、判断题
5.【答案】正确
【解析】【解答】根据分析可知,棱长之和相等的两个正方体,它们的体积相等,原题说法正确.
故答案为:正确.
【分析】正方体的棱长总和=棱长×12,棱长之和相等的两个正方体,它们的棱长相等,由正方体的体积=棱长×棱长×棱长,则它们的体积也相等.
6.【答案】正确
【解析】【解答】两个体积相等的正方体,它们的棱长一定相等.正确
故答案为:正确
【分析】正方体体积=棱长×棱长×棱长,所以两个体积相等的正方体,它们的棱长一定相等.
7.【答案】正确
【解析】【解答】根据正方体的体积公式判断,一个正方体的棱长扩大2倍,体积会扩大:2×2×2=8;原题说法正确.
故答案为:正确
【分析】正方体体积=棱长×棱长×棱长,正方体体积扩大的倍数是棱长扩大的倍数的立方倍.
三、填空题
8.【答案】2000
【解析】【解答】50×20×2
=1000×2
=2000(立方米)故答案为:2000.
【分析】根据题意,用长方体的体积=长×宽×高,据此列式解答.
9.【答案】512
【解析】【解答】解:384÷6=64(平方厘米)
64=8×8,所以正方体的棱长是8厘米.
8×8×8=512(立方厘米)
答:它的体积是512立方厘米.
故答案为:512.
【分析】根据正方体的表面积S=6a2 , 可知a2=S÷6,表面积是384平方厘米,据此可求出棱长的平方是多少,进而可求正方体的棱长,再根据正方体的体积公式:V=a3求出它的体积即可.本题的重点是根据正方体表面积计算的方法求出棱长的平方是多少,进而求出这个正方体的棱长,再根据体积公式进行计算.
10.【答案】底面积;底面积;高
【解析】【解答】解:长方体或正方体底面的面积叫做底面积,所以长方体和正方体的体积也可以用底面积×高来计算。
故答案为:底面积;底面积;高【分析】长方体的体积=长×宽×高,因为长乘宽就是长方体的底面积,所以也可以用底面积乘高来计算长方体的体积。
11.【答案】 8
【解析】【解答】1米=100厘米,20×20×20÷(100×10)=8(厘米)
【分析】首先根据正方体体积=棱长×棱长×棱长求出铁坯的体积,然后除以长方体的长和宽就是铁块的高,铁坯的体积是不变的。
12.【答案】0.5
【解析】【解答】6cm=0.6dm ??6.5cm=0.65dm
(30×30×0.6+20×20×0.65)÷(40×40)=0.5(dm)
【分析】两个水池水面上升的体积就是碎石的体积,即用两个正方体的底面积乘水升高的高度就是碎石的体积。碎石放在甲水池中,体积不变。用碎石体积除以甲池底面积,就是甲水池水面将升高的数量。
四、解答题
13.【答案】解:新组成的长方体如下图:体积是9cm?。
【解析】【分析】根据图意可知,将这个图形中的最左上方的一个正方体移动到从下向上数的第三层右边位置,即可得到一个新的长方体,新长方体的体积与原来图形的体积是相同的.
14.【答案】解:1)12×10×8 =120×8
=960(立方厘米)
答:这个长方体的体积是960立方厘米.
2)4×4×4=64(立方厘米)
答:这个正方体的体积是64立方厘米.
【解析】【分析】(1)这是一个长方体,它的长是12厘米,宽是10厘米,高是8厘米,根据长方体的体积=长×宽×高进行求解即可;(2)这是一个正方体,它的棱长是4厘米,根据正方体的体积=棱长×棱长×棱长求解即可.
五、综合题
15.【答案】(1)40立方厘米
(2)4.4立方米
【解析】【解答】解:(1)20×2=40(立方厘米);
(2)0.8×5.5=4.4(立方米)
故答案为:40立方厘米;4.4立方米
【分析】(1)用底面积乘高即可求出体积;(2)用横截面面积乘长即可求出体积.
六、应用题
16.【答案】解:长方体的高是5厘米,正方体棱长是2厘米,所以高只能锯成两层,
(8÷2)×(12÷2)×2=48(块)
答:可锯成48块.
【解析】【分析】首先明确长方体只能锯成两层棱长是2厘米的正方体,再求出长、宽能锯成的个数,用长能锯成的个数乘宽能锯成的个数求出一层的小正方体的个数,再乘层数即可解答.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-3.5问题解决
一、单选题
1.一个长方体的汽油桶,底面积是15平方分米,高是6分米,如果1升汽油重0.74千克,这个油桶可以装汽油(?? )
A.?66.6千克????????????????????????????B.?63.6千克????????????????????????????C.?6.6千克????????????????????????????D.?6.66千克
2.长方体的6个面(?? )。
A.?一定都是长方形?????????????????B.?一定都是正方形?????????????????C.?可能有长方形也可能有正方形
3.正方体的棱长缩小3倍,它的体积缩小(?? )倍。
A.?3?????????????????????????????????????????????B.?9?????????????????????????????????????????????C.?27
4.一个长方体正好可以切成两个棱长是3厘米的正方体,这个长方体的表面积是(?? )。?
A.?108平方厘米?????????????????????????????B.?54平方厘米?????????????????????????????C.?90平方厘米
二、判断题
5.判断棱长之和相等的两个正方体,它们的体积相等.
6.判断对错.
两个体积相等的正方体,它们的棱长一定相等.
7.判断题.
一个正方体的棱长扩大2倍,体积会扩大8倍.
三、填空题
8.南岭体育场计划修一个长50米,宽20米,深2米的长方体形状的游泳池,要挖出________立方米的土。
9.一个正方体的表面积是384cm2 , 体积是________cm3 .
10.长方体或正方体底面的面积叫做________,所以长方体和正方体的体积也可以用________×________来计算。
11.把一块棱长是20cm的正方体铁坯锻压成一块长1m,宽10cm的长方体铁块,这个铁块的高是________cm
12.有甲、乙、丙三个正方体水池.它们的内棱长分别为40dm、30dm、20dm,在乙、丙水池中分别铺上碎石,两个水池的水面分别升高了6cm和6.5cm.如果将这些碎石铺在甲水池中,甲水池水面将升高________分米。
四、解答题
13.下图是由9个棱长为1cm的小正方体组成,怎样做能把它变成一个长方体?新组成的长方体的体积是多少?
14.计算下面图形的体积.单位:cm
五、综合题
15.计算下面长方体的体积.?
(1)底面积是20平方厘米,体积是________
(2)横截面的面积是0.8平方米,体积是________
六、应用题
16.把长8厘米,宽12厘米,高5厘米的木块锯成棱长2厘米的正方体木块。可锯多少块?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】15×6×0.74
=90×0.74
=66.6(千克)
故答案为:A.
【分析】已知长方体的底面积和高,求体积,用底面积×高=长方体的体积,然后用每升汽油的质量×油桶的容积=油桶可以装的汽油质量,据此解答.
2.【答案】C
【解析】【解答】长方体一共有6个面,分为三组:上面和下面,左面和右面,前面和后面。
【分析】大多数情况下,长宽高是不相等的,那么长方体的6个面,都是长方形,有时候会出现长宽高之中,有两个量是相等的,那么就会出现两个正方形和4个长方形,特殊情况下,长宽高都是相等的,这是长方体的一种特殊情况,正方体,那么这时,6个面都是正方形。
3.【答案】 C
【解析】【解答】正方体的体积=棱长×棱长×棱长
【分析】(棱长÷3)×(棱长÷3)×(棱长÷3)
=棱长×棱长×棱长÷27
如果每条棱都缩小了3倍,体积缩小的倍数是3的立方。
4.【答案】 C
【解析】【解答】长方体的长宽高分别是6厘米,3厘米,3厘米
表面积=(6×3+6×3+3×3)×2=90(平方厘米)
【分析】长方体见右图所示,它可以切成两个棱长是3厘米的正方体,那说明长方体的长宽高分别是6厘米,3厘米,3厘米,带入公式“长方形的表面积=(长×宽+长×高+宽×高)×2”求得表面积是90平方厘米
二、判断题
5.【答案】正确
【解析】【解答】根据分析可知,棱长之和相等的两个正方体,它们的体积相等,原题说法正确.
故答案为:正确.
【分析】正方体的棱长总和=棱长×12,棱长之和相等的两个正方体,它们的棱长相等,由正方体的体积=棱长×棱长×棱长,则它们的体积也相等.
6.【答案】正确
【解析】【解答】两个体积相等的正方体,它们的棱长一定相等.正确
故答案为:正确
【分析】正方体体积=棱长×棱长×棱长,所以两个体积相等的正方体,它们的棱长一定相等.
7.【答案】正确
【解析】【解答】根据正方体的体积公式判断,一个正方体的棱长扩大2倍,体积会扩大:2×2×2=8;原题说法正确.
故答案为:正确
【分析】正方体体积=棱长×棱长×棱长,正方体体积扩大的倍数是棱长扩大的倍数的立方倍.
三、填空题
8.【答案】2000
【解析】【解答】50×20×2
=1000×2
=2000(立方米)故答案为:2000.
【分析】根据题意,用长方体的体积=长×宽×高,据此列式解答.
9.【答案】512
【解析】【解答】解:384÷6=64(平方厘米)
64=8×8,所以正方体的棱长是8厘米.
8×8×8=512(立方厘米)
答:它的体积是512立方厘米.
故答案为:512.
【分析】根据正方体的表面积S=6a2 , 可知a2=S÷6,表面积是384平方厘米,据此可求出棱长的平方是多少,进而可求正方体的棱长,再根据正方体的体积公式:V=a3求出它的体积即可.本题的重点是根据正方体表面积计算的方法求出棱长的平方是多少,进而求出这个正方体的棱长,再根据体积公式进行计算.
10.【答案】底面积;底面积;高
【解析】【解答】解:长方体或正方体底面的面积叫做底面积,所以长方体和正方体的体积也可以用底面积×高来计算。
故答案为:底面积;底面积;高【分析】长方体的体积=长×宽×高,因为长乘宽就是长方体的底面积,所以也可以用底面积乘高来计算长方体的体积。
11.【答案】 8
【解析】【解答】1米=100厘米,20×20×20÷(100×10)=8(厘米)
【分析】首先根据正方体体积=棱长×棱长×棱长求出铁坯的体积,然后除以长方体的长和宽就是铁块的高,铁坯的体积是不变的。
12.【答案】0.5
【解析】【解答】6cm=0.6dm ??6.5cm=0.65dm
(30×30×0.6+20×20×0.65)÷(40×40)=0.5(dm)
【分析】两个水池水面上升的体积就是碎石的体积,即用两个正方体的底面积乘水升高的高度就是碎石的体积。碎石放在甲水池中,体积不变。用碎石体积除以甲池底面积,就是甲水池水面将升高的数量。
四、解答题
13.【答案】解:新组成的长方体如下图:体积是9cm?。
【解析】【分析】根据图意可知,将这个图形中的最左上方的一个正方体移动到从下向上数的第三层右边位置,即可得到一个新的长方体,新长方体的体积与原来图形的体积是相同的.
14.【答案】解:1)12×10×8 =120×8
=960(立方厘米)
答:这个长方体的体积是960立方厘米.
2)4×4×4=64(立方厘米)
答:这个正方体的体积是64立方厘米.
【解析】【分析】(1)这是一个长方体,它的长是12厘米,宽是10厘米,高是8厘米,根据长方体的体积=长×宽×高进行求解即可;(2)这是一个正方体,它的棱长是4厘米,根据正方体的体积=棱长×棱长×棱长求解即可.
五、综合题
15.【答案】(1)40立方厘米
(2)4.4立方米
【解析】【解答】解:(1)20×2=40(立方厘米);
(2)0.8×5.5=4.4(立方米)
故答案为:40立方厘米;4.4立方米
【分析】(1)用底面积乘高即可求出体积;(2)用横截面面积乘长即可求出体积.
六、应用题
16.【答案】解:长方体的高是5厘米,正方体棱长是2厘米,所以高只能锯成两层,
(8÷2)×(12÷2)×2=48(块)
答:可锯成48块.
【解析】【分析】首先明确长方体只能锯成两层棱长是2厘米的正方体,再求出长、宽能锯成的个数,用长能锯成的个数乘宽能锯成的个数求出一层的小正方体的个数,再乘层数即可解答.
