26.2.3 用概率解说游戏的公平性(自主预习+课后集训+答案)
文档属性
| 名称 | 26.2.3 用概率解说游戏的公平性(自主预习+课后集训+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 00:00:00 | ||
图片预览



文档简介
沪科版数学九年级下册同步课时训练
第26章 概率初步
26.2 等可能情形下的概率计算
第3课时 用概率解说游戏的公平性
要点测评 基础达标
要点1 利用概率考察游戏的公平性
1. 小明和小丽做掷硬币(质量均匀)游戏.规则是:连掷四次硬币,当其中有三次结果相同时,小明获胜;当恰有两次结果相同时,小丽获胜,其他情况不计输赢.则这个规则对 有利.?
2. 甲、乙两人玩抽扑克牌游戏,游戏规则是:从牌面数字分别为5,6,7的三张扑克牌中,随机抽取一张,放回后,再随机抽取一张.若所抽的两张牌面数字的积为奇数,则甲获胜;若所抽的两张牌面数字的积为偶数,则乙获胜.这个游戏 .(填“公平”或“不公平”)
3. 如图,有A,B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
记S=x+y.
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:当S<6时甲获胜,否则乙获胜.你认为这个游戏公平吗?对谁有利?
4. 一个盒子里有标号分别为1,2,3,4,5,6的六个小球,这些小球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙羸.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
要点2 利用概率修改不公平的游戏规则
5. 一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个(分别标有1号、2号),黄球1个,从中任意摸出1球是绿球的概率是 .
(1)试求口袋中绿球的个数;
(2)小明和小刚玩摸球游戏:第一次从口袋中任意摸出1球(不放回),第二次再摸出1球.两人约定游戏胜负规则如下:摸出“一绿一黄”,则小明赢;摸出“一红一黄”,则小刚赢.你认为这种游戏胜负规则公平吗?请用列表或画树状图的方法说明理由;若你认为不公平,请修改游戏胜负规则,使游戏变得公平.
6. 有一个摸球游戏:将红、黄、蓝三个除颜色外完全相同的小球放入不透明的盒子中,游戏者从中随机摸出一球,记下颜色后放回盒中,充分摇匀,再随机摸出一球并记下颜色.游戏规则是:如果摸得的两球颜色相同,那么游戏者获胜;否则,游戏者失败.这是一个公平的游戏吗?若公平,请说明理由;若不公平,请修改规则,使之成为一个公平的游戏.
课后集训 巩固提升
7. 在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A. 三边中线的交点 B. 三边垂直平分线的交点
C. 三条角平分线的交点 D. 三边上高的交点
8. 小明和小亮做游戏,先是各自背着双方在纸上写一个正整数,然后都拿给对方看,他们约定:若两个人所写的数都是奇数或都是偶数,则小明胜,若两个人所写的数一个是奇数,另一个是偶数,则小亮获胜,这个游戏( )
A. 对小明有利 B. 对小亮有利
C. 公平 D. 无法确定
9. 小宏和小倩抛硬币游戏,规定:将一枚硬币连抛三次,若三次正面都朝上则小宏胜,若三次中只有一次正面朝上则小倩胜,你认为这种游戏公平吗( )
A. 公平 B. 小倩胜的可能大
C. 小宏胜的可能大 D. 以上答案都错
10. 某口袋中有20个球,其中白球x个,绿球2x个,其余为黑球.甲从袋中任意摸出一个球,若为绿球获胜.甲摸出的球放回袋中后,乙再从袋中摸出一个球,若为黑球则获胜.要想游戏对甲乙双方公平则x为( )
A. 3 B. 4 C. 5 D. 6
11. 小明与小刚一起玩抛掷两枚硬币的游戏,游戏规则:
抛出两个正面,则小明赢1分;抛出其他结果,则小刚赢1分;
谁先到10分,谁就获胜.
这是个不公平的游戏规则,要把它修改成公平的游戏,下列做法中错误的是( )
A. 把“抛出两个正面”改为“抛出两个面相同”
B. 把“抛出其他结果”改为“抛出两个反面”
C. 把“小明赢1分”改为“小明赢3分”
D. 把“小刚赢1分”改为“小刚赢3分”
12. 某人设摊“摸彩”,只见他手持一袋内装大小、质量完全相同的3个红球,2个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得10元钱,否则顾客付给这人10元钱,请你判断一下该活动对顾客 (填“合算”或“不合算”).?
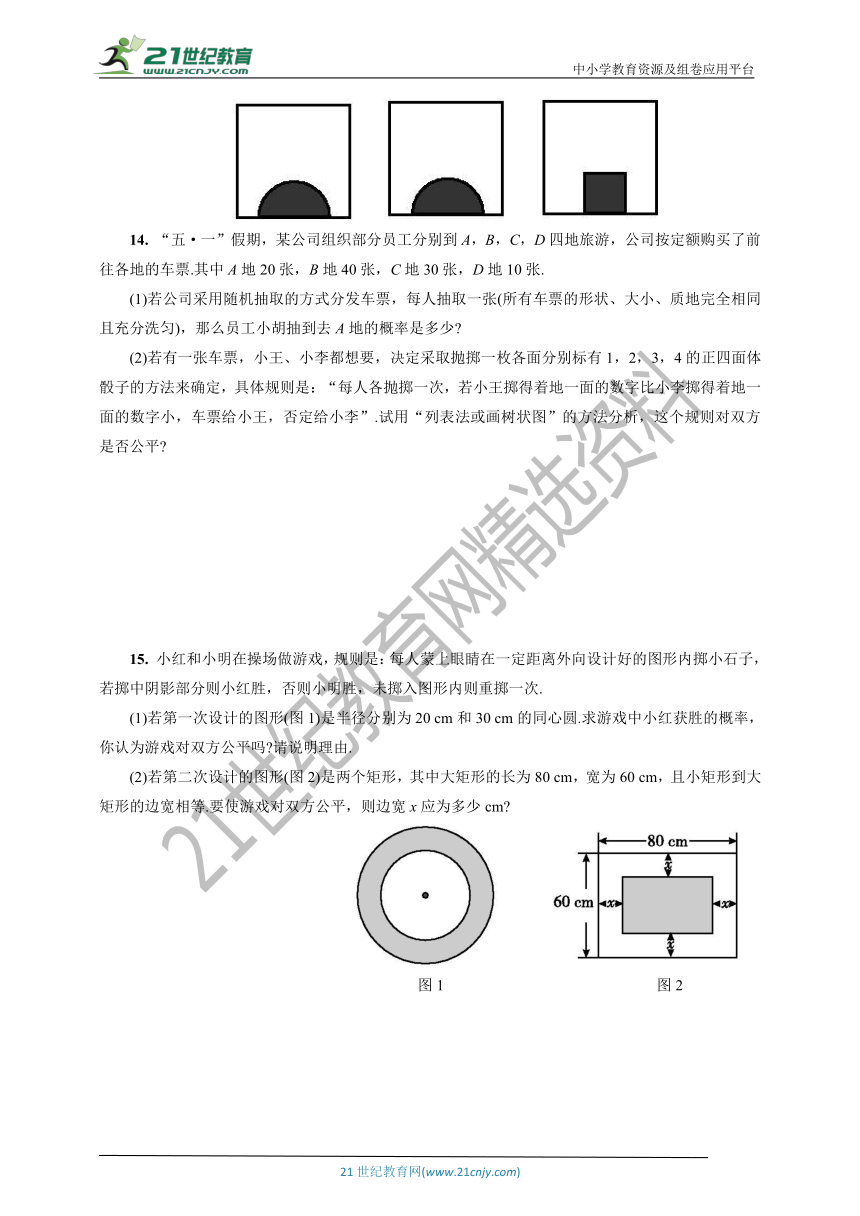
13. 如图所示,有三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形,将这三张纸片放在一个盒子里摇匀,随机地同时抽取两张纸片,若可以拼成一个圆形(即取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆,一张纸片画有正方形)则乙方赢,问甲方赢的概率是 ,此游戏 取胜的概率大.
14. “五·一”假期,某公司组织部分员工分别到A,B,C,D四地旅游,公司按定额购买了前往各地的车票.其中A地20张,B地40张,C地30张,D地10张.
(1)若公司采用随机抽取的方式分发车票,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小胡抽到去A地的概率是多少?
(2)若有一张车票,小王、小李都想要,决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小王掷得着地一面的数字比小李掷得着地一面的数字小,车票给小王,否定给小李”.试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?
15. 小红和小明在操场做游戏,规则是:每人蒙上眼睛在一定距离外向设计好的图形内掷小石子,若掷中阴影部分则小红胜,否则小明胜,未掷入图形内则重掷一次.
(1)若第一次设计的图形(图1)是半径分别为20 cm和30 cm的同心圆.求游戏中小红获胜的概率,你认为游戏对双方公平吗?请说明理由.
(2)若第二次设计的图形(图2)是两个矩形,其中大矩形的长为80 cm,宽为60 cm,且小矩形到大矩形的边宽相等.要使游戏对双方公平,则边宽x应为多少cm?
图1 图2
参 考 答 案
1. 小明 【解析】画树状图得
所以连掷四次硬币共16种等可能情况,其中有三次结果相同的有8种情况,恰有两次结果相同有6种情况,所以P(小明获胜)==,P(小丽获胜)==,所以P(小明获胜)>P(小丽获胜),所以这个规则对小明有利.
2. 不公平 【解析】画树状图如图
共有9种等可能结果,积为奇数的有4种,积为偶数的有5种,故P(甲胜)=,P(乙胜)=,因为≠,故这个游戏不公平.
3. 解:(1)列表:
y
x
2
4
6
1
(1,2)
(1,4)
(1,6)
2
(2,2)
(2,4)
(2,6)
3
(3,2)
(3,4)
(3,6)
4
(4,2)
(4,4)
(4,6)
(2)因为P(甲获胜)==,P(乙获胜)==.所以这个游戏不公平,对乙有利.
4. 解:(1)因为有标号分别为1,2,3,4,5,6六个小球,所以摸到标号数字为奇数的小球的概率为=.
(2)画树状图:如图所示,共有36种等可能的情况,两次摸到小球的标号数字同为奇数或同为偶数的有18种,摸到小球的标号数字为一奇一偶的结果有18种.
所以P(甲赢)==,P(乙赢)==,所以这个游戏对甲、乙两人是公平的.
5. 解:(1)设绿球的个数有x个.=,解得x=1.即绿球的个数为1个.
(2)画树形图如图:
共有12种等可能情况,一绿一黄的情况有2种,小明赢的概率是=;一红一黄的情况有4种情况,那么小刚赢的概率是=;所以游戏不公平;胜负规则为:摸出“一绿一黄”的情况小明赢;摸出“两红”的情况小刚赢.
6. 解:列表得:
红
黄
蓝
红
红红
黄红
蓝红
黄
红黄
黄黄
蓝黄
蓝
红蓝
黄蓝
蓝蓝
共有9种等可能情况,两球颜色相同的有3种,颜色不同的有6种,所以游戏者获胜的概率为=,游戏者失败的概率为=,因为≠,所以不公平.
可以修改为:若两球颜色相同时,游戏者得6分,不同时游戏者得3分,这样就是一个公平的游戏了.
7. B 【解析】因为三角形的三条垂直平分线的交点到三角形三个顶点的距离相等,所以凳子应放在△ABC的三条垂直平分线的交点最适当.故选B.
8. C 【解析】小明和小亮所写的数共有四种结果:“偶偶,偶奇,奇奇,奇偶”,所以两个都是奇数或偶数的概率是=,两个数一个是奇数,一个是偶数的概率是=.故选C.
9. B 【解析】画树状图,如图所示:
所有等可能的情况数有8种,其中三次正面都朝上的有1种情况,只有一次正面朝上的情况有3种,所以P(小宏获胜)=,P(小倩获胜)=,因为<,则该游戏不公平,小倩胜的可能大.故选B.
10. B 【解析】根据题意得=,即2x=20-x-2x,解得x=4.故选B.
11. D 【解析】画树状图得,
因为P(正,正)=,则出现其他结果的概率为.D选项中,小明平均得分,小刚平均得×3=分,显然不公平.故选D.
12. 不合算 【解析】画树状图得,
共有20种等可能的结果,两球的颜色相同的有8种情况,所以P(顾客得10元钱)==,P(顾客付给这人10元钱)==,因为P(顾客得10元钱)13. 乙 【解析】根据游戏规则可知,从三张大小相同的纸片中随机地同时抽取两张纸片,共3种情况:可以拼成一个圆形的有1种,可以拼成一个蘑菇形有2种,故乙取胜的概率大于甲取胜的概率,故这个游戏不公平,且甲方赢的概率是.
14. 解:(1)小胡抽到去A地的概率为=.
(2)不公平.画树状图法说明(如图),
由此可知,共有16种等可能结果.其中小王掷得数字比小李掷得数字小的有6种,所以小王掷得数字比小李掷得数字小的概率为=.则小王掷得数字不小于小李掷得数字的概率为1-=,≠,所以不公平.
15. 解:根据题意得,小红获胜的概率就是阴影部分面积与总面积的比值,小明获胜的概率就是阴影之外的部分面积与总面积的比值.
(1)P(小红获胜)=,P(小明获胜)=,所以游戏对双方不公平.
(2)根据题意可得(80-2x)(60-2x)=2 400,即x2-70x+600=0,所以x1=10,x2=60(不符合题意,舍去)所以边宽x为10 cm时,游戏对双方公平.
第26章 概率初步
26.2 等可能情形下的概率计算
第3课时 用概率解说游戏的公平性
要点测评 基础达标
要点1 利用概率考察游戏的公平性
1. 小明和小丽做掷硬币(质量均匀)游戏.规则是:连掷四次硬币,当其中有三次结果相同时,小明获胜;当恰有两次结果相同时,小丽获胜,其他情况不计输赢.则这个规则对 有利.?
2. 甲、乙两人玩抽扑克牌游戏,游戏规则是:从牌面数字分别为5,6,7的三张扑克牌中,随机抽取一张,放回后,再随机抽取一张.若所抽的两张牌面数字的积为奇数,则甲获胜;若所抽的两张牌面数字的积为偶数,则乙获胜.这个游戏 .(填“公平”或“不公平”)
3. 如图,有A,B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
记S=x+y.
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:当S<6时甲获胜,否则乙获胜.你认为这个游戏公平吗?对谁有利?
4. 一个盒子里有标号分别为1,2,3,4,5,6的六个小球,这些小球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙羸.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
要点2 利用概率修改不公平的游戏规则
5. 一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个(分别标有1号、2号),黄球1个,从中任意摸出1球是绿球的概率是 .
(1)试求口袋中绿球的个数;
(2)小明和小刚玩摸球游戏:第一次从口袋中任意摸出1球(不放回),第二次再摸出1球.两人约定游戏胜负规则如下:摸出“一绿一黄”,则小明赢;摸出“一红一黄”,则小刚赢.你认为这种游戏胜负规则公平吗?请用列表或画树状图的方法说明理由;若你认为不公平,请修改游戏胜负规则,使游戏变得公平.
6. 有一个摸球游戏:将红、黄、蓝三个除颜色外完全相同的小球放入不透明的盒子中,游戏者从中随机摸出一球,记下颜色后放回盒中,充分摇匀,再随机摸出一球并记下颜色.游戏规则是:如果摸得的两球颜色相同,那么游戏者获胜;否则,游戏者失败.这是一个公平的游戏吗?若公平,请说明理由;若不公平,请修改规则,使之成为一个公平的游戏.
课后集训 巩固提升
7. 在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A. 三边中线的交点 B. 三边垂直平分线的交点
C. 三条角平分线的交点 D. 三边上高的交点
8. 小明和小亮做游戏,先是各自背着双方在纸上写一个正整数,然后都拿给对方看,他们约定:若两个人所写的数都是奇数或都是偶数,则小明胜,若两个人所写的数一个是奇数,另一个是偶数,则小亮获胜,这个游戏( )
A. 对小明有利 B. 对小亮有利
C. 公平 D. 无法确定
9. 小宏和小倩抛硬币游戏,规定:将一枚硬币连抛三次,若三次正面都朝上则小宏胜,若三次中只有一次正面朝上则小倩胜,你认为这种游戏公平吗( )
A. 公平 B. 小倩胜的可能大
C. 小宏胜的可能大 D. 以上答案都错
10. 某口袋中有20个球,其中白球x个,绿球2x个,其余为黑球.甲从袋中任意摸出一个球,若为绿球获胜.甲摸出的球放回袋中后,乙再从袋中摸出一个球,若为黑球则获胜.要想游戏对甲乙双方公平则x为( )
A. 3 B. 4 C. 5 D. 6
11. 小明与小刚一起玩抛掷两枚硬币的游戏,游戏规则:
抛出两个正面,则小明赢1分;抛出其他结果,则小刚赢1分;
谁先到10分,谁就获胜.
这是个不公平的游戏规则,要把它修改成公平的游戏,下列做法中错误的是( )
A. 把“抛出两个正面”改为“抛出两个面相同”
B. 把“抛出其他结果”改为“抛出两个反面”
C. 把“小明赢1分”改为“小明赢3分”
D. 把“小刚赢1分”改为“小刚赢3分”
12. 某人设摊“摸彩”,只见他手持一袋内装大小、质量完全相同的3个红球,2个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得10元钱,否则顾客付给这人10元钱,请你判断一下该活动对顾客 (填“合算”或“不合算”).?
13. 如图所示,有三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形,将这三张纸片放在一个盒子里摇匀,随机地同时抽取两张纸片,若可以拼成一个圆形(即取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆,一张纸片画有正方形)则乙方赢,问甲方赢的概率是 ,此游戏 取胜的概率大.
14. “五·一”假期,某公司组织部分员工分别到A,B,C,D四地旅游,公司按定额购买了前往各地的车票.其中A地20张,B地40张,C地30张,D地10张.
(1)若公司采用随机抽取的方式分发车票,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小胡抽到去A地的概率是多少?
(2)若有一张车票,小王、小李都想要,决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小王掷得着地一面的数字比小李掷得着地一面的数字小,车票给小王,否定给小李”.试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?
15. 小红和小明在操场做游戏,规则是:每人蒙上眼睛在一定距离外向设计好的图形内掷小石子,若掷中阴影部分则小红胜,否则小明胜,未掷入图形内则重掷一次.
(1)若第一次设计的图形(图1)是半径分别为20 cm和30 cm的同心圆.求游戏中小红获胜的概率,你认为游戏对双方公平吗?请说明理由.
(2)若第二次设计的图形(图2)是两个矩形,其中大矩形的长为80 cm,宽为60 cm,且小矩形到大矩形的边宽相等.要使游戏对双方公平,则边宽x应为多少cm?
图1 图2
参 考 答 案
1. 小明 【解析】画树状图得
所以连掷四次硬币共16种等可能情况,其中有三次结果相同的有8种情况,恰有两次结果相同有6种情况,所以P(小明获胜)==,P(小丽获胜)==,所以P(小明获胜)>P(小丽获胜),所以这个规则对小明有利.
2. 不公平 【解析】画树状图如图
共有9种等可能结果,积为奇数的有4种,积为偶数的有5种,故P(甲胜)=,P(乙胜)=,因为≠,故这个游戏不公平.
3. 解:(1)列表:
y
x
2
4
6
1
(1,2)
(1,4)
(1,6)
2
(2,2)
(2,4)
(2,6)
3
(3,2)
(3,4)
(3,6)
4
(4,2)
(4,4)
(4,6)
(2)因为P(甲获胜)==,P(乙获胜)==.所以这个游戏不公平,对乙有利.
4. 解:(1)因为有标号分别为1,2,3,4,5,6六个小球,所以摸到标号数字为奇数的小球的概率为=.
(2)画树状图:如图所示,共有36种等可能的情况,两次摸到小球的标号数字同为奇数或同为偶数的有18种,摸到小球的标号数字为一奇一偶的结果有18种.
所以P(甲赢)==,P(乙赢)==,所以这个游戏对甲、乙两人是公平的.
5. 解:(1)设绿球的个数有x个.=,解得x=1.即绿球的个数为1个.
(2)画树形图如图:
共有12种等可能情况,一绿一黄的情况有2种,小明赢的概率是=;一红一黄的情况有4种情况,那么小刚赢的概率是=;所以游戏不公平;胜负规则为:摸出“一绿一黄”的情况小明赢;摸出“两红”的情况小刚赢.
6. 解:列表得:
红
黄
蓝
红
红红
黄红
蓝红
黄
红黄
黄黄
蓝黄
蓝
红蓝
黄蓝
蓝蓝
共有9种等可能情况,两球颜色相同的有3种,颜色不同的有6种,所以游戏者获胜的概率为=,游戏者失败的概率为=,因为≠,所以不公平.
可以修改为:若两球颜色相同时,游戏者得6分,不同时游戏者得3分,这样就是一个公平的游戏了.
7. B 【解析】因为三角形的三条垂直平分线的交点到三角形三个顶点的距离相等,所以凳子应放在△ABC的三条垂直平分线的交点最适当.故选B.
8. C 【解析】小明和小亮所写的数共有四种结果:“偶偶,偶奇,奇奇,奇偶”,所以两个都是奇数或偶数的概率是=,两个数一个是奇数,一个是偶数的概率是=.故选C.
9. B 【解析】画树状图,如图所示:
所有等可能的情况数有8种,其中三次正面都朝上的有1种情况,只有一次正面朝上的情况有3种,所以P(小宏获胜)=,P(小倩获胜)=,因为<,则该游戏不公平,小倩胜的可能大.故选B.
10. B 【解析】根据题意得=,即2x=20-x-2x,解得x=4.故选B.
11. D 【解析】画树状图得,
因为P(正,正)=,则出现其他结果的概率为.D选项中,小明平均得分,小刚平均得×3=分,显然不公平.故选D.
12. 不合算 【解析】画树状图得,
共有20种等可能的结果,两球的颜色相同的有8种情况,所以P(顾客得10元钱)==,P(顾客付给这人10元钱)==,因为P(顾客得10元钱)
14. 解:(1)小胡抽到去A地的概率为=.
(2)不公平.画树状图法说明(如图),
由此可知,共有16种等可能结果.其中小王掷得数字比小李掷得数字小的有6种,所以小王掷得数字比小李掷得数字小的概率为=.则小王掷得数字不小于小李掷得数字的概率为1-=,≠,所以不公平.
15. 解:根据题意得,小红获胜的概率就是阴影部分面积与总面积的比值,小明获胜的概率就是阴影之外的部分面积与总面积的比值.
(1)P(小红获胜)=,P(小明获胜)=,所以游戏对双方不公平.
(2)根据题意可得(80-2x)(60-2x)=2 400,即x2-70x+600=0,所以x1=10,x2=60(不符合题意,舍去)所以边宽x为10 cm时,游戏对双方公平.
