六年级上册数学试题-第三单元达标作业 冀教版(含答案)
文档属性
| 名称 | 六年级上册数学试题-第三单元达标作业 冀教版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 754.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 12:04:50 | ||
图片预览

文档简介
第三单元达标作业
一、仔细想,认真填。
1.圆柱的侧面沿一条高展开后是一个( )形或( )形,如果展开后是一个( )形,那么这个圆柱的底面周长和高相等。
2.一个圆柱的体积是125.6 cm?,高是10 cm,它的底面半径是( )cm。
3.一个圆柱的底面周长是18.84 cm,高是4 cm,它的侧面积是( )cm?,表面积是( )cm?,体积是( ) cm?。
4.圆柱的体积不变,如果底面积扩大到原来的3倍,高应该( )。
5.一根长26 dm的圆柱形钢材被切成3个大小相同的小圆柱,表面积比原来增加了48 dm?,这根钢材原来的体积是( )dm?。
6.把一根圆柱形木料削成一个与其等底等高的圆锥.削去部分的体积是4.2 dm?,原来圆柱形木料的体积是( )dm?,圆锥的体积是( )dm?。
二、精挑细选。(将正确答案的序号填在括号里)
1.一个圆柱和一个圆锥等底等高,它们的体积之和是52 dm?,那么这个圆柱的体积是( )dm?。
A.13
B.26
C.39
D.无法确定
2.一根圆柱形木料,底面半径是4 dm,高是8 dm。把这根木料沿高锯成相等的两部分
后,表面积比原来增加( )dm?。
A.8
B.32
C.64
D.128
3.下图中圆锥的体积与圆柱( )的体积相等。
A B C D
4.一个圆锥的体积是15 dm?,底面积是5 dm?,高是( )dm。
A.3
B.9
C.15
D.27
5.圆柱的底面半径和高都扩大到原来的2倍,则它的体积将扩大到原来的( )。
A.不变
B.2倍
C.4倍
D.8倍
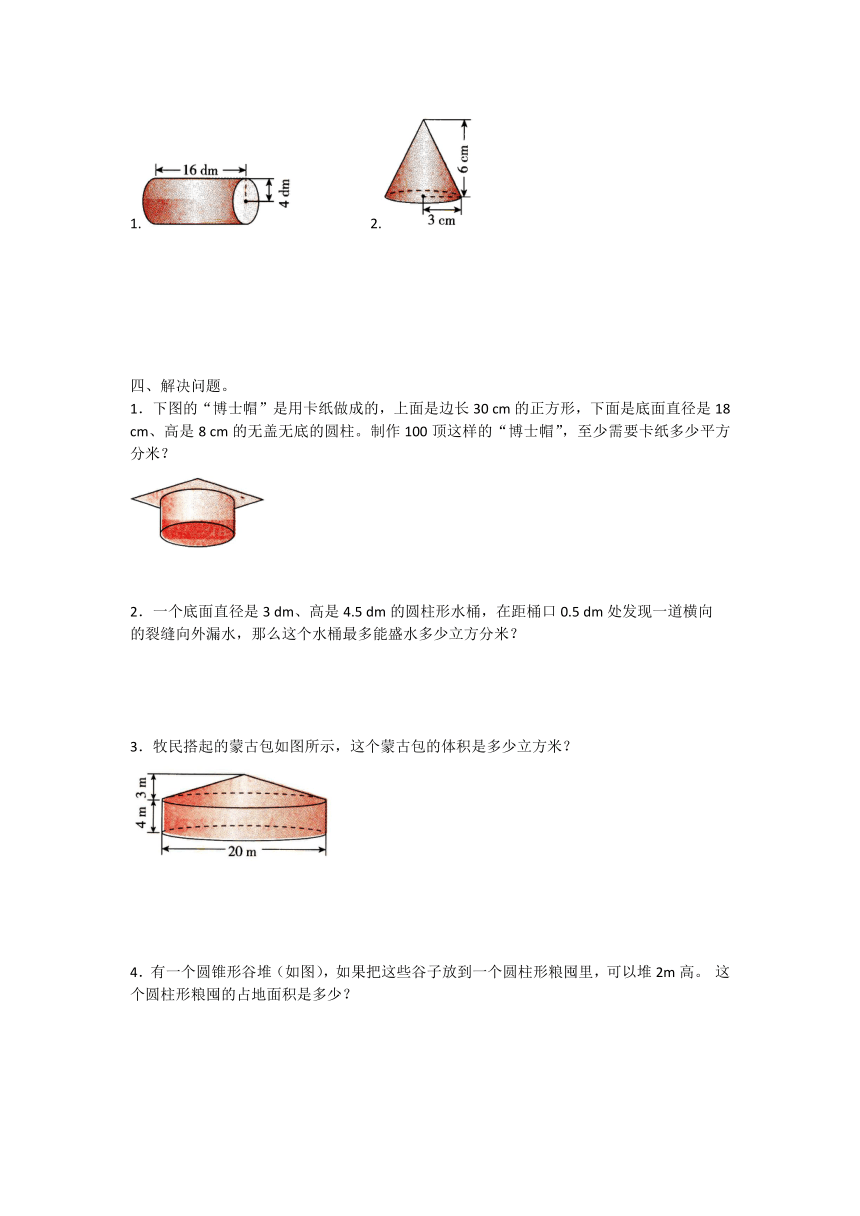
三、计算下面各图形的体积。
1. 2.
四、解决问题。
1.下图的“博士帽”是用卡纸做成的,上面是边长30 cm的正方形,下面是底面直径是18 cm、高是8 cm的无盖无底的圆柱。制作100顶这样的“博士帽”,至少需要卡纸多少平方分米?
2.一个底面直径是3 dm、高是4.5 dm的圆柱形水桶,在距桶口0.5 dm处发现一道横向
的裂缝向外漏水,那么这个水桶最多能盛水多少立方分米?
3.牧民搭起的蒙古包如图所示,这个蒙古包的体积是多少立方米?
4.有一个圆锥形谷堆(如图),如果把这些谷子放到一个圆柱形粮囤里,可以堆2m高。 这个圆柱形粮囤的占地面积是多少?
5.一个药瓶,它的瓶身呈圆柱形(不包括瓶颈).如下图所示。它的容积为26.4 cm?。瓶子正放时,瓶内药水液面高6 cm.瓶子倒放时,空余部分高2 cm,则瓶内药水的体积是多少立方厘米?
第三单元达标作业
一、1.长方 正方 正方
解析 当圆柱的底面周长等于高时,沿高展开后的图形为正方形。
2
解析 根据圆柱的体积公式,可以得出圆柱的底面半径。r?=125.6÷10÷3.14=4(cm?),即r=2 cm。
3. 75.36 131.88 113.04
解析 由圆柱的底面周长可求出底面半径:r=C÷π÷2=3(cm),根据“圆柱侧面积=底面周长×高,圆柱表面积=侧面积+底面积×2,圆柱体积=底面积×高”可分别求出圆柱的侧面积、表面积、体积。
4.缩小到原来的
解析 根据圆柱的体积公式:V=Sh,可知底面积扩大到原来的3倍,要使圆柱的体积不变,高应该缩小到原来的.
5. 312
解析 把圆柱形钢材切成3段后,增加了4个底面的面积,一个底面的面积=48÷4=12(dm?)。已知底面积和高,可求得圆柱形钢材的体积。
6. 6.3 2.1
解析 因为圆柱体积等于与它等底等高的圆锥体积的3倍,把圆柱削成圆锥,削去部分的体积是圆锥体积的2倍,所以圆锥体积为4.2÷2=2.1(dm?),圆柱体积为2.1×3=6.3(dm?)。
二、1.C
解析 圆柱与圆锥等底等高,那么圆柱体积是圆锥体积的3倍,它们的体积之和是52 dm?,则圆锥体积的4倍是52 dm?,圆锥体积为52÷4=13 (dm?),圆柱体积为13×3=39(dm?)。
2.D
解析 把木料沿高锯成相等的两部分后,表面积增加的部分为两个正方形,正方形的边长是圆柱的底面直径(或圆柱的高),所以一个正方形的面积为8×8=64(dm?),增加的表面积为64×2=128(dm?)。
3.C
解析 等底等高的圆锥体积是圆柱体积的,若圆锥与圆柱体积相等,要么圆锥的高是圆柱高的3倍,要么圆锥的底面积是圆柱的底面积的3倍。
4.B
解析 根据圆锥的体积公式“V=Sh”可推导出“h=3V÷S”,所以圆锥的高为3×15÷5=9(dm)。
5.D
解析 原圆柱的体积可以表示为,现圆柱底面半径和高都扩大到原来的2倍,此时圆柱的体积可以表示为,即。此题也可以通过设数举例的方法得到结果。
三、(1)3 .14×4 2×16 (2)3.14×3?×6×
=50.24×16 =28.26×6×
=803.84 (dm?) =56.52(cm?)
解析 根据“圆柱体积=底面积×高,圆锥体积=底面积×高×”,可分别求出圆柱、圆锥的体积。
四、1. 3.14×18×8+30×30=452.16+900=1352.16(cm?)
1352.16×100=135216(cm?)
135216 cm?=1352.16 dm?
答:至少需要卡纸1352.16 dm?。
解析 “博士帽”的顶部是一个正方形,可列算式求出面积:30×30=900(cm?);“博士帽”的顶部以下是一个无盖无底的圆柱,只要求得圆柱侧面积即可,列式为3.14×18×8=452.16( cm?)。两部分面积相加即是一顶“博士帽”所用卡纸的面积:452.16+900=1352.16(cm?),再乘100求出100顶“博士帽”需用卡纸的面积是多少。
2.3.14×(3÷2)?×(4.5-0.5)=7.065×4=28.26(dm?)
答:这个水桶最多能盛水28.26 dm?。
解析 由于距桶口0.5 dm处发现一道横向裂缝向外漏水,因此盛水高度降低0.5 dm,最高水位为4 dm,再根据圆柱体积公式计算盛水的体积。
3. 20÷2=10(m)
3.14×10?×4+3.14×10?×3×
=314×4+314×3×
=1256+314
=1570( m?)
答:这个蒙古包的体积是1570 m?。
解析 如题图所示,蒙古包由两部分组成,上半部分是底面直径为20 m、高3m的圆锥,下半部分是底面直径为20 m、高4m的圆柱,根据“圆柱体积=底面积×高,圆锥体积=底面积×高×”可分别求出圆柱、圆锥的体积。两部分体积相加即得所求蒙古包的体积。
4. 3.14×2?×1.5×=12.56×1.5×=6.28(m?)
6.28÷2=3.14(m?)
答:这个圆柱形粮囤的占地面积是3.14 m?。
解析 已知圆锥形谷堆的底面半径是2m,高是 1.5 m,根据“圆锥体积=底面积×高×”,求出谷堆的体积,列式为3.14×2?×1.5×=6.28(m?)。由“圆柱体积=底面积×高”可知“底面积=圆柱体积÷高”,列式为6.28÷2=3.14(m?)。
5. 26.4÷(6+2)=3.3(cm2)
3.3×6=19.8( cm?)
答:瓶内药水的体积是19.8 cm?。
解析 药瓶的容积可由药水体积和空余部分体积两部分组成,由于两部分的体积都可用药瓶底面积乘高求出,所以药水的体积可以表示为V=6S,空余部分的体积可以表示为V=2S,两者相加得8S,即药瓶的容积等于8S,由此可以求出底面积,再用圆柱体积公式求出药水体积。
一、仔细想,认真填。
1.圆柱的侧面沿一条高展开后是一个( )形或( )形,如果展开后是一个( )形,那么这个圆柱的底面周长和高相等。
2.一个圆柱的体积是125.6 cm?,高是10 cm,它的底面半径是( )cm。
3.一个圆柱的底面周长是18.84 cm,高是4 cm,它的侧面积是( )cm?,表面积是( )cm?,体积是( ) cm?。
4.圆柱的体积不变,如果底面积扩大到原来的3倍,高应该( )。
5.一根长26 dm的圆柱形钢材被切成3个大小相同的小圆柱,表面积比原来增加了48 dm?,这根钢材原来的体积是( )dm?。
6.把一根圆柱形木料削成一个与其等底等高的圆锥.削去部分的体积是4.2 dm?,原来圆柱形木料的体积是( )dm?,圆锥的体积是( )dm?。
二、精挑细选。(将正确答案的序号填在括号里)
1.一个圆柱和一个圆锥等底等高,它们的体积之和是52 dm?,那么这个圆柱的体积是( )dm?。
A.13
B.26
C.39
D.无法确定
2.一根圆柱形木料,底面半径是4 dm,高是8 dm。把这根木料沿高锯成相等的两部分
后,表面积比原来增加( )dm?。
A.8
B.32
C.64
D.128
3.下图中圆锥的体积与圆柱( )的体积相等。
A B C D
4.一个圆锥的体积是15 dm?,底面积是5 dm?,高是( )dm。
A.3
B.9
C.15
D.27
5.圆柱的底面半径和高都扩大到原来的2倍,则它的体积将扩大到原来的( )。
A.不变
B.2倍
C.4倍
D.8倍
三、计算下面各图形的体积。
1. 2.
四、解决问题。
1.下图的“博士帽”是用卡纸做成的,上面是边长30 cm的正方形,下面是底面直径是18 cm、高是8 cm的无盖无底的圆柱。制作100顶这样的“博士帽”,至少需要卡纸多少平方分米?
2.一个底面直径是3 dm、高是4.5 dm的圆柱形水桶,在距桶口0.5 dm处发现一道横向
的裂缝向外漏水,那么这个水桶最多能盛水多少立方分米?
3.牧民搭起的蒙古包如图所示,这个蒙古包的体积是多少立方米?
4.有一个圆锥形谷堆(如图),如果把这些谷子放到一个圆柱形粮囤里,可以堆2m高。 这个圆柱形粮囤的占地面积是多少?
5.一个药瓶,它的瓶身呈圆柱形(不包括瓶颈).如下图所示。它的容积为26.4 cm?。瓶子正放时,瓶内药水液面高6 cm.瓶子倒放时,空余部分高2 cm,则瓶内药水的体积是多少立方厘米?
第三单元达标作业
一、1.长方 正方 正方
解析 当圆柱的底面周长等于高时,沿高展开后的图形为正方形。
2
解析 根据圆柱的体积公式,可以得出圆柱的底面半径。r?=125.6÷10÷3.14=4(cm?),即r=2 cm。
3. 75.36 131.88 113.04
解析 由圆柱的底面周长可求出底面半径:r=C÷π÷2=3(cm),根据“圆柱侧面积=底面周长×高,圆柱表面积=侧面积+底面积×2,圆柱体积=底面积×高”可分别求出圆柱的侧面积、表面积、体积。
4.缩小到原来的
解析 根据圆柱的体积公式:V=Sh,可知底面积扩大到原来的3倍,要使圆柱的体积不变,高应该缩小到原来的.
5. 312
解析 把圆柱形钢材切成3段后,增加了4个底面的面积,一个底面的面积=48÷4=12(dm?)。已知底面积和高,可求得圆柱形钢材的体积。
6. 6.3 2.1
解析 因为圆柱体积等于与它等底等高的圆锥体积的3倍,把圆柱削成圆锥,削去部分的体积是圆锥体积的2倍,所以圆锥体积为4.2÷2=2.1(dm?),圆柱体积为2.1×3=6.3(dm?)。
二、1.C
解析 圆柱与圆锥等底等高,那么圆柱体积是圆锥体积的3倍,它们的体积之和是52 dm?,则圆锥体积的4倍是52 dm?,圆锥体积为52÷4=13 (dm?),圆柱体积为13×3=39(dm?)。
2.D
解析 把木料沿高锯成相等的两部分后,表面积增加的部分为两个正方形,正方形的边长是圆柱的底面直径(或圆柱的高),所以一个正方形的面积为8×8=64(dm?),增加的表面积为64×2=128(dm?)。
3.C
解析 等底等高的圆锥体积是圆柱体积的,若圆锥与圆柱体积相等,要么圆锥的高是圆柱高的3倍,要么圆锥的底面积是圆柱的底面积的3倍。
4.B
解析 根据圆锥的体积公式“V=Sh”可推导出“h=3V÷S”,所以圆锥的高为3×15÷5=9(dm)。
5.D
解析 原圆柱的体积可以表示为,现圆柱底面半径和高都扩大到原来的2倍,此时圆柱的体积可以表示为,即。此题也可以通过设数举例的方法得到结果。
三、(1)3 .14×4 2×16 (2)3.14×3?×6×
=50.24×16 =28.26×6×
=803.84 (dm?) =56.52(cm?)
解析 根据“圆柱体积=底面积×高,圆锥体积=底面积×高×”,可分别求出圆柱、圆锥的体积。
四、1. 3.14×18×8+30×30=452.16+900=1352.16(cm?)
1352.16×100=135216(cm?)
135216 cm?=1352.16 dm?
答:至少需要卡纸1352.16 dm?。
解析 “博士帽”的顶部是一个正方形,可列算式求出面积:30×30=900(cm?);“博士帽”的顶部以下是一个无盖无底的圆柱,只要求得圆柱侧面积即可,列式为3.14×18×8=452.16( cm?)。两部分面积相加即是一顶“博士帽”所用卡纸的面积:452.16+900=1352.16(cm?),再乘100求出100顶“博士帽”需用卡纸的面积是多少。
2.3.14×(3÷2)?×(4.5-0.5)=7.065×4=28.26(dm?)
答:这个水桶最多能盛水28.26 dm?。
解析 由于距桶口0.5 dm处发现一道横向裂缝向外漏水,因此盛水高度降低0.5 dm,最高水位为4 dm,再根据圆柱体积公式计算盛水的体积。
3. 20÷2=10(m)
3.14×10?×4+3.14×10?×3×
=314×4+314×3×
=1256+314
=1570( m?)
答:这个蒙古包的体积是1570 m?。
解析 如题图所示,蒙古包由两部分组成,上半部分是底面直径为20 m、高3m的圆锥,下半部分是底面直径为20 m、高4m的圆柱,根据“圆柱体积=底面积×高,圆锥体积=底面积×高×”可分别求出圆柱、圆锥的体积。两部分体积相加即得所求蒙古包的体积。
4. 3.14×2?×1.5×=12.56×1.5×=6.28(m?)
6.28÷2=3.14(m?)
答:这个圆柱形粮囤的占地面积是3.14 m?。
解析 已知圆锥形谷堆的底面半径是2m,高是 1.5 m,根据“圆锥体积=底面积×高×”,求出谷堆的体积,列式为3.14×2?×1.5×=6.28(m?)。由“圆柱体积=底面积×高”可知“底面积=圆柱体积÷高”,列式为6.28÷2=3.14(m?)。
5. 26.4÷(6+2)=3.3(cm2)
3.3×6=19.8( cm?)
答:瓶内药水的体积是19.8 cm?。
解析 药瓶的容积可由药水体积和空余部分体积两部分组成,由于两部分的体积都可用药瓶底面积乘高求出,所以药水的体积可以表示为V=6S,空余部分的体积可以表示为V=2S,两者相加得8S,即药瓶的容积等于8S,由此可以求出底面积,再用圆柱体积公式求出药水体积。
