第五章 生活中的轴对称单元测试卷(解析版)
文档属性
| 名称 | 第五章 生活中的轴对称单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 00:00:00 | ||
图片预览



文档简介
2019-2020北师大版七年级数学下册第五章生活中的轴对称单元卷解析版
一、选择题(每小题3分,共30分)
1.以下四个标志中,是轴对称图形的是(??? )
A.?????????????????B.?????????????????C.?????????????????D.?
2.下列图形中不是轴对称图形的是(?? )
A.??????????????????????????????B.?????????????????????????????C.??????????????????????????????D.?
3.如图,羊字象征吉祥和美满,如图的图案与羊有关,其中是轴对称的有( ?)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.等腰三角形的一条边长为5,另一边长为11,则它的底边长为(??? )
A.?5????????????????????????????????????????B.?11????????????????????????????????????????C.?6???????????????????????????????????????D.?5或11
5.如图,△ABC与△A′B′C′关于直线DE对称,且∠C=78°,∠B′=48°,则∠A的度数为(??? )
A.?48°???????????????????????????????????????B.?54°???????????????????????????????????????C.?74°???????????????????????????????????????D.?78°
6.如图, 周长为 ,把 的边 对折,使顶点 和点 重合,折痕交 边于点 ,交 边于点 ,连接 ,若 ,则 的周长是(?? )
A.??????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
7.等腰三角形的一个底角是 ,则它的顶角是( )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
8.如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是(?? )
A.?45°???????????????????????????????????????B.?60°???????????????????????????????????????C.?50°???????????????????????????????????????D.?55°
9.如图, 是 的角平分线, , , , 分别是垂足,若 , ,则 的长为(?? )
A.?3???????????????????????????????????????????B.?6???????????????????????????????????????????C.?9???????????????????????????????????????????D.?12
10.如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D,E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是(?? )
A.?到一个角两边距离相等的点在这个角的平分线上 B.?角平分线上的点到这个角两边的距离相等 C.?到线段两端点距离相等的点在这条线段的垂直平分线上 D.?线段垂直平分线上的点到线段两端点的距离相等
二、填空题(每小题3分,共18分)
11.已知一等腰三角形的两边长为3cm和7cm,则其腰长为________cm.
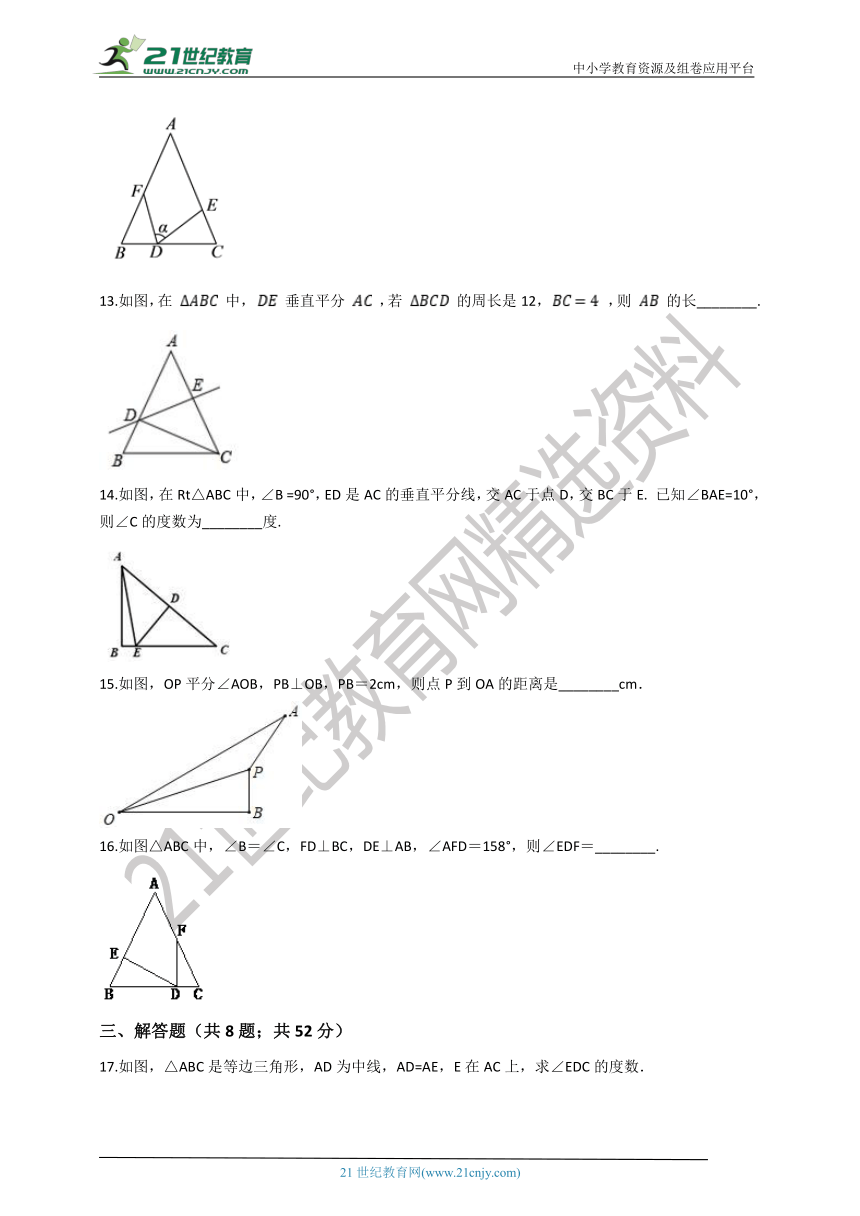
12.如图,在 中, , , , 与 的关系是________.
13.如图,在 中, 垂直平分 ,若 的周长是12, ,则 的长________.
14.如图,在Rt△ABC中,∠B =90°,ED是AC的垂直平分线,交AC于点D,交BC于E. 已知∠BAE=10°,则∠C的度数为________度.
15.如图,OP平分∠AOB,PB⊥OB,PB=2cm,则点P到OA的距离是________cm.
16.如图△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠EDF=________.
三、解答题(共8题;共52分)
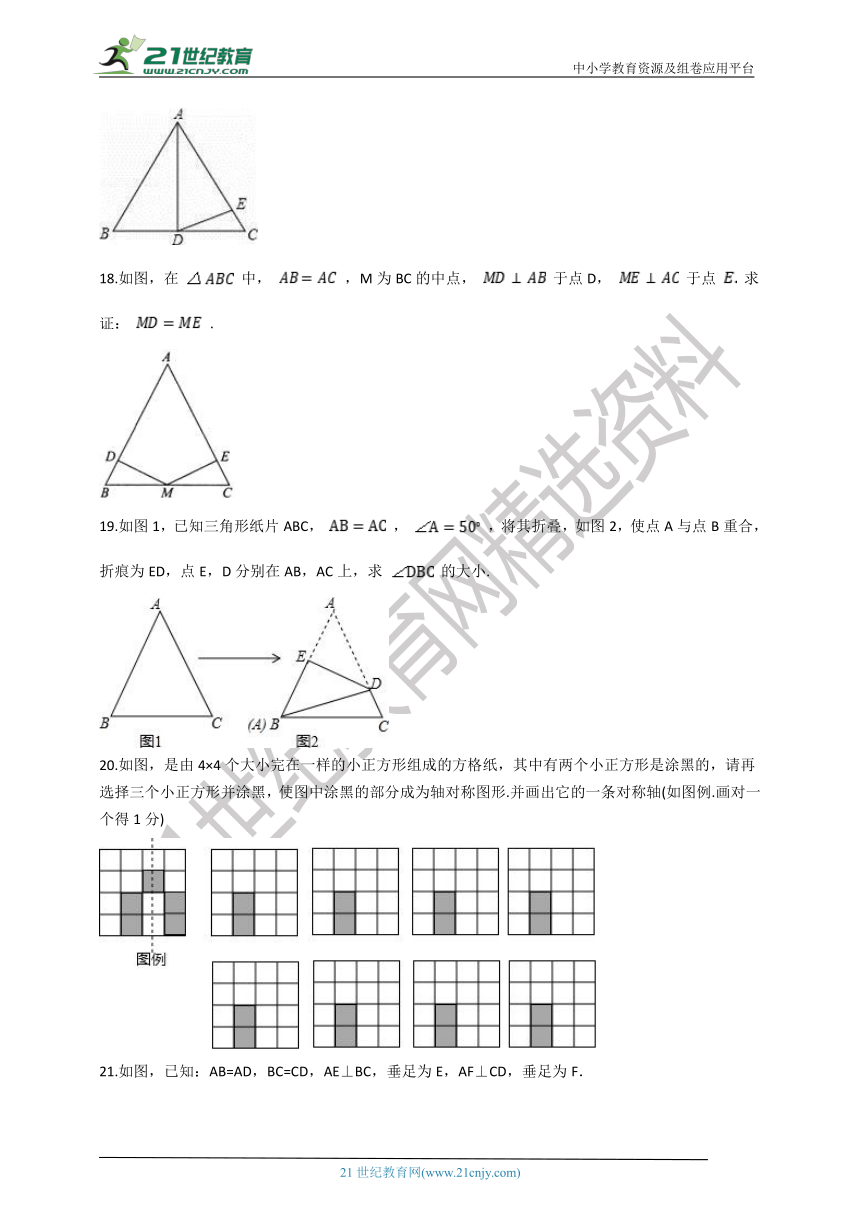
17.如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
18.如图,在 中, ,M为BC的中点, 于点D, 于点 求证: .
19.如图1,已知三角形纸片ABC, , ,将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,求 的大小.
20.如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
21.如图,已知:AB=AD,BC=CD,AE⊥BC,垂足为E,AF⊥CD,垂足为F.
求证:
(1)∠B=∠D;
(2)AE=AF.
22.如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC=________°.
23.如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.
(1)画△ABC关于直线MN的对称图形△A1B1C1不写画法 ;
(2)求△AB的面积;
24.如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O.
(1)求证:△ACE≌△DCB;
(2)求∠AOB的度数.
2019-2020北师大版七年级数学下册第五章生活中的轴对称单元卷解析版
一、选择题
1.解:A、是中心对称图形,不是轴对称图形,不符合题意; B、既不是轴对称图形也不是中心对称图形,不符合题意; C、是轴对称图形,符合题意; D、既不是轴对称图形也不是中心对称图形,不符合题意. 故答案为:C. 2.观察图形可知B、C、D都是轴对称图形,
A不是轴对称图形.
故选A.
3.解:由图可得,第一个和第二个是轴对称图形,共2个.
故答案为:B.
4.解:若等腰三角形的底边为5,则两腰长为11,这时三角形三边关系满足 ,可以组成三角形,所以成立;
若等腰三角形的底边为11,则两腰长为5,这时三角形三边关系为 ,不能组成三角形,所以不成立;
所以等腰三角形底边为5,
故答案为:A.
5.解:∵△ABC与△A′B′C′关于直线DE对称, ∴∠B=∠B′=48° ∵在△ABC中,∠C=78°,∠B=∠B′=48°, ∴∠A=180°?78°?48°=54° 故答案为:B. 6.∵△ABC的边AC对折顶点C和点A重合,
∴AE=EC,AD=CD,
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC,
∵AE=6cm,
∴AC=AE+EC=6+6=12,
∵△ABC的周长为30cm,
∴AB+BC=30?12=18cm,
∴△ABD的周长是18cm.
故答案为:B.
7.解:∵一个等腰三角形的一个底角是40°,
∴另一个底角也是40°,
∴顶角为:180°-40°×2
=180°-80°
=100°
故答案为:C.
8.解:∵MN是AE的垂直平分线,
∴AC=EC,
∴∠CAE=∠E,
∴∠ACB=∠CAE+∠E=2∠E,
∵AB=CE,
∴AC=CE, ∴∠B=∠ACB=2∠E,
在△ABC中,∠BAE+∠B+∠E=180°,
∴105°+2∠E+∠E=180°
即∠E=25°.
∴∠B=2∠E=50°.
故答案为:C.
9.解:∵ ,
∴
∴
又∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴
即AC= .
故选:A.
10.∵OD=OE,
∴O点在线段DE的垂直平分线上,
∵CD=CE,
∴C点在线段DE的垂直平分线上,
∴CO是线段DE的垂直平分线上,
∴OC⊥l.
故选:C.
二、填空题
11.等腰三角形腰长相等,该等腰三角形的三边长分别为:3,3,7或3,7,7
∵三角形两边之和大于第三边
∴该等腰三角形的腰长为7
故答案为:7
12.解:∵AB=AC,
∴∠B=∠C,
∵BF=CD,BD=CE,
∴△BDF≌△CED(SAS),
∴∠BFD=∠EDC,
∵α+∠BDF+∠EDC=180°,
∴α+∠BDF+∠BFD=180°,
∵∠B+∠BDF+∠BFD=180°,
∴∠B=α,
∴∠C=∠B=α,
∵∠A+∠B+∠C=180°,
∴2α+∠A=180°,
∴ ,
故答案为: .
13.∵DE垂直平分AC,
∴AD=CD.
∵△BCD的周长是12,BC=4,
∴AB=BD+CD=12-4=8,
故答案为:8.
14.解:∵ ED是AC的垂直平分线, ∴EA=EC, ∴∠EAC=∠ECA, 设∠EAC=x, ∵∠EAC+∠ECA+∠BAE+∠ABC=180°, 即2x+10°+90°=180°, 解得x=40°. 故答案为:40. 15.解:过点P作PD⊥OA于点D,
∵OP平分∠AOB,PB⊥OB,PB=2cm,
∴PD=PB=2cm,
故答案为2.
16.∵AB=AC
∴∠B=∠C
∵FD⊥BC于D,DE⊥AB于E
∴∠BED=∠FDC=90°,
又∵∠B=∠C,
∴∠EDB=∠CFD
∵∠AFD=158°
∴∠EDB=∠CFD=180°-158°=22°
∴∠EDF=90°-∠EDB=90°-22°=68°
三、解答题
17. 解:∵△ABC是等边三角形,AD为中线,
∴AD⊥BC,∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED= =75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
18. 证明:连接AM,如图,
在 和 中
,
≌ ,???
,
, ,???
19. 解:? ∵AB=AC, ∴∠ABC=∠ACB,
而? ∠A=50°, ∴∠ABC=(180°-50°)=65°
∵?使点A与点B重合,折痕为ED, ∴∠ABD=∠A=50°,
∴∠DBC=∠ABC-∠ABD=65°-50°=15°.
20. 解:如图所示:
21. (1)证明:在△ABC与△ADC中,
,
∴△ABC≌△ADC,
∴∠B=∠D
(2)证明:∵△ABC≌△ADC,
∴∠ACB=∠ACD,
∵AE⊥BC,垂足为E,AF⊥CD,垂足为F,
∴AE=AF
22.(1)解:∵AB=AC,
∴∠B=∠ACF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS)
(2)75
解:(2)∵△ABE≌△ACF,∠BAE=30°,
∴∠CAF=∠BAE=30°,
∵AD=AC,
∴∠ADC=∠ACD,
∴∠ADC= =75°,
故答案为:75.
23.(1)解:如图所示
(2)解:S△ABC=4×5﹣ ×1×4﹣ ×1×4﹣ ×3×5=8.5
24. (1)解:如图:AC与BD交于点H.
∵△ACD,△BCE都是等边三角形,
∴CD=CA,CB=CE,∠ACD=∠BCE=60°,
∴∠DCB=∠ACE,
在△DCB和△ACE中,
,
∴△DCB≌△ACE(SAS),
(2)解:∵△DCB≌△ACE,
∴∠CAE=∠CDB,
∵∠DCH+∠CHD+∠BDC=180°,∠AOH+∠AHO+∠CAE=180°,∠DHC=∠OHA,
∴∠AOH=∠DCH=60°,
∴∠AOB=180°﹣∠AOH=120°.
一、选择题(每小题3分,共30分)
1.以下四个标志中,是轴对称图形的是(??? )
A.?????????????????B.?????????????????C.?????????????????D.?
2.下列图形中不是轴对称图形的是(?? )
A.??????????????????????????????B.?????????????????????????????C.??????????????????????????????D.?
3.如图,羊字象征吉祥和美满,如图的图案与羊有关,其中是轴对称的有( ?)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.等腰三角形的一条边长为5,另一边长为11,则它的底边长为(??? )
A.?5????????????????????????????????????????B.?11????????????????????????????????????????C.?6???????????????????????????????????????D.?5或11
5.如图,△ABC与△A′B′C′关于直线DE对称,且∠C=78°,∠B′=48°,则∠A的度数为(??? )
A.?48°???????????????????????????????????????B.?54°???????????????????????????????????????C.?74°???????????????????????????????????????D.?78°
6.如图, 周长为 ,把 的边 对折,使顶点 和点 重合,折痕交 边于点 ,交 边于点 ,连接 ,若 ,则 的周长是(?? )
A.??????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
7.等腰三角形的一个底角是 ,则它的顶角是( )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
8.如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是(?? )
A.?45°???????????????????????????????????????B.?60°???????????????????????????????????????C.?50°???????????????????????????????????????D.?55°
9.如图, 是 的角平分线, , , , 分别是垂足,若 , ,则 的长为(?? )
A.?3???????????????????????????????????????????B.?6???????????????????????????????????????????C.?9???????????????????????????????????????????D.?12
10.如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D,E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是(?? )
A.?到一个角两边距离相等的点在这个角的平分线上 B.?角平分线上的点到这个角两边的距离相等 C.?到线段两端点距离相等的点在这条线段的垂直平分线上 D.?线段垂直平分线上的点到线段两端点的距离相等
二、填空题(每小题3分,共18分)
11.已知一等腰三角形的两边长为3cm和7cm,则其腰长为________cm.
12.如图,在 中, , , , 与 的关系是________.
13.如图,在 中, 垂直平分 ,若 的周长是12, ,则 的长________.
14.如图,在Rt△ABC中,∠B =90°,ED是AC的垂直平分线,交AC于点D,交BC于E. 已知∠BAE=10°,则∠C的度数为________度.
15.如图,OP平分∠AOB,PB⊥OB,PB=2cm,则点P到OA的距离是________cm.
16.如图△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠EDF=________.
三、解答题(共8题;共52分)
17.如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
18.如图,在 中, ,M为BC的中点, 于点D, 于点 求证: .
19.如图1,已知三角形纸片ABC, , ,将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,求 的大小.
20.如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
21.如图,已知:AB=AD,BC=CD,AE⊥BC,垂足为E,AF⊥CD,垂足为F.
求证:
(1)∠B=∠D;
(2)AE=AF.
22.如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC=________°.
23.如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.
(1)画△ABC关于直线MN的对称图形△A1B1C1不写画法 ;
(2)求△AB的面积;
24.如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O.
(1)求证:△ACE≌△DCB;
(2)求∠AOB的度数.
2019-2020北师大版七年级数学下册第五章生活中的轴对称单元卷解析版
一、选择题
1.解:A、是中心对称图形,不是轴对称图形,不符合题意; B、既不是轴对称图形也不是中心对称图形,不符合题意; C、是轴对称图形,符合题意; D、既不是轴对称图形也不是中心对称图形,不符合题意. 故答案为:C. 2.观察图形可知B、C、D都是轴对称图形,
A不是轴对称图形.
故选A.
3.解:由图可得,第一个和第二个是轴对称图形,共2个.
故答案为:B.
4.解:若等腰三角形的底边为5,则两腰长为11,这时三角形三边关系满足 ,可以组成三角形,所以成立;
若等腰三角形的底边为11,则两腰长为5,这时三角形三边关系为 ,不能组成三角形,所以不成立;
所以等腰三角形底边为5,
故答案为:A.
5.解:∵△ABC与△A′B′C′关于直线DE对称, ∴∠B=∠B′=48° ∵在△ABC中,∠C=78°,∠B=∠B′=48°, ∴∠A=180°?78°?48°=54° 故答案为:B. 6.∵△ABC的边AC对折顶点C和点A重合,
∴AE=EC,AD=CD,
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC,
∵AE=6cm,
∴AC=AE+EC=6+6=12,
∵△ABC的周长为30cm,
∴AB+BC=30?12=18cm,
∴△ABD的周长是18cm.
故答案为:B.
7.解:∵一个等腰三角形的一个底角是40°,
∴另一个底角也是40°,
∴顶角为:180°-40°×2
=180°-80°
=100°
故答案为:C.
8.解:∵MN是AE的垂直平分线,
∴AC=EC,
∴∠CAE=∠E,
∴∠ACB=∠CAE+∠E=2∠E,
∵AB=CE,
∴AC=CE, ∴∠B=∠ACB=2∠E,
在△ABC中,∠BAE+∠B+∠E=180°,
∴105°+2∠E+∠E=180°
即∠E=25°.
∴∠B=2∠E=50°.
故答案为:C.
9.解:∵ ,
∴
∴
又∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴
即AC= .
故选:A.
10.∵OD=OE,
∴O点在线段DE的垂直平分线上,
∵CD=CE,
∴C点在线段DE的垂直平分线上,
∴CO是线段DE的垂直平分线上,
∴OC⊥l.
故选:C.
二、填空题
11.等腰三角形腰长相等,该等腰三角形的三边长分别为:3,3,7或3,7,7
∵三角形两边之和大于第三边
∴该等腰三角形的腰长为7
故答案为:7
12.解:∵AB=AC,
∴∠B=∠C,
∵BF=CD,BD=CE,
∴△BDF≌△CED(SAS),
∴∠BFD=∠EDC,
∵α+∠BDF+∠EDC=180°,
∴α+∠BDF+∠BFD=180°,
∵∠B+∠BDF+∠BFD=180°,
∴∠B=α,
∴∠C=∠B=α,
∵∠A+∠B+∠C=180°,
∴2α+∠A=180°,
∴ ,
故答案为: .
13.∵DE垂直平分AC,
∴AD=CD.
∵△BCD的周长是12,BC=4,
∴AB=BD+CD=12-4=8,
故答案为:8.
14.解:∵ ED是AC的垂直平分线, ∴EA=EC, ∴∠EAC=∠ECA, 设∠EAC=x, ∵∠EAC+∠ECA+∠BAE+∠ABC=180°, 即2x+10°+90°=180°, 解得x=40°. 故答案为:40. 15.解:过点P作PD⊥OA于点D,
∵OP平分∠AOB,PB⊥OB,PB=2cm,
∴PD=PB=2cm,
故答案为2.
16.∵AB=AC
∴∠B=∠C
∵FD⊥BC于D,DE⊥AB于E
∴∠BED=∠FDC=90°,
又∵∠B=∠C,
∴∠EDB=∠CFD
∵∠AFD=158°
∴∠EDB=∠CFD=180°-158°=22°
∴∠EDF=90°-∠EDB=90°-22°=68°
三、解答题
17. 解:∵△ABC是等边三角形,AD为中线,
∴AD⊥BC,∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED= =75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
18. 证明:连接AM,如图,
在 和 中
,
≌ ,???
,
, ,???
19. 解:? ∵AB=AC, ∴∠ABC=∠ACB,
而? ∠A=50°, ∴∠ABC=(180°-50°)=65°
∵?使点A与点B重合,折痕为ED, ∴∠ABD=∠A=50°,
∴∠DBC=∠ABC-∠ABD=65°-50°=15°.
20. 解:如图所示:
21. (1)证明:在△ABC与△ADC中,
,
∴△ABC≌△ADC,
∴∠B=∠D
(2)证明:∵△ABC≌△ADC,
∴∠ACB=∠ACD,
∵AE⊥BC,垂足为E,AF⊥CD,垂足为F,
∴AE=AF
22.(1)解:∵AB=AC,
∴∠B=∠ACF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS)
(2)75
解:(2)∵△ABE≌△ACF,∠BAE=30°,
∴∠CAF=∠BAE=30°,
∵AD=AC,
∴∠ADC=∠ACD,
∴∠ADC= =75°,
故答案为:75.
23.(1)解:如图所示
(2)解:S△ABC=4×5﹣ ×1×4﹣ ×1×4﹣ ×3×5=8.5
24. (1)解:如图:AC与BD交于点H.
∵△ACD,△BCE都是等边三角形,
∴CD=CA,CB=CE,∠ACD=∠BCE=60°,
∴∠DCB=∠ACE,
在△DCB和△ACE中,
,
∴△DCB≌△ACE(SAS),
(2)解:∵△DCB≌△ACE,
∴∠CAE=∠CDB,
∵∠DCH+∠CHD+∠BDC=180°,∠AOH+∠AHO+∠CAE=180°,∠DHC=∠OHA,
∴∠AOH=∠DCH=60°,
∴∠AOB=180°﹣∠AOH=120°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
