人教版八年级数学下册 17.1 勾股定理课件(4课时 共51张)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理课件(4课时 共51张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 15:24:53 | ||
图片预览










文档简介
(共51张PPT)
新课导入
目前世界上许多科学家正在试图寻找其他星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等。我国数学家华罗庚曾建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的。这个事实可以说明勾股定理的重大意义。尤其是在两千年前,是非常了不起的成就。
毕达哥拉斯头像
毕达哥拉斯(Pythagoras,572 BC?—497 BC?)古希腊数学家、哲学家。无论是解说外在物质世界,还是描写内在精神世界,都不能没有数学!最早悟出万事万物背后都有数的法则在起作用,是生活在2500年前的毕达哥拉斯。
毕达哥拉斯简介
毕达哥拉斯本人以发现勾股定理(西方称毕达哥拉斯定理)著称于世。这定理早已为巴比伦人和中国人所知(在中国古代大约是战国时期西汉的数学著作 《周髀 算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。这就是中国著名的勾股定理.),不过最早的证明大概可归功于毕达哥拉斯。他是用演绎法证明了直角三角形斜边平方等于两直角边平方之和,即毕达哥拉斯定理(勾股定理)。
毕达哥拉斯定理——勾股定理
17.1 勾股定理
了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
过程与方法
知识与能力
教学目标
培养在实际生活中发现问题总结规律的意识和能力。
介绍我国古代在勾股定理研究方面所取得的成就,激发爱国热情,促其勤奋学习。
情感态度与价值观
勾股定理的内容及证明。
勾股定理的证明。
重点
难点
教学重难点
我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五。”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5。让学生画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出AB的长。
你是否发现 与 的关系, 和 的关系? 对于任意的直角三角形也有这个性质吗?
猜想
命题1 如果直角 三角形的两直角边分别为a、b斜边长为c,那么
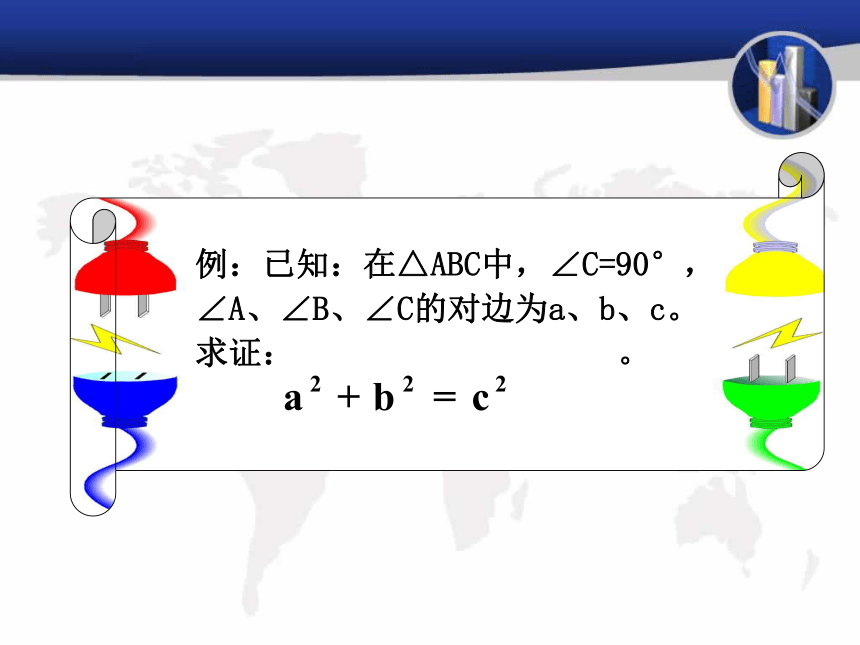
例:已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
求证: 。
勾股定理的证明方法,达300余种。你有那些方法证明呢?
赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四。以勾股之差相乘为中黄实。加差实,亦成弦实。
证明:如图所示,根据面积相等的原理有:
即:
知识要点
经过证明确认正确的命题叫做定理(theorem)。
命题1与直角三角形的边有关,我们把它称为勾股定理,即:如果直角三角形的两直角边分别为a,b斜边长为c,那么
1.勾股定理的内容。
如果直角三角形的两直角边分别为a,b,斜边长为c,那么
2.勾股定理的证明。
根据面积相等原理,四个直角三角形的面积加小正方形的面积等于大正方形的面积。
课堂小结
1.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
(1)两锐角之间的关系: ;
(2)若D为斜边中点,则斜边中线 ;
(3)若∠B=30°,则∠B的对边和斜边: ;
(4)三边之间的关系: 。
随堂练习
2.△ABC的三边a、b、c,
若满足 ,则 =90°;
若满足 ,则∠B是 角;
若满足 ,则∠B是 角。
∠B
钝
锐
17.1.2 勾股定理
树立数形结合的思想、分类讨论思想。
过程与方法
知识与能力
情感态度与价值观
教学目标
会用勾股定理进行简单的计算。
树立数形结合的思想、分类讨论思想。
勾股定理的简单计算。
勾股定理的灵活运用。
教学重难点
重点
难点
想一想
勾股定理的文字叙述;勾股定理的符号语言及变形。
勾股定理的文字叙述:如果直角三角形的两直角边分别为a,b,斜边长为c,那么 。
勾股定理的符号叙述:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c,则 。
勾股定理的变形:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c,则 , 。
知识要点
例:在Rt△ABC,∠C=90°
(1)已知a=b=5,求c。
(2)已知a=1,c=2,求b。
(3)已知c=17,b=8,求a。
(4)已知a:b=1:2,c=5,求a。
(5)已知b=15,∠A=30°,求a,c。
解:
勾股定理的简单计算。
课堂小结
1.填空:
(1)在Rt△ABC,∠C=90°,a=8,b=15,则c= 。
(2)在Rt△ABC,∠B=90°,a=3,b=4,则c= 。
(3)在Rt△ABC,∠C=90°,c=10,a:b=3:4,
则a= ,b= 。
(4)一个直角三角形的三边为三个连续偶数,
则它的三边长分别为 。
(5)已知直角三角形的两边长分别为3cm和5cm,
则第三边长为 。
(6)已知等边三角形的边长为2cm,
则它的高为 ,面积为 。
随堂练习
2.已知:如图,等边△ABC的边长是6cm。
(1)求等边△ABC的高。
(2)求S△ABC。
答案:(1)
(2)
3.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,AB⊥AC,∠B=60°,CD=1cm,
求BC的长。
解:BC=8cm
17.1.3勾股定理
树立数形结合的思想。
过程与方法
知识与能力
情感态度与价值观
教学目标
会用勾股定理解决简单的实际问题。
树立数形结合的思想。
勾股定理的应用。
实际问题向数学问题的转化。
教学重难点
教学重点
教学难点
勾股定理除了考试有用,在平时有什么用啊?
用处可多了!比如:农村房屋的屋顶构造,就可以用勾股定理来计算;设计工程图纸也要用到勾股定理等等。
也对,的确是哦!看来我得好好看看怎么用勾股定理,我以后要自己修一座属于自己的别墅!
哈哈…..
修别墅可不是简单的,但是这必定用到勾股定理,接下来就来看看我们是如何利用勾股定理解决问题的!
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
解:能通过。
探究1
如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子低端B也外移0.5m吗?
解:不是。
探究2
用勾股定理解决简单的实际问题。
课堂小结
1.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
随堂练习
2.如图,山坡上两株树木之间的坡面距离是4米,则这两株树之间的垂直距离是 米,水平距离是 米
3.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 米。
4.如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少?
17.1.4勾股定理
树立数形结合的思想。
过程与方法
知识与能力
情感态度与价值观
教学目标
会用勾股定理解决较综合的问题。
树立数形结合的思想。
勾股定理的综合应用。
勾股定理的综合应用。
重点
教学重难点
难点
勾股定理:如果直角三角形的两直角边分别为a,b,斜边长为c,那么 。
回顾旧知
例1:已知:在Rt △ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD= ,求线段AB的长。
解:
例2:已知:如图,△ABC中,AC=4,∠B=45°,∠A=60°,根据题设可知什么?
解:
例3:已知,如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。
解一般三角形的问题常常通过作高转化为直角三角形的问题。
归 纳
解:延长AD、BC交于E。
∵∠A=∠60°,∠B=90°,∴∠E=30°。
∴AE=2AB=8,CE=2CD=4,
∴
∴
∴
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
探究
不规则图形的面积,可转化为特殊图形求解。
归 纳
能,根据勾股
定理就可以得到。
1.△ABC中,∠C=90°,AB=4,BC= ,CD⊥AB于D,则AC= ,CD= ,BD= ,AD= ,S△ABC= 。
随堂练习
2.已知:如图,△ABC中,AB=26,BC=25,AC=17,求S△ABC。
勾股定理解决较综合的问题。
归 纳
新课导入
目前世界上许多科学家正在试图寻找其他星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等。我国数学家华罗庚曾建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的。这个事实可以说明勾股定理的重大意义。尤其是在两千年前,是非常了不起的成就。
毕达哥拉斯头像
毕达哥拉斯(Pythagoras,572 BC?—497 BC?)古希腊数学家、哲学家。无论是解说外在物质世界,还是描写内在精神世界,都不能没有数学!最早悟出万事万物背后都有数的法则在起作用,是生活在2500年前的毕达哥拉斯。
毕达哥拉斯简介
毕达哥拉斯本人以发现勾股定理(西方称毕达哥拉斯定理)著称于世。这定理早已为巴比伦人和中国人所知(在中国古代大约是战国时期西汉的数学著作 《周髀 算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。这就是中国著名的勾股定理.),不过最早的证明大概可归功于毕达哥拉斯。他是用演绎法证明了直角三角形斜边平方等于两直角边平方之和,即毕达哥拉斯定理(勾股定理)。
毕达哥拉斯定理——勾股定理
17.1 勾股定理
了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
过程与方法
知识与能力
教学目标
培养在实际生活中发现问题总结规律的意识和能力。
介绍我国古代在勾股定理研究方面所取得的成就,激发爱国热情,促其勤奋学习。
情感态度与价值观
勾股定理的内容及证明。
勾股定理的证明。
重点
难点
教学重难点
我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五。”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5。让学生画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出AB的长。
你是否发现 与 的关系, 和 的关系? 对于任意的直角三角形也有这个性质吗?
猜想
命题1 如果直角 三角形的两直角边分别为a、b斜边长为c,那么
例:已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
求证: 。
勾股定理的证明方法,达300余种。你有那些方法证明呢?
赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四。以勾股之差相乘为中黄实。加差实,亦成弦实。
证明:如图所示,根据面积相等的原理有:
即:
知识要点
经过证明确认正确的命题叫做定理(theorem)。
命题1与直角三角形的边有关,我们把它称为勾股定理,即:如果直角三角形的两直角边分别为a,b斜边长为c,那么
1.勾股定理的内容。
如果直角三角形的两直角边分别为a,b,斜边长为c,那么
2.勾股定理的证明。
根据面积相等原理,四个直角三角形的面积加小正方形的面积等于大正方形的面积。
课堂小结
1.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
(1)两锐角之间的关系: ;
(2)若D为斜边中点,则斜边中线 ;
(3)若∠B=30°,则∠B的对边和斜边: ;
(4)三边之间的关系: 。
随堂练习
2.△ABC的三边a、b、c,
若满足 ,则 =90°;
若满足 ,则∠B是 角;
若满足 ,则∠B是 角。
∠B
钝
锐
17.1.2 勾股定理
树立数形结合的思想、分类讨论思想。
过程与方法
知识与能力
情感态度与价值观
教学目标
会用勾股定理进行简单的计算。
树立数形结合的思想、分类讨论思想。
勾股定理的简单计算。
勾股定理的灵活运用。
教学重难点
重点
难点
想一想
勾股定理的文字叙述;勾股定理的符号语言及变形。
勾股定理的文字叙述:如果直角三角形的两直角边分别为a,b,斜边长为c,那么 。
勾股定理的符号叙述:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c,则 。
勾股定理的变形:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c,则 , 。
知识要点
例:在Rt△ABC,∠C=90°
(1)已知a=b=5,求c。
(2)已知a=1,c=2,求b。
(3)已知c=17,b=8,求a。
(4)已知a:b=1:2,c=5,求a。
(5)已知b=15,∠A=30°,求a,c。
解:
勾股定理的简单计算。
课堂小结
1.填空:
(1)在Rt△ABC,∠C=90°,a=8,b=15,则c= 。
(2)在Rt△ABC,∠B=90°,a=3,b=4,则c= 。
(3)在Rt△ABC,∠C=90°,c=10,a:b=3:4,
则a= ,b= 。
(4)一个直角三角形的三边为三个连续偶数,
则它的三边长分别为 。
(5)已知直角三角形的两边长分别为3cm和5cm,
则第三边长为 。
(6)已知等边三角形的边长为2cm,
则它的高为 ,面积为 。
随堂练习
2.已知:如图,等边△ABC的边长是6cm。
(1)求等边△ABC的高。
(2)求S△ABC。
答案:(1)
(2)
3.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,AB⊥AC,∠B=60°,CD=1cm,
求BC的长。
解:BC=8cm
17.1.3勾股定理
树立数形结合的思想。
过程与方法
知识与能力
情感态度与价值观
教学目标
会用勾股定理解决简单的实际问题。
树立数形结合的思想。
勾股定理的应用。
实际问题向数学问题的转化。
教学重难点
教学重点
教学难点
勾股定理除了考试有用,在平时有什么用啊?
用处可多了!比如:农村房屋的屋顶构造,就可以用勾股定理来计算;设计工程图纸也要用到勾股定理等等。
也对,的确是哦!看来我得好好看看怎么用勾股定理,我以后要自己修一座属于自己的别墅!
哈哈…..
修别墅可不是简单的,但是这必定用到勾股定理,接下来就来看看我们是如何利用勾股定理解决问题的!
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
解:能通过。
探究1
如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子低端B也外移0.5m吗?
解:不是。
探究2
用勾股定理解决简单的实际问题。
课堂小结
1.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
随堂练习
2.如图,山坡上两株树木之间的坡面距离是4米,则这两株树之间的垂直距离是 米,水平距离是 米
3.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 米。
4.如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少?
17.1.4勾股定理
树立数形结合的思想。
过程与方法
知识与能力
情感态度与价值观
教学目标
会用勾股定理解决较综合的问题。
树立数形结合的思想。
勾股定理的综合应用。
勾股定理的综合应用。
重点
教学重难点
难点
勾股定理:如果直角三角形的两直角边分别为a,b,斜边长为c,那么 。
回顾旧知
例1:已知:在Rt △ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD= ,求线段AB的长。
解:
例2:已知:如图,△ABC中,AC=4,∠B=45°,∠A=60°,根据题设可知什么?
解:
例3:已知,如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。
解一般三角形的问题常常通过作高转化为直角三角形的问题。
归 纳
解:延长AD、BC交于E。
∵∠A=∠60°,∠B=90°,∴∠E=30°。
∴AE=2AB=8,CE=2CD=4,
∴
∴
∴
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
探究
不规则图形的面积,可转化为特殊图形求解。
归 纳
能,根据勾股
定理就可以得到。
1.△ABC中,∠C=90°,AB=4,BC= ,CD⊥AB于D,则AC= ,CD= ,BD= ,AD= ,S△ABC= 。
随堂练习
2.已知:如图,△ABC中,AB=26,BC=25,AC=17,求S△ABC。
勾股定理解决较综合的问题。
归 纳
