人教版七年级数学下册 5.2.2平行线的判定课件(共30张PPT)
文档属性
| 名称 | 人教版七年级数学下册 5.2.2平行线的判定课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 701.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 17:34:55 | ||
图片预览






文档简介
(共30张PPT)
复习:
1.直线的位置关系有哪几种?
2.怎样的两条直线平行?
3.你知道平行线有哪些性质?
新课导入
知识与能力
1.掌握平行线的判定公理及推论;
2.会用数学语言表示平行线判定公理及其推论,并能根据它们做简单的推理证明.
教学目标
过程与方法
1.通过观察、思考探索等活动归纳出三种判定方法,培养转化的数学思想,培养动手、分析、解决实际问题的能力;
2.通过活动及实际问题的研究学会从数学角度发现和提出问题,并用数学方法探索、研究和解决问题.
教学目标
情感态度与价值观
1.感受数学与生活的紧密联系,体会数学的价值,激发学习数学的兴趣,培养敢想、敢说、敢解决实际问题的学习习惯;
? 2.通过体验、猜想并证明,体会数学充满着探索和创造,培养团结协作,勇于创新的精神;
3.通过“转化”数学思想方法的运用,认识事物之间是普遍联系,相互转化的辩证唯物主义思想.
教学目标
重点
难点
平行线的判定方法.
“转化”的数学思想的培养,综合运用三个平行线的判定方法.
教学重难点
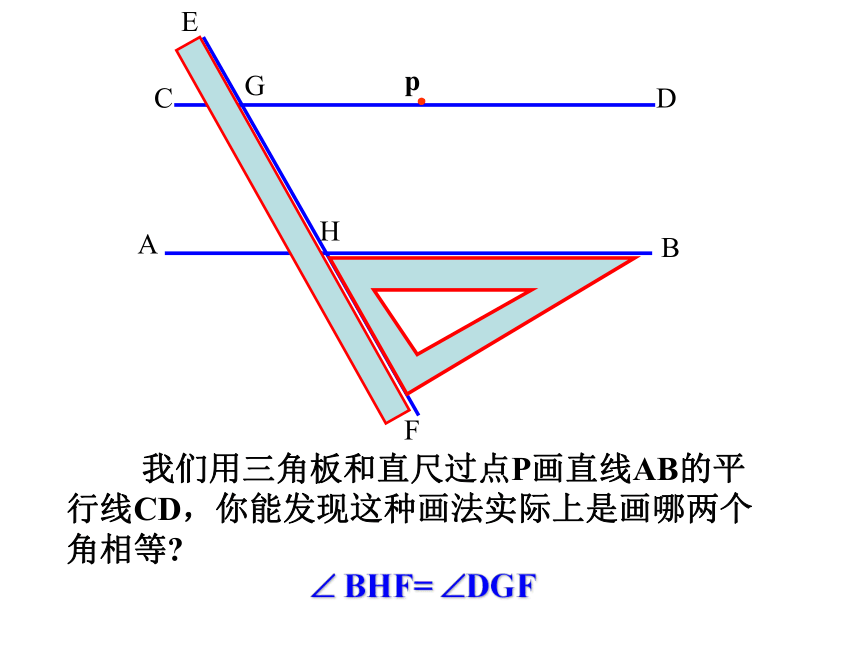
? BHF= ?DGF
C
D
A
B
E
F
G
H
.
p
我们用三角板和直尺过点P画直线AB的平行线CD,你能发现这种画法实际上是画哪两个角相等?
H
G
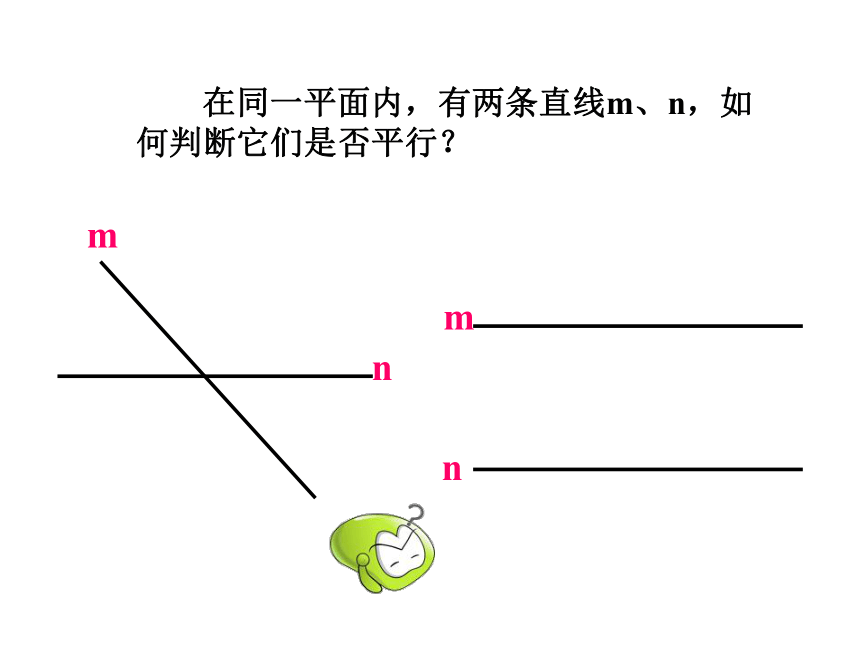
在同一平面内,有两条直线m、n,如何判断它们是否平行?
m
n
m
n
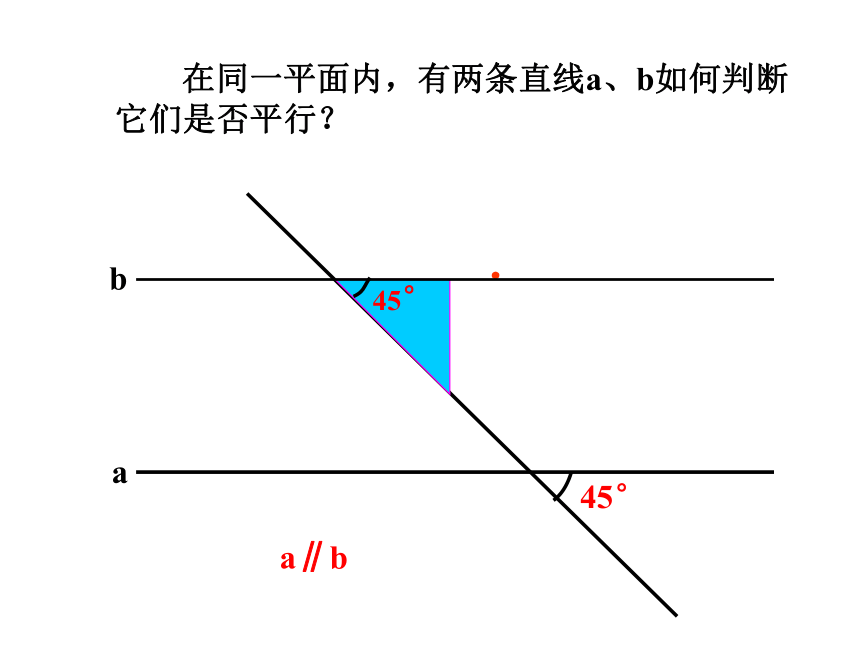
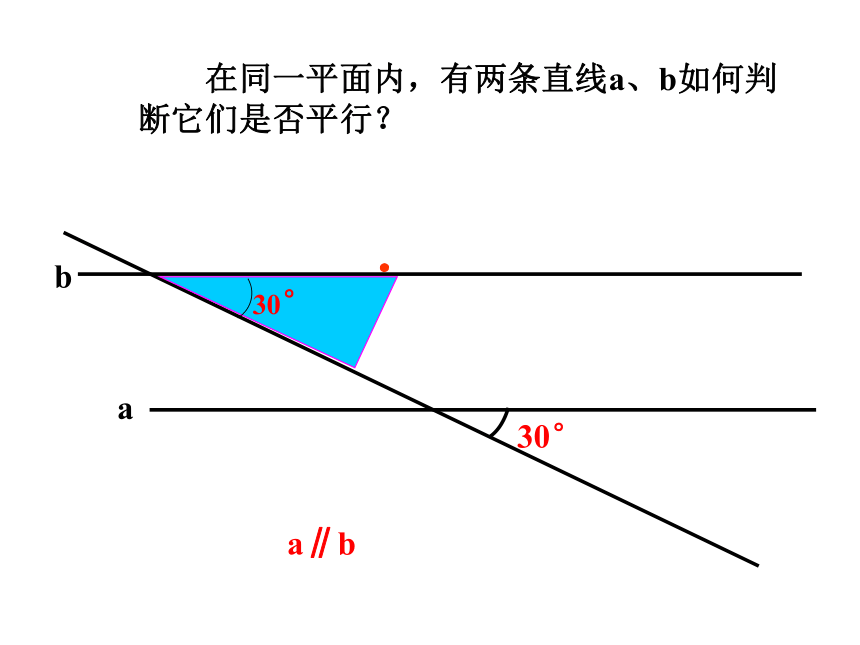
在同一平面内,有两条直线a、b如何判断
它们是否平行?
45°
.
45°
a
b
a∥b
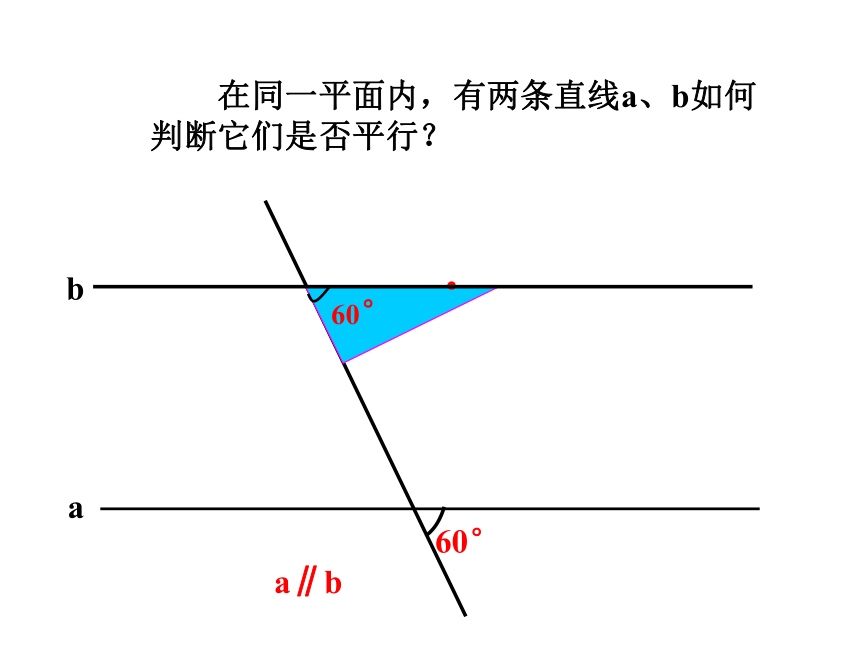
60°
在同一平面内,有两条直线a、b如何判断它们是否平行?
●
60°
a
b
a∥b
在同一平面内,有两条直线a、b如何判断它们是否平行?
30°
.
30°
a
b
a∥b
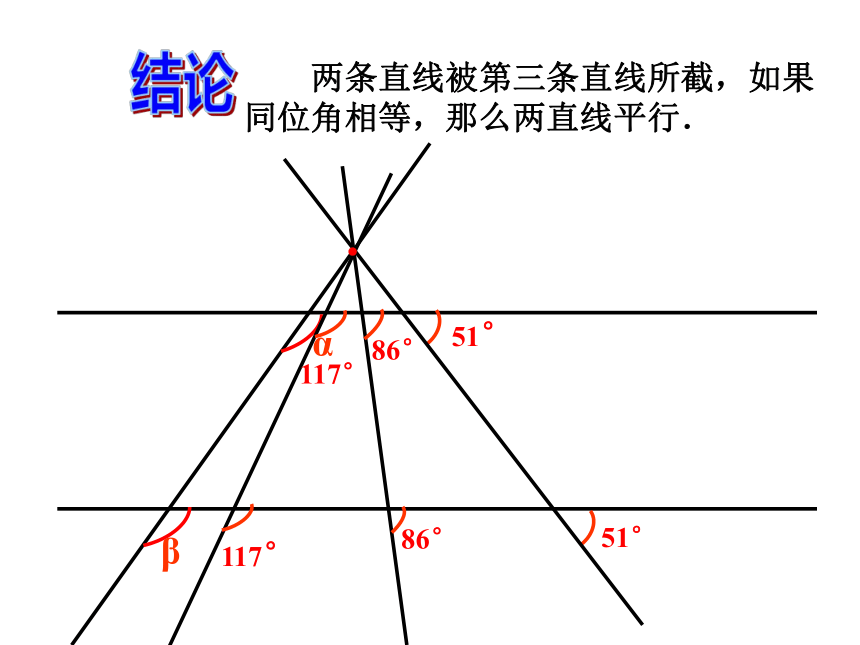
51°
51°
α
β
117°
117°
86°
86°
●
两条直线被第三条直线所截,如果同位角相等,那么两直线平行.
结论
126°
135°
126°
107°
141°
168°
72°
“会不会有某一特定时刻,即使同位角不等而两直线平行呢?”
两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行.
简单说成:
同位角相等、两直线平行
α
β
a
b
c
知识要点
平行线的判定方法1:
同位角相等两直线平行.
即:
因为? DHF= ? BGF,
所以AB ∥CD.
A
B
C
D
E
F
G
H
EF∥GH
∠2 =∠5
EF∥GH
∠3 =∠4
如果 , 能判定哪两条直线平行?
∠1 =∠2
AB∥CD
4
1
2
3
A
B
C
E
F
D
5
H
G
如图,哪两个角相等能判定直线AB∥CD?
∠3=∠4
1
4
3
2
A
D
C
B
装修工人正在向墙上钉木条,如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行?
90°
a
b
如下图,木工用角尺的一边紧靠工件边缘,另一边画条直线a,b.这两条直线平行吗?为什么?
直线a与b平行.
同位角相等,两直线平行.
能否利用内错角和同旁内角来判定两直线平行呢?
想一想
解: 因为?2=?3(已知)
且?1=?2(对顶角相等)
所以?1= ?3
所以m//n(同位角相等,两直线平行).
如果?2= ?3,m//n?写出你的推导过程.
n
m
l
2
3
1
两条直线被第三条直线所截,如果内错角相等,那么两条直线平行.
简单说成:内错角相等,两直线平行.
知识要点
平行线的判定方法2:
如果?1+?2=1800 能判定m//n吗?写出你的推导过程.
解: 因为?1+?2=180°
?2+?3=180°
所以?1=?3
所以 m//n(同位角相等,两直线平行) .
3
1
2
m
n
l
两条直线被第三条直线所截,如果同旁内角相等,那么两条直线平行.
简单说成:同旁内角互补,两直线平行.
知识要点
平行线的判定方法3:
例:已知:如图,∠1=∠4,∠2=∠3,求证: l1∥l2.
解:因为∠1=∠4,
∠3=∠4(对顶角相等),
所以∠1=∠3,
所以 l1∥l3(同位角相等,两直线平行)
因为∠2=∠3(内错角相等,两直线平行),
所以l2∥l3,
所以l1∥l2.
图形
条件
结论
理由
同位角
内错角
同旁内角
a//b
a//b
a//b
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
平行线的判定
课堂小结
∠1=∠2
∠2=∠3
∠2+∠4=180°
1
2
)
)
a
b
c
2
3
)
)
a
b
c
2
4
)
)
a
b
c
解: 因为 ∠1=82°, ∠2=98° (已知)
所以∠1+∠2= ( )
又因为 +∠5=180°( )
所以 ∠1=∠5 ( )
所以 a//b ( )
所以 =∠4 ( )
又因为 ∠3=80°(已知)
所以 ( )
a
b
c
d
1
5
2
4
3
180°
等式性质
∠2
邻补角的定义
同角的补角相等
同位角相等,两直线平行
∠3
两直线平行,内错角相等
∠4=80°
等量代换
随堂练习
1.如图,∠1=82°, ∠2=98°,∠3=80°,求∠4的度数.
解: 因为 AD//BC ( 已知 )
所以∠CAD=∠C ( )
∠BAD+∠B=180° ( )
又因为∠B=50° ( 已知)
所以∠BAD = ( )
因为 (已知)
所以∠ = ∠BAD ( )
所以∠ CAD =_____
所以 ( )
A
B
C
D
两直线平行,内错角相等
两直线平行,同旁内角互补
130°
等式性质
AC平分∠BAD
CAD
角平分线的定义
65°
∠C=65°
等量代换
2. 如图,已知:AD//BC,AC平分∠BAD,∠ B=50°,求∠C的度数.
3.如图:
若? 1= ? 3可以判断哪两条直线平行?
若? 2= ? 4可以判断PM∥QN吗?为什么?
提示: 由? 1= ? 3,可以判断PM∥QN;
因为? 1= ? 3,
? 2= ? 4,
所以(∠1+∠2)=(∠3+∠4),
所以∠BPE=∠EQD,
所以 PM ∥ QN(同位角相等,两直线平行).
复习:
1.直线的位置关系有哪几种?
2.怎样的两条直线平行?
3.你知道平行线有哪些性质?
新课导入
知识与能力
1.掌握平行线的判定公理及推论;
2.会用数学语言表示平行线判定公理及其推论,并能根据它们做简单的推理证明.
教学目标
过程与方法
1.通过观察、思考探索等活动归纳出三种判定方法,培养转化的数学思想,培养动手、分析、解决实际问题的能力;
2.通过活动及实际问题的研究学会从数学角度发现和提出问题,并用数学方法探索、研究和解决问题.
教学目标
情感态度与价值观
1.感受数学与生活的紧密联系,体会数学的价值,激发学习数学的兴趣,培养敢想、敢说、敢解决实际问题的学习习惯;
? 2.通过体验、猜想并证明,体会数学充满着探索和创造,培养团结协作,勇于创新的精神;
3.通过“转化”数学思想方法的运用,认识事物之间是普遍联系,相互转化的辩证唯物主义思想.
教学目标
重点
难点
平行线的判定方法.
“转化”的数学思想的培养,综合运用三个平行线的判定方法.
教学重难点
? BHF= ?DGF
C
D
A
B
E
F
G
H
.
p
我们用三角板和直尺过点P画直线AB的平行线CD,你能发现这种画法实际上是画哪两个角相等?
H
G
在同一平面内,有两条直线m、n,如何判断它们是否平行?
m
n
m
n
在同一平面内,有两条直线a、b如何判断
它们是否平行?
45°
.
45°
a
b
a∥b
60°
在同一平面内,有两条直线a、b如何判断它们是否平行?
●
60°
a
b
a∥b
在同一平面内,有两条直线a、b如何判断它们是否平行?
30°
.
30°
a
b
a∥b
51°
51°
α
β
117°
117°
86°
86°
●
两条直线被第三条直线所截,如果同位角相等,那么两直线平行.
结论
126°
135°
126°
107°
141°
168°
72°
“会不会有某一特定时刻,即使同位角不等而两直线平行呢?”
两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行.
简单说成:
同位角相等、两直线平行
α
β
a
b
c
知识要点
平行线的判定方法1:
同位角相等两直线平行.
即:
因为? DHF= ? BGF,
所以AB ∥CD.
A
B
C
D
E
F
G
H
EF∥GH
∠2 =∠5
EF∥GH
∠3 =∠4
如果 , 能判定哪两条直线平行?
∠1 =∠2
AB∥CD
4
1
2
3
A
B
C
E
F
D
5
H
G
如图,哪两个角相等能判定直线AB∥CD?
∠3=∠4
1
4
3
2
A
D
C
B
装修工人正在向墙上钉木条,如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行?
90°
a
b
如下图,木工用角尺的一边紧靠工件边缘,另一边画条直线a,b.这两条直线平行吗?为什么?
直线a与b平行.
同位角相等,两直线平行.
能否利用内错角和同旁内角来判定两直线平行呢?
想一想
解: 因为?2=?3(已知)
且?1=?2(对顶角相等)
所以?1= ?3
所以m//n(同位角相等,两直线平行).
如果?2= ?3,m//n?写出你的推导过程.
n
m
l
2
3
1
两条直线被第三条直线所截,如果内错角相等,那么两条直线平行.
简单说成:内错角相等,两直线平行.
知识要点
平行线的判定方法2:
如果?1+?2=1800 能判定m//n吗?写出你的推导过程.
解: 因为?1+?2=180°
?2+?3=180°
所以?1=?3
所以 m//n(同位角相等,两直线平行) .
3
1
2
m
n
l
两条直线被第三条直线所截,如果同旁内角相等,那么两条直线平行.
简单说成:同旁内角互补,两直线平行.
知识要点
平行线的判定方法3:
例:已知:如图,∠1=∠4,∠2=∠3,求证: l1∥l2.
解:因为∠1=∠4,
∠3=∠4(对顶角相等),
所以∠1=∠3,
所以 l1∥l3(同位角相等,两直线平行)
因为∠2=∠3(内错角相等,两直线平行),
所以l2∥l3,
所以l1∥l2.
图形
条件
结论
理由
同位角
内错角
同旁内角
a//b
a//b
a//b
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
平行线的判定
课堂小结
∠1=∠2
∠2=∠3
∠2+∠4=180°
1
2
)
)
a
b
c
2
3
)
)
a
b
c
2
4
)
)
a
b
c
解: 因为 ∠1=82°, ∠2=98° (已知)
所以∠1+∠2= ( )
又因为 +∠5=180°( )
所以 ∠1=∠5 ( )
所以 a//b ( )
所以 =∠4 ( )
又因为 ∠3=80°(已知)
所以 ( )
a
b
c
d
1
5
2
4
3
180°
等式性质
∠2
邻补角的定义
同角的补角相等
同位角相等,两直线平行
∠3
两直线平行,内错角相等
∠4=80°
等量代换
随堂练习
1.如图,∠1=82°, ∠2=98°,∠3=80°,求∠4的度数.
解: 因为 AD//BC ( 已知 )
所以∠CAD=∠C ( )
∠BAD+∠B=180° ( )
又因为∠B=50° ( 已知)
所以∠BAD = ( )
因为 (已知)
所以∠ = ∠BAD ( )
所以∠ CAD =_____
所以 ( )
A
B
C
D
两直线平行,内错角相等
两直线平行,同旁内角互补
130°
等式性质
AC平分∠BAD
CAD
角平分线的定义
65°
∠C=65°
等量代换
2. 如图,已知:AD//BC,AC平分∠BAD,∠ B=50°,求∠C的度数.
3.如图:
若? 1= ? 3可以判断哪两条直线平行?
若? 2= ? 4可以判断PM∥QN吗?为什么?
提示: 由? 1= ? 3,可以判断PM∥QN;
因为? 1= ? 3,
? 2= ? 4,
所以(∠1+∠2)=(∠3+∠4),
所以∠BPE=∠EQD,
所以 PM ∥ QN(同位角相等,两直线平行).
