2019-2020学年高一数学人教A版必修1学案:3.2.1几类不同增长的函数模型Word版含答案
文档属性
| 名称 | 2019-2020学年高一数学人教A版必修1学案:3.2.1几类不同增长的函数模型Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 81.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-30 10:07:01 | ||
图片预览


文档简介
第三章 函数的应用
3.2 函数模型及其应用
3.2.1 几类不同增长的函数模型
学习目标
①结合实例体会直线上升、指数爆炸、对数增长等不同增长的函数模型意义,理解它们的增长差异性;
②能够借助信息技术,利用函数图象及数据表格,对几种常见增长类型的函数的增长状况进行比较,初步体会它们的增长差异性;收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数等),了解函数模型的广泛应用;
③体验函数是描述宏观世界变化规律的基本数学模型,体验指数函数、对数函数等函数与现实世界的密切联系及其在刻画现实问题中的作用.培养学生学数学、用数学、完善数学的正确的数学意识.
合作学习
一、设计问题,创设情境
问题1:猪八戒开招聘会,引出招聘的试题:猪氏集团旗下的“天鹏大酒店”已于2013年元旦开张,生意蒸蒸日上.第一个月营业额达到100万,第二个月达到了150万,第三个月为200万元.
试问:照此增长,第四个月的营业额为多少?
二、自主探索,尝试解决
由前面的问题情境,设置如下问题,学生小组讨论解决,各个小组之间互相交流.
问题2:进入高中以来,我们所学的函数中,哪些符合在x∈N*上单调递增?
问题3:上述猪八戒的营业额函数模型是否满足过点(1,1),(1,1.5)?
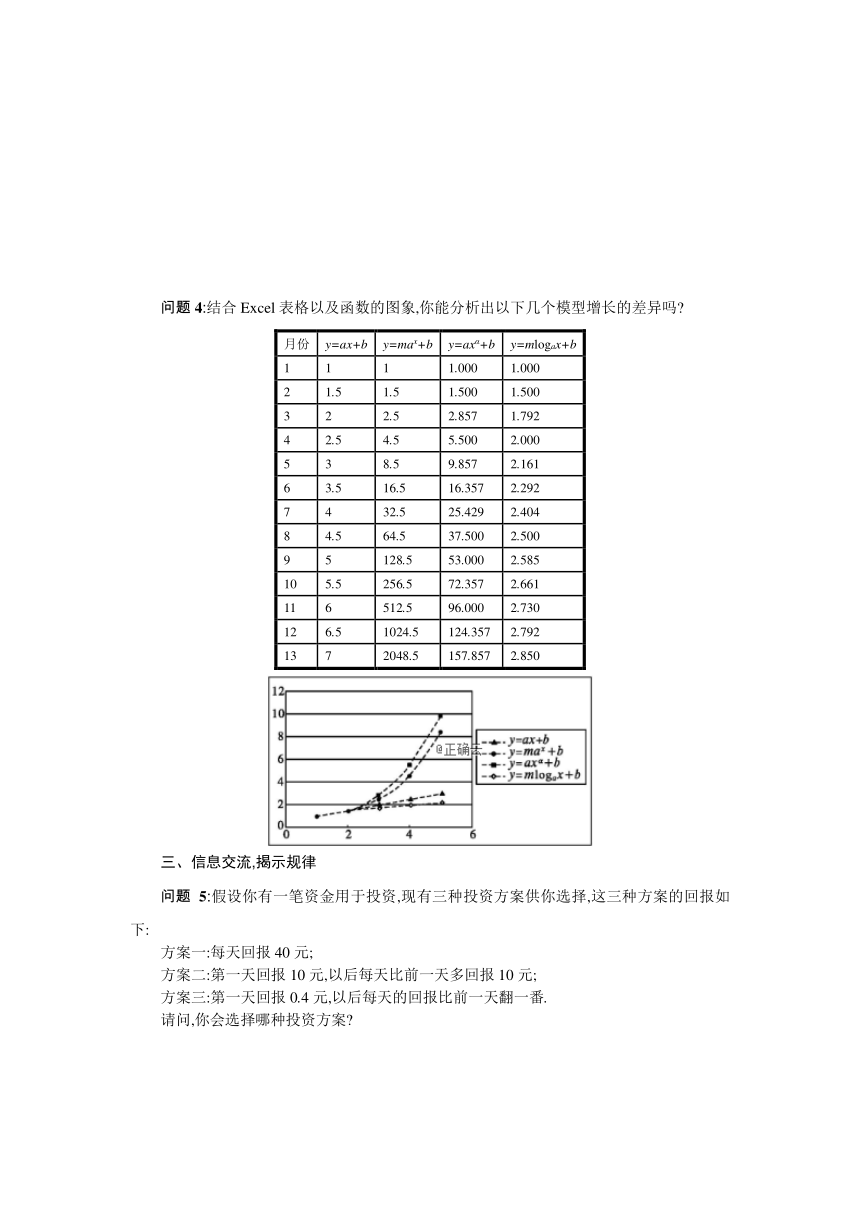
问题4:结合Excel表格以及函数的图象,你能分析出以下几个模型增长的差异吗?
月份
y=ax+b
y=max+b
y=axα+b
y=mlogax+b
1
1
1
1.000
1.000
2
1.5
1.5
1.500
1.500
3
2
2.5
2.857
1.792
4
2.5
4.5
5.500
2.000
5
3
8.5
9.857
2.161
6
3.5
16.5
16.357
2.292
7
4
32.5
25.429
2.404
8
4.5
64.5
37.500
2.500
9
5
128.5
53.000
2.585
10
5.5
256.5
72.357
2.661
11
6
512.5
96.000
2.730
12
6.5
1024.5
124.357
2.792
13
7
2048.5
157.857
2.850
三、信息交流,揭示规律
问题5:假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
针对上例可以思考下面问题:
①选择哪种方案是依据一天的回报数还是累计回报数?
②课本把两种回报数都列表给出的意义何在?
③由此得出怎样的结论?
四、运用规律,解决问题
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求?
五、课后作业
1.某种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个,…,现有2个这样的细胞,分裂x次后得到的细胞个数y为( )
A.y=2x+1 B.y=2x-1
C.y=2x D.y=2x
2.某公司为了适应市场需求对产品结构作了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
3.一等腰三角形的周长是20,底边长y是关于腰长x的函数,它的解析式为( )
A.y=20-2x (x≤10)
B.y=20-2x (x<10)
C.y=20-2x (5≤x≤10)
D.y=20-2x(54.某新品电视投放市场后第1个月销售100台,第2个月销售200台,第3个月销售400台,第4个月销售790台.则销量y与投放市场的月数x之间的关系可写成 .?
5.某种计算机病毒是通过电子邮件进行传播的,如果某台计算机感染上这种病毒,那么每轮病毒发作时,这台计算机都可能感染没被感染的20台计算机. 现有10台计算机在第1轮病毒发作时被感染,问在第5轮病毒发作时可能有 台计算机被感染. (用式子表示)?
参考答案
问题1:250万
问题2:一次函数,指数函数,对数函数.
问题3:满足.
问题4:略
三、信息交流,揭示规律
问题5:解:设第x天所得回报是y元,则方案一可以用函数y=40(x∈N*)进行描述;方案二可以用函数y=10x(x∈N*)进行描述;方案三可以用函数y=0.4×2x-1(x∈N*)进行描述.三个模型中,第一个是常数函数,后两个都是递增函数模型.要对三个方案作出选择,就要对它的增长情况进行分析.
我们先用计算器或计算机计算一下三种方案所得回报的增长情况:
x/天
方案一
方案二
方案三
y/元
增加量/元
y/元
增加量/元
y/元
增加量/元
1
40
10
0.4
2
40
0
20
10
0.8
0.4
3
40
0
30
10
1.6
0.8
4
40
0
40
10
3.2
1.6
5
40
0
50
10
6.4
3.2
6
40
0
60
10
12.8
6.4
7
40
0
70
10
25.6
12.8
8
40
0
80
10
51.2
25.6
9
40
0
90
10
102.4
51.2
10
40
0
100
10
204.8
102.4
…
…
…
…
…
…
…
30
40
0
300
10
214748364.8
107374182.4
再作出三个函数的图象.
由表和图可知,方案一的函数是常数函数,方案二、方案三的函数都是增函数,但方案三的函数与方案二的函数的增长情况很不相同.可以看到,尽管方案一、方案二在第1天所得回报分别是方案三的100倍和25倍,但它们的增长量固定不变,而方案三是“指数增长”,其“增长量”是成倍增加的,从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一、方案二所无法企及的.从每天所得回报看,在第1~3天,方案一最多;在第4天,方案一和方案二一样多,方案三最少;在第5~8天,方案二最多;第9天开始,方案三比其他两个方案所得回报多得多,到第30天,所得回报已超过2亿元.
下面再看累计的回报数.通过计算器或计算机列表如下.
天数回报//元方案
1
2
3
4
5
6
7
8
9
10
11
一
40
80
120
160
200
240
280
320
360
400
440
二
10
30
60
100
150
210
280
360
450
550
660
三
0.4
1.2
2.8
6
12.4
25.2
50.8
102
204.4
409.2
818.8
因此,投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8~10天,应选择方案二;投资11天(含11天)以上,则应选择方案三.
答案:①选择哪种方案依据的是累计回报数.
②让我们体会每天回报数的增长变化.
③上述例子只是一种假想情况,但从中我们可以体会到,不同的函数增长模型其增长变化存在很大差异.
四、运用规律,解决问题
解:借助计算器或计算机作出函数y=5,y=0.25x,y=log7x+1,y=1.002x的图象(如图).
观察函数的图象,在区间[10,1000]上,模型y=0.25x,y=1.002x的图象都有一部分在直线y=5的上方,只有模型y=log7x+1的图象始终在y=5的下方,这说明只有按模型y=log7x+1进行奖励时才符合公司的要求.
下面通过计算确认上述判断.
首先计算哪个模型的奖金总数不超过5万.
对于模型y=0.25x,它在区间[10,1000]上递增,而且当x=20时,y=5,因此,当x>20时,y>5,所以该模型不符合要求;
对于模型y=1.002x,由函数图象,并利用计算器,可知在区间(805,806)内有一个点x0满足1.00=5,由于它在区间[10,1000]上递增,因此当x>x0时,y>5,所以该模型也不符合要求;
对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,y=log71000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.
再计算按模型y=log7x+1奖励时,奖金是否不超过利润的25%,即当x∈[10,1000]时,是否有≤0.25成立.
令f(x)=log7x+1-0.25x,x∈[10,1000].利用计算器或计算机作出函数f(x)的图象(如图),由函数图象可知它是递减的,因此
f(x)≤f(10)≈-0.3167<0,即log7x+1<0.25x.
所以,当x∈[10,1000]时,<0.25.
说明按模型y=log7x+1奖励,奖金不超过利润的25%.
综上所述,模型y=log7x+1确实能符合公司的要求.
五、课后作业
1.A 2.D 3.D 4.y=100×2n-1 5.10×204
3.2 函数模型及其应用
3.2.1 几类不同增长的函数模型
学习目标
①结合实例体会直线上升、指数爆炸、对数增长等不同增长的函数模型意义,理解它们的增长差异性;
②能够借助信息技术,利用函数图象及数据表格,对几种常见增长类型的函数的增长状况进行比较,初步体会它们的增长差异性;收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数等),了解函数模型的广泛应用;
③体验函数是描述宏观世界变化规律的基本数学模型,体验指数函数、对数函数等函数与现实世界的密切联系及其在刻画现实问题中的作用.培养学生学数学、用数学、完善数学的正确的数学意识.
合作学习
一、设计问题,创设情境
问题1:猪八戒开招聘会,引出招聘的试题:猪氏集团旗下的“天鹏大酒店”已于2013年元旦开张,生意蒸蒸日上.第一个月营业额达到100万,第二个月达到了150万,第三个月为200万元.
试问:照此增长,第四个月的营业额为多少?
二、自主探索,尝试解决
由前面的问题情境,设置如下问题,学生小组讨论解决,各个小组之间互相交流.
问题2:进入高中以来,我们所学的函数中,哪些符合在x∈N*上单调递增?
问题3:上述猪八戒的营业额函数模型是否满足过点(1,1),(1,1.5)?
问题4:结合Excel表格以及函数的图象,你能分析出以下几个模型增长的差异吗?
月份
y=ax+b
y=max+b
y=axα+b
y=mlogax+b
1
1
1
1.000
1.000
2
1.5
1.5
1.500
1.500
3
2
2.5
2.857
1.792
4
2.5
4.5
5.500
2.000
5
3
8.5
9.857
2.161
6
3.5
16.5
16.357
2.292
7
4
32.5
25.429
2.404
8
4.5
64.5
37.500
2.500
9
5
128.5
53.000
2.585
10
5.5
256.5
72.357
2.661
11
6
512.5
96.000
2.730
12
6.5
1024.5
124.357
2.792
13
7
2048.5
157.857
2.850
三、信息交流,揭示规律
问题5:假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
针对上例可以思考下面问题:
①选择哪种方案是依据一天的回报数还是累计回报数?
②课本把两种回报数都列表给出的意义何在?
③由此得出怎样的结论?
四、运用规律,解决问题
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求?
五、课后作业
1.某种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个,…,现有2个这样的细胞,分裂x次后得到的细胞个数y为( )
A.y=2x+1 B.y=2x-1
C.y=2x D.y=2x
2.某公司为了适应市场需求对产品结构作了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
3.一等腰三角形的周长是20,底边长y是关于腰长x的函数,它的解析式为( )
A.y=20-2x (x≤10)
B.y=20-2x (x<10)
C.y=20-2x (5≤x≤10)
D.y=20-2x(5
5.某种计算机病毒是通过电子邮件进行传播的,如果某台计算机感染上这种病毒,那么每轮病毒发作时,这台计算机都可能感染没被感染的20台计算机. 现有10台计算机在第1轮病毒发作时被感染,问在第5轮病毒发作时可能有 台计算机被感染. (用式子表示)?
参考答案
问题1:250万
问题2:一次函数,指数函数,对数函数.
问题3:满足.
问题4:略
三、信息交流,揭示规律
问题5:解:设第x天所得回报是y元,则方案一可以用函数y=40(x∈N*)进行描述;方案二可以用函数y=10x(x∈N*)进行描述;方案三可以用函数y=0.4×2x-1(x∈N*)进行描述.三个模型中,第一个是常数函数,后两个都是递增函数模型.要对三个方案作出选择,就要对它的增长情况进行分析.
我们先用计算器或计算机计算一下三种方案所得回报的增长情况:
x/天
方案一
方案二
方案三
y/元
增加量/元
y/元
增加量/元
y/元
增加量/元
1
40
10
0.4
2
40
0
20
10
0.8
0.4
3
40
0
30
10
1.6
0.8
4
40
0
40
10
3.2
1.6
5
40
0
50
10
6.4
3.2
6
40
0
60
10
12.8
6.4
7
40
0
70
10
25.6
12.8
8
40
0
80
10
51.2
25.6
9
40
0
90
10
102.4
51.2
10
40
0
100
10
204.8
102.4
…
…
…
…
…
…
…
30
40
0
300
10
214748364.8
107374182.4
再作出三个函数的图象.
由表和图可知,方案一的函数是常数函数,方案二、方案三的函数都是增函数,但方案三的函数与方案二的函数的增长情况很不相同.可以看到,尽管方案一、方案二在第1天所得回报分别是方案三的100倍和25倍,但它们的增长量固定不变,而方案三是“指数增长”,其“增长量”是成倍增加的,从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一、方案二所无法企及的.从每天所得回报看,在第1~3天,方案一最多;在第4天,方案一和方案二一样多,方案三最少;在第5~8天,方案二最多;第9天开始,方案三比其他两个方案所得回报多得多,到第30天,所得回报已超过2亿元.
下面再看累计的回报数.通过计算器或计算机列表如下.
天数回报//元方案
1
2
3
4
5
6
7
8
9
10
11
一
40
80
120
160
200
240
280
320
360
400
440
二
10
30
60
100
150
210
280
360
450
550
660
三
0.4
1.2
2.8
6
12.4
25.2
50.8
102
204.4
409.2
818.8
因此,投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8~10天,应选择方案二;投资11天(含11天)以上,则应选择方案三.
答案:①选择哪种方案依据的是累计回报数.
②让我们体会每天回报数的增长变化.
③上述例子只是一种假想情况,但从中我们可以体会到,不同的函数增长模型其增长变化存在很大差异.
四、运用规律,解决问题
解:借助计算器或计算机作出函数y=5,y=0.25x,y=log7x+1,y=1.002x的图象(如图).
观察函数的图象,在区间[10,1000]上,模型y=0.25x,y=1.002x的图象都有一部分在直线y=5的上方,只有模型y=log7x+1的图象始终在y=5的下方,这说明只有按模型y=log7x+1进行奖励时才符合公司的要求.
下面通过计算确认上述判断.
首先计算哪个模型的奖金总数不超过5万.
对于模型y=0.25x,它在区间[10,1000]上递增,而且当x=20时,y=5,因此,当x>20时,y>5,所以该模型不符合要求;
对于模型y=1.002x,由函数图象,并利用计算器,可知在区间(805,806)内有一个点x0满足1.00=5,由于它在区间[10,1000]上递增,因此当x>x0时,y>5,所以该模型也不符合要求;
对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,y=log71000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.
再计算按模型y=log7x+1奖励时,奖金是否不超过利润的25%,即当x∈[10,1000]时,是否有≤0.25成立.
令f(x)=log7x+1-0.25x,x∈[10,1000].利用计算器或计算机作出函数f(x)的图象(如图),由函数图象可知它是递减的,因此
f(x)≤f(10)≈-0.3167<0,即log7x+1<0.25x.
所以,当x∈[10,1000]时,<0.25.
说明按模型y=log7x+1奖励,奖金不超过利润的25%.
综上所述,模型y=log7x+1确实能符合公司的要求.
五、课后作业
1.A 2.D 3.D 4.y=100×2n-1 5.10×204
