2019-2020学年高一数学人教A版必修1学案:第二章基本初等函数(Ⅰ)本章复习Word版含答案
文档属性
| 名称 | 2019-2020学年高一数学人教A版必修1学案:第二章基本初等函数(Ⅰ)本章复习Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-30 00:00:00 | ||
图片预览




文档简介
第二章 基本初等函数(Ⅰ)
本章复习
学习目标
①复习巩固指数、对数的运算性质,进一步熟练地运用指数函数、对数函数及幂函数的性质解决一些问题;
②在学生对教材知识掌握的基础上,引导学生利用所学的知识解决问题,提高学生分析问题与解决问题的能力.
合作学习
一、复习回顾,承上启下
1.n次方根的定义:
n次方根:如果xn=a,那么x叫做a的n次方根,其中n>1,且n∈N*.
2.n次方根的性质
(1)当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,记为 ;?
(2)当n为偶数时,正数的n次方根有两个,它们互为相反数,记为 ;?
(3)负数没有偶次方根,0的任何次方根都是0.
3.
4.有理数指数幂的运算性质
an=(n∈N*);a0=1(a≠0);a-n=(a≠0,n∈N*).
(1)am·an=am+n(m,n∈Q);
(2)(am)n=amn(m,n∈Q);
(3)(ab)n=an·bn(n∈Q).
其中am÷an=am·a-n=am-n,()n=(a·b-1)n=an·b-n=.
5.对数:如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作 .其中a叫做对数的底数,N叫做真数.?
根据对数的定义,可以得到对数与指数间的关系:
当a>0,且a≠1时,ax=N?x=logaN(符号功能)——熟练转化;
常用对数:以10为底log10N写成 ;?
自然对数:以e为底logeN写成 (e=2.71828…).?
6.对数的性质
(1)在对数式中N=ax>0(负数和零没有对数);
(2)loga1=0,logaa=1(1的对数等于0,底数的对数等于1);
(3)如果把ab=N中的b写成 ,则有=N(对数恒等式).?
7.对数的运算性质:如果a>0,且a≠1,M>0,N>0,那么:
(1)loga(M·N)= ;?
(2)loga= ;?
(3)logaMn= ;?
(4)logab=(a>0,且a≠1;c>0,且c≠1;b>0)(换底公式);
(5)logab= ;?
(6)lobn= .?
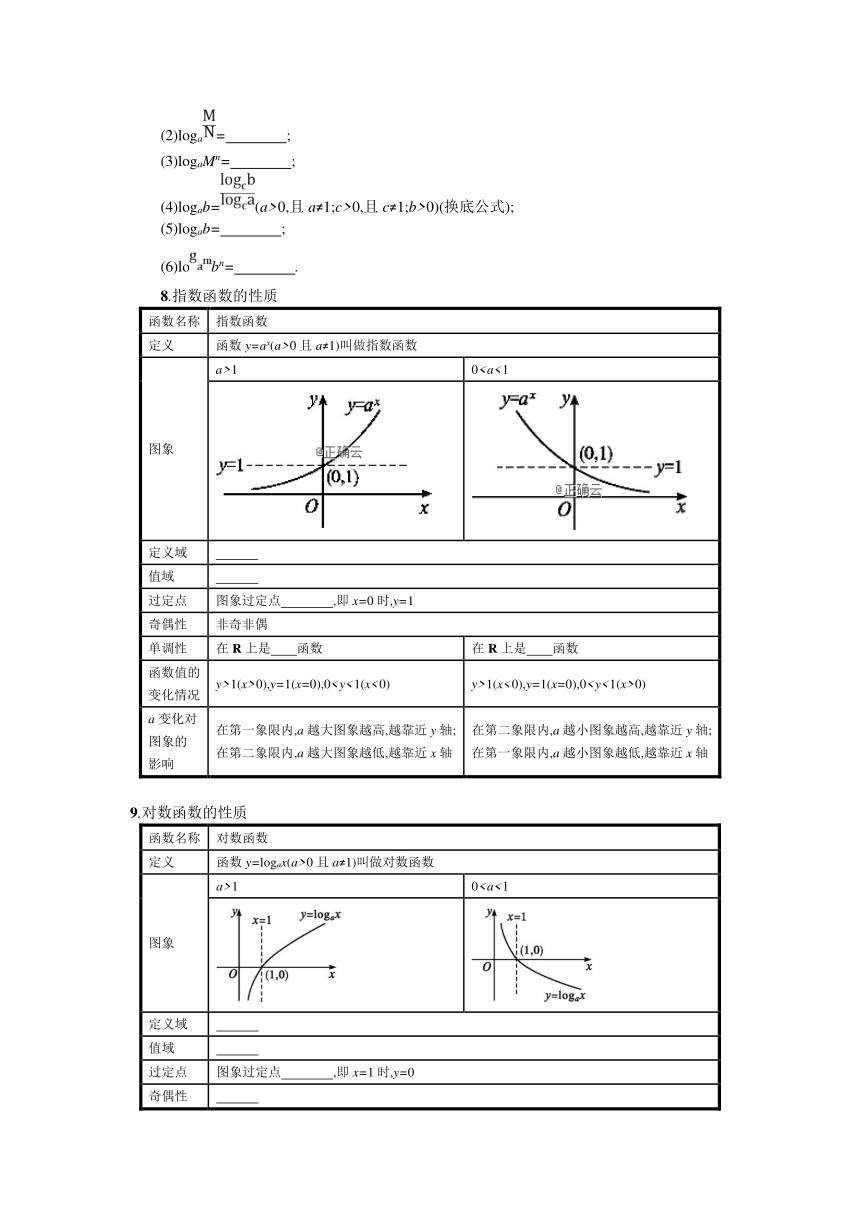
8.指数函数的性质
函数名称
指数函数
定义
函数y=ax(a>0且a≠1)叫做指数函数
图象
a>1
0定义域
?
值域
?
过定点
图象过定点 ,即x=0时,y=1?
奇偶性
非奇非偶
单调性
在R上是 函数?
在R上是 函数?
函数值的
变化情况
y>1(x>0),y=1(x=0),0y>1(x<0),y=1(x=0),00)
a变化对
图象的
影响
在第一象限内,a越大图象越高,越靠近y轴;
在第二象限内,a越大图象越低,越靠近x轴
在第二象限内,a越小图象越高,越靠近y轴;
在第一象限内,a越小图象越低,越靠近x轴
9.对数函数的性质
函数名称
对数函数
定义
函数y=logax(a>0且a≠1)叫做对数函数
图象
a>1
0定义域
?
值域
?
过定点
图象过定点 ,即x=1时,y=0?
奇偶性
?
单调性
在(0,+∞)上是 函数?
在(0,+∞)上是 函数?
函数值的
变化情况
logax>0(x>1)
logax=0(x=1)
logax<0(0logax<0(x>1)
logax=0(x=1)
logax>0(0a变化对
图象的
影响
在第一象限内,a越大图象越低,越靠近x轴,
在第四象限内,a越大图象越高,越靠近y轴
在第一象限内,a越小图象越低,越靠近y轴,
在第四象限内,a越小图象越高,越靠近x轴
10.反函数
(1)反函数概念
函数y=ax(x∈R)与对数函数y=logax(x∈(0,+∞))互为反函数.即同底的指数函数与对数函数互为反函数.
(2)反函数的性质
互为反函数的两个函数的图象关于直线 对称.?
11.幂函数
(1)幂函数的定义
一般地,函数 叫做幂函数,其中x是自变量,α是常数.?
(2)幂函数的图象
(3)幂函数的性质
①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于y轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限;
②过定点:所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1);
③单调性:如果α>0,则幂函数的图象过原点,并且在[0,+∞)上为增函数.如果α<0,则幂函数的图象在(0,+∞)上为减函数,在第一象限内,图象无限接近x轴与y轴;
④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当α=(其中p,q互质,p和q∈Z),若p为奇数q为奇数时,则y=是奇函数,若p为奇数q为偶数时,则y=是偶函数,若p为偶数q为奇数时,则y=是非奇非偶函数;
⑤图象特征:幂函数y=xα,x∈(0,+∞),当α>1时,若01,其图象在直线y=x上方;当α<1时,若01,其图象在直线y=x下方.
二、典例分析,性质应用
1.指数、对数运算
熟练掌握指数的定义、运算法则、公式和对数的定义、运算法则.公式是指数、对数函数及其一切运算赖以施行的基础.
【例1】计算下列各式的值.
(1)(0.027-()-2+(2-(-1)0;
(2)lg5(lg8+lg1000)+(lg)2+lg+lg0.06.
【例2】设4a=5b=100,求2()的值.
【例3】(选讲)已知f(x)=,且0(1)求f(a)+f(1-a)的值;
(2)求f()+f()+f()+…+f()的值.
说明:如果函数f(x)=,则函数f(x)满足f(x)+f(1-x)=1.
2.指数函数、对数函数、幂函数的图象
熟悉指数函数、对数函数、幂函数的图象与性质是熟练求解指、对、幂问题的关键.
【例4】已知c<0,下列不等式中成立的一个是( )
A.c>2c B.c>()c C.2c<()c D.2c>()c
【例5】方程2x-x2=2x+1的解的个数为 .?
【例6】0.32,log20.3,20.3这三个数之间的大小顺序是( )
A.0.32<20.3C.log20.3<0.32<20.3 D.log20.3<20.3<0.32
【例7】方程log3x+x=3的解所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,+∞)
【例8】函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是( )
3.指数函数、对数函数的性质
【例9】比较下列每组中两个数的大小.
(1)2.10.3 2.10.4;(2)()1.3 ()1.6;(3)2.10.3 ()-1.3;(4)log51.9 log52;(5)log0.70.2 log0.52;(6)log42 log34.?
【例10】求下列函数的定义域.
(1)y=;(2)y=;(3)y=lo(3x-2);(4)y=.
【例11】求下列函数的值域.
(1)y=1-2x,x∈[1,4];(2)y=3+log2x,x∈[1,+∞).
【例12】解下列不等式.
(1)<2x-1<4;(2)log0.7(2x)变式:设函数f(x)=若f(x0)<2,求x0的取值范围.
4.指数、对数型复合函数的单调性
指数、对数函数的单调性应用十分广泛,可以用来比较数或式的大小,求函数的定义域、值域、最大值、最小值,求字母参数的取值范围等.
对复合函数y=f[g(x)],若u=g(x)在区间(a,b)上是增函数,其值域为(c,d),又函数y=f(u)在(c,d)上是增函数,那么复合函数在(a,b)上为增函数.可推广为下表(简记为同增异减):
u=g(x)
增
增
减
减
y=f(u)
增
减
增
减
y=f[g(x)]
增
减
减
增
【例13】如果函数f(x)=(a2-1)x在R上是减函数,求实数a的取值范围.
【例14】求下列函数的单调区间.
(1)f(x)=(;(2)y=log5(x2-2x-3).
变式:求下列函数的单调区间.
(1)y=;(2)y=log0.1(2x2-5x-3).
【例15】函数y=loga(x-4)的单调增区间是(4,+∞),求实数a的取值范围.
【例16】(选讲)求函数y=4x+2x+1+3在区间[0,1]上的最大值与最小值.
【例17】求函数y=2lox-lox2+1(≤x≤4)的值域.
5.探究问题
【例18】课本P75习题2.2B组第5题.
(1)试着举几个满足“对定义域内任意实数a,b,都有f(a·b)=f(a)+f(b)”的函数例子,你能说出这些函数具有哪些共同性质吗?
(2)试着举几个满足“对定义域内任意实数a,b,都有f(a+b)=f(a)·f(b)”的函数例子,你能说出这些函数具有哪些共同性质吗?
三、作业精选,巩固提高
1.计算下列各式的值.
(1)lo(3+2);(2)lg25+lg2×lg50;
(3)log6[log4(log381).
2.求下列函数的定义域.
(1)y=;(2)y=;(3)y=;(4)y=loga(x-1)2(03.求下列函数的值域:
(1)y=()x+2,x∈[-1,2];
(2)y=log2(x2-4x-5).
4.求函数y=log2·log2(x∈[1,8])的最大值和最小值.
5.函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和为a,求实数a的值.
6.求下列函数的单调区间.
(1)f(x)=;
(2)f(x)=log4(2x+3-x2);
(3)f(x)=(07.(1)y=lox是减函数,求实数a的取值范围;
(2)若函数f(x)=log0.5(x2-ax+3a)在区间[2,+∞)上是减函数,求实数a的取值范围;
(3)已知函数f(x)=loga(2-ax)在区间[0,1]上是减函数,求实数a的取值范围;
(4)已知f(x)=是(-∞,+∞)上的减函数,求实数a的取值范围.
8.求不等式loga(2x+7)>loga(4x-1)(a>0,且a≠1)中x的取值范围.
9.已知f(x6)=log2x,求f(8).
10.判断函数f(x)=lg(-x)的奇偶性.
11.已知函数f(x)=loga(a>0,且a≠1).
(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性;(3)求不等式f(x)>0的解集.
参考答案
一、复习回顾,承上启下
2.(1)- (2)±
5.x=logaN lgN lnN
6.(3)logaN
7.(1)logaM+logaN
(2)logaM-logaN
(3)nlogaM
(5)
(6)logab
8.R (0,+∞) (0,1) 增 减
9.(0,+∞) R (1,0) 非奇非偶 增 减
10.(2)y=x
11.(1)y=xα
二、典例分析,性质应用
【例1】(1)-45;(2)1.
【例2】2.
【例3】(1)1;(2)500.
【例4】解析:在同一坐标系中分别作出y=x,y=()x,y=2x的图象(如图),显然x<0时,x<2x<()x,即c<0时,c<2c<()c,故选C.
答案:C
【例5】解析:原方程即2x=x2+2x+1,在同一坐标系中画出y=2x,y=x2+2x+1的图象,由图象可知有3个交点.
答案:3
【例6】解析:如图,在同一坐标系中作出函数y=2x,y=x2及y=log2x的图象.观察图象知当x=0.3时,log20.3<0.32<20.3.选C.
答案:C
【例7】解析:直接解方程是无法实现的,而借助数形结合思想作出图象,则问题易于解决.
设y1=log3x,y2=-x+3,在同一坐标系中画出它们的图象(如图),观察可排除A,D.其交点P的横坐标应在(1,3)内.又x=2时,y1=log32<1,而y2=-x+3=1,且知y1是增函数,y2是减函数,所以交点P的横坐标应在(2,3)内,故选C.
答案:C
【例8】解析:f(x)的图象过点(1,1),g(x)的图象过点(0,2),只有C符合,故选C.
答案:C
【例9】(1)<;(2)>;(3)<;(4)<;(5)>;(6)<.
【例10】(1)(-∞,)∪(,+∞);(2)[0,+∞);(3)(,+∞);(4)(5,6].
【例11】(1)[-15,-1];(2)[3,+∞).
【例12】(1)(0,3);(2)(1,+∞).
变式:(-1,1)
【例13】(-,-1)∪(1,)
【例14】(1)减区间:(3,+∞),增区间:(-∞,3);(2)增区间:(3,+∞),减区间:(-∞,-1).
变式:(1)增区间:(1,+∞),减区间:(-∞,1);(2)减区间:(,3),增区间:(-).
【例15】(1,+∞)
【例16】最大值为11,最小值为6.
【例17】解:令lox=u,∵≤x≤4,∴-2≤u≤2,
函数变为y=2u2-2u+1=2(u-)2+(-2≤u≤2).
∴当u=时,ymin=;当u=-2时,ymax=13.
由u=得,x=,由u=-2得,x=4.
∴x=时,函数取最小值,x=4时,函数取最大值13,∴函数的值域为[,13].
【例18】(1)y=log2x,y=log0.3x;(2)y=3x,y=0.1x.
三、作业精选,巩固提高
1.(1)2;(2)1;(3)0.
2.(1)(-∞,0];(2)(-,-];(3)(1,4)∪(4,+∞);(4)(-∞,1)∪(1,+∞);(5)(-1,0)∪(0,2).
3.(1)[,5];(2)R.
4.ymin=-,ymax=2.
5.
6.(1)减区间:(1,+∞),增区间:(-∞,1);(2)增区间:(-1,1),减区间:(1,3);(3)a>1时,增区间:(-1,+∞),减区间:(-∞,-1);a<1时,增区间:(-∞,-1),减区间:(-1,+∞).
7.(1)(-,-1)∪(1,);(2)(-4,4];(3)(1,2);(4)().
8.a>1时,x的取值范围为(,4);09.
10.奇函数
11.(1)(-1,1);(2)奇函数;(3)a>1时,(0,1);0
本章复习
学习目标
①复习巩固指数、对数的运算性质,进一步熟练地运用指数函数、对数函数及幂函数的性质解决一些问题;
②在学生对教材知识掌握的基础上,引导学生利用所学的知识解决问题,提高学生分析问题与解决问题的能力.
合作学习
一、复习回顾,承上启下
1.n次方根的定义:
n次方根:如果xn=a,那么x叫做a的n次方根,其中n>1,且n∈N*.
2.n次方根的性质
(1)当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,记为 ;?
(2)当n为偶数时,正数的n次方根有两个,它们互为相反数,记为 ;?
(3)负数没有偶次方根,0的任何次方根都是0.
3.
4.有理数指数幂的运算性质
an=(n∈N*);a0=1(a≠0);a-n=(a≠0,n∈N*).
(1)am·an=am+n(m,n∈Q);
(2)(am)n=amn(m,n∈Q);
(3)(ab)n=an·bn(n∈Q).
其中am÷an=am·a-n=am-n,()n=(a·b-1)n=an·b-n=.
5.对数:如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作 .其中a叫做对数的底数,N叫做真数.?
根据对数的定义,可以得到对数与指数间的关系:
当a>0,且a≠1时,ax=N?x=logaN(符号功能)——熟练转化;
常用对数:以10为底log10N写成 ;?
自然对数:以e为底logeN写成 (e=2.71828…).?
6.对数的性质
(1)在对数式中N=ax>0(负数和零没有对数);
(2)loga1=0,logaa=1(1的对数等于0,底数的对数等于1);
(3)如果把ab=N中的b写成 ,则有=N(对数恒等式).?
7.对数的运算性质:如果a>0,且a≠1,M>0,N>0,那么:
(1)loga(M·N)= ;?
(2)loga= ;?
(3)logaMn= ;?
(4)logab=(a>0,且a≠1;c>0,且c≠1;b>0)(换底公式);
(5)logab= ;?
(6)lobn= .?
8.指数函数的性质
函数名称
指数函数
定义
函数y=ax(a>0且a≠1)叫做指数函数
图象
a>1
0
?
值域
?
过定点
图象过定点 ,即x=0时,y=1?
奇偶性
非奇非偶
单调性
在R上是 函数?
在R上是 函数?
函数值的
变化情况
y>1(x>0),y=1(x=0),0
a变化对
图象的
影响
在第一象限内,a越大图象越高,越靠近y轴;
在第二象限内,a越大图象越低,越靠近x轴
在第二象限内,a越小图象越高,越靠近y轴;
在第一象限内,a越小图象越低,越靠近x轴
9.对数函数的性质
函数名称
对数函数
定义
函数y=logax(a>0且a≠1)叫做对数函数
图象
a>1
0
?
值域
?
过定点
图象过定点 ,即x=1时,y=0?
奇偶性
?
单调性
在(0,+∞)上是 函数?
在(0,+∞)上是 函数?
函数值的
变化情况
logax>0(x>1)
logax=0(x=1)
logax<0(0
logax=0(x=1)
logax>0(0
图象的
影响
在第一象限内,a越大图象越低,越靠近x轴,
在第四象限内,a越大图象越高,越靠近y轴
在第一象限内,a越小图象越低,越靠近y轴,
在第四象限内,a越小图象越高,越靠近x轴
10.反函数
(1)反函数概念
函数y=ax(x∈R)与对数函数y=logax(x∈(0,+∞))互为反函数.即同底的指数函数与对数函数互为反函数.
(2)反函数的性质
互为反函数的两个函数的图象关于直线 对称.?
11.幂函数
(1)幂函数的定义
一般地,函数 叫做幂函数,其中x是自变量,α是常数.?
(2)幂函数的图象
(3)幂函数的性质
①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于y轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限;
②过定点:所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1);
③单调性:如果α>0,则幂函数的图象过原点,并且在[0,+∞)上为增函数.如果α<0,则幂函数的图象在(0,+∞)上为减函数,在第一象限内,图象无限接近x轴与y轴;
④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当α=(其中p,q互质,p和q∈Z),若p为奇数q为奇数时,则y=是奇函数,若p为奇数q为偶数时,则y=是偶函数,若p为偶数q为奇数时,则y=是非奇非偶函数;
⑤图象特征:幂函数y=xα,x∈(0,+∞),当α>1时,若0
二、典例分析,性质应用
1.指数、对数运算
熟练掌握指数的定义、运算法则、公式和对数的定义、运算法则.公式是指数、对数函数及其一切运算赖以施行的基础.
【例1】计算下列各式的值.
(1)(0.027-()-2+(2-(-1)0;
(2)lg5(lg8+lg1000)+(lg)2+lg+lg0.06.
【例2】设4a=5b=100,求2()的值.
【例3】(选讲)已知f(x)=,且0
(2)求f()+f()+f()+…+f()的值.
说明:如果函数f(x)=,则函数f(x)满足f(x)+f(1-x)=1.
2.指数函数、对数函数、幂函数的图象
熟悉指数函数、对数函数、幂函数的图象与性质是熟练求解指、对、幂问题的关键.
【例4】已知c<0,下列不等式中成立的一个是( )
A.c>2c B.c>()c C.2c<()c D.2c>()c
【例5】方程2x-x2=2x+1的解的个数为 .?
【例6】0.32,log20.3,20.3这三个数之间的大小顺序是( )
A.0.32<20.3
【例7】方程log3x+x=3的解所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,+∞)
【例8】函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是( )
3.指数函数、对数函数的性质
【例9】比较下列每组中两个数的大小.
(1)2.10.3 2.10.4;(2)()1.3 ()1.6;(3)2.10.3 ()-1.3;(4)log51.9 log52;(5)log0.70.2 log0.52;(6)log42 log34.?
【例10】求下列函数的定义域.
(1)y=;(2)y=;(3)y=lo(3x-2);(4)y=.
【例11】求下列函数的值域.
(1)y=1-2x,x∈[1,4];(2)y=3+log2x,x∈[1,+∞).
【例12】解下列不等式.
(1)<2x-1<4;(2)log0.7(2x)
4.指数、对数型复合函数的单调性
指数、对数函数的单调性应用十分广泛,可以用来比较数或式的大小,求函数的定义域、值域、最大值、最小值,求字母参数的取值范围等.
对复合函数y=f[g(x)],若u=g(x)在区间(a,b)上是增函数,其值域为(c,d),又函数y=f(u)在(c,d)上是增函数,那么复合函数在(a,b)上为增函数.可推广为下表(简记为同增异减):
u=g(x)
增
增
减
减
y=f(u)
增
减
增
减
y=f[g(x)]
增
减
减
增
【例13】如果函数f(x)=(a2-1)x在R上是减函数,求实数a的取值范围.
【例14】求下列函数的单调区间.
(1)f(x)=(;(2)y=log5(x2-2x-3).
变式:求下列函数的单调区间.
(1)y=;(2)y=log0.1(2x2-5x-3).
【例15】函数y=loga(x-4)的单调增区间是(4,+∞),求实数a的取值范围.
【例16】(选讲)求函数y=4x+2x+1+3在区间[0,1]上的最大值与最小值.
【例17】求函数y=2lox-lox2+1(≤x≤4)的值域.
5.探究问题
【例18】课本P75习题2.2B组第5题.
(1)试着举几个满足“对定义域内任意实数a,b,都有f(a·b)=f(a)+f(b)”的函数例子,你能说出这些函数具有哪些共同性质吗?
(2)试着举几个满足“对定义域内任意实数a,b,都有f(a+b)=f(a)·f(b)”的函数例子,你能说出这些函数具有哪些共同性质吗?
三、作业精选,巩固提高
1.计算下列各式的值.
(1)lo(3+2);(2)lg25+lg2×lg50;
(3)log6[log4(log381).
2.求下列函数的定义域.
(1)y=;(2)y=;(3)y=;(4)y=loga(x-1)2(0
(1)y=()x+2,x∈[-1,2];
(2)y=log2(x2-4x-5).
4.求函数y=log2·log2(x∈[1,8])的最大值和最小值.
5.函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和为a,求实数a的值.
6.求下列函数的单调区间.
(1)f(x)=;
(2)f(x)=log4(2x+3-x2);
(3)f(x)=(0
(2)若函数f(x)=log0.5(x2-ax+3a)在区间[2,+∞)上是减函数,求实数a的取值范围;
(3)已知函数f(x)=loga(2-ax)在区间[0,1]上是减函数,求实数a的取值范围;
(4)已知f(x)=是(-∞,+∞)上的减函数,求实数a的取值范围.
8.求不等式loga(2x+7)>loga(4x-1)(a>0,且a≠1)中x的取值范围.
9.已知f(x6)=log2x,求f(8).
10.判断函数f(x)=lg(-x)的奇偶性.
11.已知函数f(x)=loga(a>0,且a≠1).
(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性;(3)求不等式f(x)>0的解集.
参考答案
一、复习回顾,承上启下
2.(1)- (2)±
5.x=logaN lgN lnN
6.(3)logaN
7.(1)logaM+logaN
(2)logaM-logaN
(3)nlogaM
(5)
(6)logab
8.R (0,+∞) (0,1) 增 减
9.(0,+∞) R (1,0) 非奇非偶 增 减
10.(2)y=x
11.(1)y=xα
二、典例分析,性质应用
【例1】(1)-45;(2)1.
【例2】2.
【例3】(1)1;(2)500.
【例4】解析:在同一坐标系中分别作出y=x,y=()x,y=2x的图象(如图),显然x<0时,x<2x<()x,即c<0时,c<2c<()c,故选C.
答案:C
【例5】解析:原方程即2x=x2+2x+1,在同一坐标系中画出y=2x,y=x2+2x+1的图象,由图象可知有3个交点.
答案:3
【例6】解析:如图,在同一坐标系中作出函数y=2x,y=x2及y=log2x的图象.观察图象知当x=0.3时,log20.3<0.32<20.3.选C.
答案:C
【例7】解析:直接解方程是无法实现的,而借助数形结合思想作出图象,则问题易于解决.
设y1=log3x,y2=-x+3,在同一坐标系中画出它们的图象(如图),观察可排除A,D.其交点P的横坐标应在(1,3)内.又x=2时,y1=log32<1,而y2=-x+3=1,且知y1是增函数,y2是减函数,所以交点P的横坐标应在(2,3)内,故选C.
答案:C
【例8】解析:f(x)的图象过点(1,1),g(x)的图象过点(0,2),只有C符合,故选C.
答案:C
【例9】(1)<;(2)>;(3)<;(4)<;(5)>;(6)<.
【例10】(1)(-∞,)∪(,+∞);(2)[0,+∞);(3)(,+∞);(4)(5,6].
【例11】(1)[-15,-1];(2)[3,+∞).
【例12】(1)(0,3);(2)(1,+∞).
变式:(-1,1)
【例13】(-,-1)∪(1,)
【例14】(1)减区间:(3,+∞),增区间:(-∞,3);(2)增区间:(3,+∞),减区间:(-∞,-1).
变式:(1)增区间:(1,+∞),减区间:(-∞,1);(2)减区间:(,3),增区间:(-).
【例15】(1,+∞)
【例16】最大值为11,最小值为6.
【例17】解:令lox=u,∵≤x≤4,∴-2≤u≤2,
函数变为y=2u2-2u+1=2(u-)2+(-2≤u≤2).
∴当u=时,ymin=;当u=-2时,ymax=13.
由u=得,x=,由u=-2得,x=4.
∴x=时,函数取最小值,x=4时,函数取最大值13,∴函数的值域为[,13].
【例18】(1)y=log2x,y=log0.3x;(2)y=3x,y=0.1x.
三、作业精选,巩固提高
1.(1)2;(2)1;(3)0.
2.(1)(-∞,0];(2)(-,-];(3)(1,4)∪(4,+∞);(4)(-∞,1)∪(1,+∞);(5)(-1,0)∪(0,2).
3.(1)[,5];(2)R.
4.ymin=-,ymax=2.
5.
6.(1)减区间:(1,+∞),增区间:(-∞,1);(2)增区间:(-1,1),减区间:(1,3);(3)a>1时,增区间:(-1,+∞),减区间:(-∞,-1);a<1时,增区间:(-∞,-1),减区间:(-1,+∞).
7.(1)(-,-1)∪(1,);(2)(-4,4];(3)(1,2);(4)().
8.a>1时,x的取值范围为(,4);0
10.奇函数
11.(1)(-1,1);(2)奇函数;(3)a>1时,(0,1);0
