2019-2020学年高一数学人教A版必修2学案:1.3.1柱体、锥体、台体的表面积和体积Word版含答案
文档属性
| 名称 | 2019-2020学年高一数学人教A版必修2学案:1.3.1柱体、锥体、台体的表面积和体积Word版含答案 | 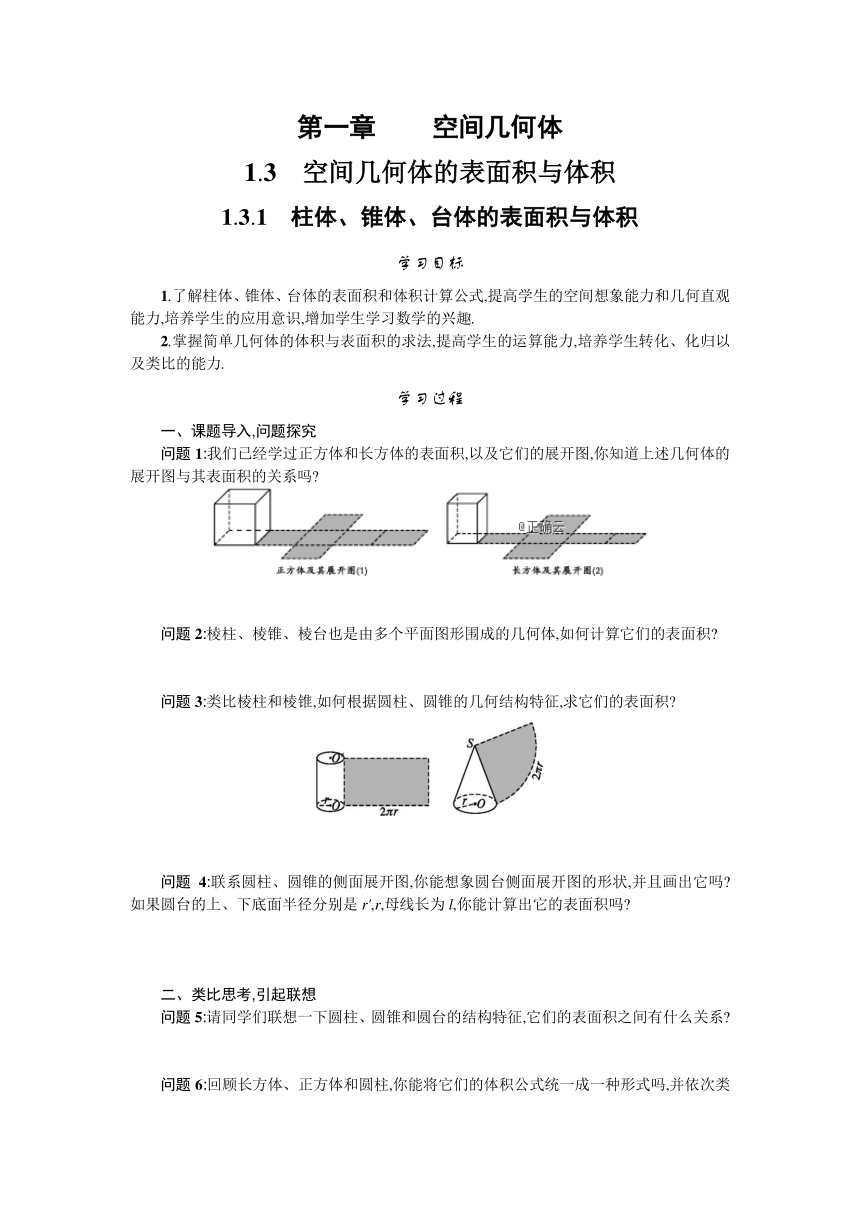 | |
| 格式 | zip | ||
| 文件大小 | 146.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-30 10:25:11 | ||
图片预览


文档简介
空间几何体
1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积与体积
学习目标
1.了解柱体、锥体、台体的表面积和体积计算公式,提高学生的空间想象能力和几何直观能力,培养学生的应用意识,增加学生学习数学的兴趣.
2.掌握简单几何体的体积与表面积的求法,提高学生的运算能力,培养学生转化、化归以及类比的能力.
学习过程
一、课题导入,问题探究
问题1:我们已经学过正方体和长方体的表面积,以及它们的展开图,你知道上述几何体的展开图与其表面积的关系吗?
问题2:棱柱、棱锥、棱台也是由多个平面图形围成的几何体,如何计算它们的表面积?
问题3:类比棱柱和棱锥,如何根据圆柱、圆锥的几何结构特征,求它们的表面积?
问题4:联系圆柱、圆锥的侧面展开图,你能想象圆台侧面展开图的形状,并且画出它吗?如果圆台的上、下底面半径分别是r',r,母线长为l,你能计算出它的表面积吗?
二、类比思考,引起联想
问题5:请同学们联想一下圆柱、圆锥和圆台的结构特征,它们的表面积之间有什么关系?
问题6:回顾长方体、正方体和圆柱,你能将它们的体积公式统一成一种形式吗,并依次类比出柱体的体积公式.
问题7:怎么得到锥体和台体的体积公式呢?
三、典型例题
【例1】若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
A.18 B.15 C.24+8 D.24+16
【例2】已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积.
【例3】(1)两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分的体积的比是( )
A.1∶2∶3 B.1∶7∶19 C.3∶4∶5 D.1∶9∶27
(2)三棱锥V-ABC的中截面是△A1B1C1,则三棱锥V-A1B1C1与三棱锥A-A1BC的体积之比是( )
A.1∶2 B.1∶4 C.1∶6 D.1∶8
【例4】 有一堆规格相同的铁制(铁的密度是7.8 g/cm3)六角螺帽,共重5.8 kg,已知底面是正六边形,边长为12 mm,内孔直径为10 mm,高为10 mm,问这堆螺帽大约有多少个?(π取3.14)
四、作业精选,巩固提高
1.如果一个空间几何体的正视图与侧视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为( )
A. B. C.π D.
2.向高为H的水瓶中匀速注水,注满为止,如果注水量V与水深h的函数关系如图所示,那么水瓶的形状是( )
3.一个圆台的上、下底面面积分别是1 cm2和49 cm2,一个平行于底面的截面面积为25 cm2,则这个截面与上、下底面的距离之比是( )
A.2∶1 B.3∶1 C.∶1 D.∶1
4.已知一圆锥的侧面展开图为半圆,且面积为S,则圆锥的底面面积是 .?
5.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.求
(1)该几何体的体积V;
(2)该几何体的侧面积S.
布置作业
课本P28习题1.3A组第1,2,3题.
参考答案
一、问题1:正方体、长方体是由多个平面图形围成的几何体,它们的表面积就是各个面的面积的和.
问题2:棱柱的侧面展开图是平行四边形,其表面积等于围成棱柱的各个面的面积的和;棱锥的侧面展开图是由多个三角形拼接成的,其表面积等于围成棱锥的各个面的面积的和;棱台的侧面展开图是由多个梯形拼接成的,其表面积等于围成棱台的各个面的面积的和.
问题3:由于它们的底面都是圆面,其底面积直接应用圆的面积公式即可,其中圆柱的侧面展开图是矩形,圆锥的侧面展开图是扇形,利用它们的侧面展开图来求得它们的侧面积,表面积等于侧面积与底面积的和.
如果圆柱的底面半径为r,母线长为l,那么圆柱的底面面积为πr2,侧面面积为2πrl,因此,圆柱的表面积S=2πr2+2πrl=2πr(r+l).如果圆锥的底面半径为r,母线长为l,那么它的表面积S=πr2+πrl=πr(r+l).
(设计意图:将空间图形问题转化为平面图形问题,是解决立体几何问题常用的方法.)
问题4:
圆台的侧面展开图是一个扇环,它的表面积等于上、下两个底面的面积和加上侧面的面积,即S=π(r2+r'2+rl+r'l).
二、问题5:圆柱和圆锥都可以看做是圆台变化而成的几何体,有如下的关系:
S圆柱表=2πr(r+l)S圆台表=π(r1l+r2l+)S圆锥表=πr(r+l).
问题6:柱体的体积是V柱体=Sh(S为底面积,h为柱体的高).
问题7:
锥体的体积公式V锥体=Sh(S为底面积,h为锥体的高).
台体的体积公式V=(S'++S)h,
其中S',S分别为上、下底面面积,h为圆台(棱台)高.
三、【例1】解析:该正三棱柱的直观图如图所示,且底面等边三角形的高为2,正三棱柱的高为2,则底面等边三角形的边长为4,所以该正三棱柱的表面积为3×4×2+2××4×2=24+8.
答案:C
【例2】解:先求△SBC的面积,过点S作SD⊥BC,交BC于点D.
因为BC=a,SD=a,
所以S△SBC=BC·SD=a×a=a2.
因此,四面体S-ABC的表面积S=4×a2=a2.
【例3】 (1)解析:因为圆锥的高被分成的三部分相等,所以两个截面的半径与原圆锥底面半径之比为1∶2∶3,于是自上而下三个圆锥的体积之比为(r2h)∶[(2r)2·2h]∶[(3r)2·3h]=1∶8∶27,所以圆锥被分成的三部分的体积之比为1∶(8-1)∶(27-8)=1∶7∶19.
答案:B
(2)解析:中截面将三棱锥的高分成相等的两部分,所以截面与原底面的面积之比为1∶4,将三棱锥A-A1BC转化为三棱锥A1-ABC,这样三棱锥V-A1B1C1与三棱锥A1-ABC的高相等,底面积之比为1∶4,于是其体积之比为1∶4.
答案:B
【例4】解:六角螺帽的体积是六棱柱体积与圆柱体积的差,即V=×122×6×10-3.14×()2×10≈2 956(mm3)=2.956(cm3).
所以螺帽的个数为5.8×1 000÷(7.8×2.956)≈252(个).
答:这堆螺帽大约有252个.
四、答案:1.A 2.A 3.A 4.
5.解:由三视图可知该几何体是一个底面边长分别为6,8的矩形,高为4的四棱锥,设底面矩形为ABCD,如图所示,AB=8,BC=6,高VO=4.
(1)V=×(8×6)×4=64.
(2)已知四棱锥侧面VAD,VBC是全等的等腰三角形,侧面VAB,VCD也是全等的等腰三角形,
在△VBC中,BC边上的高为h1==4,
在△VAB中,AB边上的高为h2==5.
所以此几何体的侧面积S=2(×6×4×8×5)=40+24.
1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积与体积
学习目标
1.了解柱体、锥体、台体的表面积和体积计算公式,提高学生的空间想象能力和几何直观能力,培养学生的应用意识,增加学生学习数学的兴趣.
2.掌握简单几何体的体积与表面积的求法,提高学生的运算能力,培养学生转化、化归以及类比的能力.
学习过程
一、课题导入,问题探究
问题1:我们已经学过正方体和长方体的表面积,以及它们的展开图,你知道上述几何体的展开图与其表面积的关系吗?
问题2:棱柱、棱锥、棱台也是由多个平面图形围成的几何体,如何计算它们的表面积?
问题3:类比棱柱和棱锥,如何根据圆柱、圆锥的几何结构特征,求它们的表面积?
问题4:联系圆柱、圆锥的侧面展开图,你能想象圆台侧面展开图的形状,并且画出它吗?如果圆台的上、下底面半径分别是r',r,母线长为l,你能计算出它的表面积吗?
二、类比思考,引起联想
问题5:请同学们联想一下圆柱、圆锥和圆台的结构特征,它们的表面积之间有什么关系?
问题6:回顾长方体、正方体和圆柱,你能将它们的体积公式统一成一种形式吗,并依次类比出柱体的体积公式.
问题7:怎么得到锥体和台体的体积公式呢?
三、典型例题
【例1】若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
A.18 B.15 C.24+8 D.24+16
【例2】已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积.
【例3】(1)两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分的体积的比是( )
A.1∶2∶3 B.1∶7∶19 C.3∶4∶5 D.1∶9∶27
(2)三棱锥V-ABC的中截面是△A1B1C1,则三棱锥V-A1B1C1与三棱锥A-A1BC的体积之比是( )
A.1∶2 B.1∶4 C.1∶6 D.1∶8
【例4】 有一堆规格相同的铁制(铁的密度是7.8 g/cm3)六角螺帽,共重5.8 kg,已知底面是正六边形,边长为12 mm,内孔直径为10 mm,高为10 mm,问这堆螺帽大约有多少个?(π取3.14)
四、作业精选,巩固提高
1.如果一个空间几何体的正视图与侧视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为( )
A. B. C.π D.
2.向高为H的水瓶中匀速注水,注满为止,如果注水量V与水深h的函数关系如图所示,那么水瓶的形状是( )
3.一个圆台的上、下底面面积分别是1 cm2和49 cm2,一个平行于底面的截面面积为25 cm2,则这个截面与上、下底面的距离之比是( )
A.2∶1 B.3∶1 C.∶1 D.∶1
4.已知一圆锥的侧面展开图为半圆,且面积为S,则圆锥的底面面积是 .?
5.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.求
(1)该几何体的体积V;
(2)该几何体的侧面积S.
布置作业
课本P28习题1.3A组第1,2,3题.
参考答案
一、问题1:正方体、长方体是由多个平面图形围成的几何体,它们的表面积就是各个面的面积的和.
问题2:棱柱的侧面展开图是平行四边形,其表面积等于围成棱柱的各个面的面积的和;棱锥的侧面展开图是由多个三角形拼接成的,其表面积等于围成棱锥的各个面的面积的和;棱台的侧面展开图是由多个梯形拼接成的,其表面积等于围成棱台的各个面的面积的和.
问题3:由于它们的底面都是圆面,其底面积直接应用圆的面积公式即可,其中圆柱的侧面展开图是矩形,圆锥的侧面展开图是扇形,利用它们的侧面展开图来求得它们的侧面积,表面积等于侧面积与底面积的和.
如果圆柱的底面半径为r,母线长为l,那么圆柱的底面面积为πr2,侧面面积为2πrl,因此,圆柱的表面积S=2πr2+2πrl=2πr(r+l).如果圆锥的底面半径为r,母线长为l,那么它的表面积S=πr2+πrl=πr(r+l).
(设计意图:将空间图形问题转化为平面图形问题,是解决立体几何问题常用的方法.)
问题4:
圆台的侧面展开图是一个扇环,它的表面积等于上、下两个底面的面积和加上侧面的面积,即S=π(r2+r'2+rl+r'l).
二、问题5:圆柱和圆锥都可以看做是圆台变化而成的几何体,有如下的关系:
S圆柱表=2πr(r+l)S圆台表=π(r1l+r2l+)S圆锥表=πr(r+l).
问题6:柱体的体积是V柱体=Sh(S为底面积,h为柱体的高).
问题7:
锥体的体积公式V锥体=Sh(S为底面积,h为锥体的高).
台体的体积公式V=(S'++S)h,
其中S',S分别为上、下底面面积,h为圆台(棱台)高.
三、【例1】解析:该正三棱柱的直观图如图所示,且底面等边三角形的高为2,正三棱柱的高为2,则底面等边三角形的边长为4,所以该正三棱柱的表面积为3×4×2+2××4×2=24+8.
答案:C
【例2】解:先求△SBC的面积,过点S作SD⊥BC,交BC于点D.
因为BC=a,SD=a,
所以S△SBC=BC·SD=a×a=a2.
因此,四面体S-ABC的表面积S=4×a2=a2.
【例3】 (1)解析:因为圆锥的高被分成的三部分相等,所以两个截面的半径与原圆锥底面半径之比为1∶2∶3,于是自上而下三个圆锥的体积之比为(r2h)∶[(2r)2·2h]∶[(3r)2·3h]=1∶8∶27,所以圆锥被分成的三部分的体积之比为1∶(8-1)∶(27-8)=1∶7∶19.
答案:B
(2)解析:中截面将三棱锥的高分成相等的两部分,所以截面与原底面的面积之比为1∶4,将三棱锥A-A1BC转化为三棱锥A1-ABC,这样三棱锥V-A1B1C1与三棱锥A1-ABC的高相等,底面积之比为1∶4,于是其体积之比为1∶4.
答案:B
【例4】解:六角螺帽的体积是六棱柱体积与圆柱体积的差,即V=×122×6×10-3.14×()2×10≈2 956(mm3)=2.956(cm3).
所以螺帽的个数为5.8×1 000÷(7.8×2.956)≈252(个).
答:这堆螺帽大约有252个.
四、答案:1.A 2.A 3.A 4.
5.解:由三视图可知该几何体是一个底面边长分别为6,8的矩形,高为4的四棱锥,设底面矩形为ABCD,如图所示,AB=8,BC=6,高VO=4.
(1)V=×(8×6)×4=64.
(2)已知四棱锥侧面VAD,VBC是全等的等腰三角形,侧面VAB,VCD也是全等的等腰三角形,
在△VBC中,BC边上的高为h1==4,
在△VAB中,AB边上的高为h2==5.
所以此几何体的侧面积S=2(×6×4×8×5)=40+24.
