人教版九年级数学下册 26.1.2 反比例函数的图象和性质 课件(54张)
文档属性
| 名称 | 人教版九年级数学下册 26.1.2 反比例函数的图象和性质 课件(54张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 00:00:00 | ||
图片预览











文档简介
(共54张PPT)
1.什么是反比例函数?
温故而知新
新课导入
一般地,形如 ( k是常数,k≠0 ) 的函数叫做反比例函数.
2.反比例函数的图象是什么?图象的位置由谁决定?分别在哪些象限?
反比例函数的图象是双曲线.
当k>0时,两支双曲线分别位于第一,三象限内,
当k<0时,两支双曲线分别位于第二,四象限内.
那么反比例函数有哪些性质呢?
知识与能力
1.通过对反比例函数的图象和性质的探究,培养观察、比较、类比、联想、分析、归纳、概括的逻辑思维能力以及动手实践能力.
2.通过对反比例函数的图象和性质的探究,培养数形结合、分类讨论的数学思想方法.
3.通过实际问题的解决培养建模能力、创新意识和创新能力.
教学目标
26.1.2 反比例函数的图象和性质
过程与方法
通过经历观察、归纳、交流的过程,探索反比例函数的主要性质及其图像形状.
1.通过实际问题的解决,培养勇于探索、锲而不舍的精神.
2.获得亲自参与研究探索的情感体验,从而增强学习数学的热情.
情感态度与价值观
1.理解并掌握反比例函数的图象和性质,并能利用它们解决一些综合问题.
2.正确画出图象,通过观察、分析,归纳出反比例函数的性质,学会从图象上分析、解决问题.
3.通过观察图象,概括反比例函数图象的共同特征,探索 反比例函数的主要性质.从反比例函数的图象中归纳总结反比例函数的主要性质.
教学重难点
1.一次函数y=kx+b(k、b是常数,k≠0)
的图象是什么?其性质有哪些?
x
y
o
x
y
o
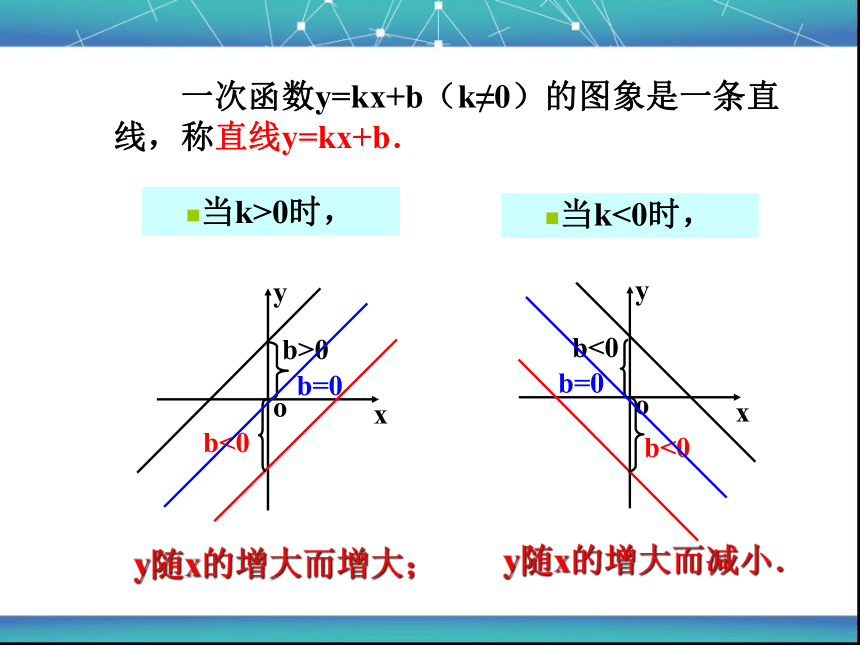
y随x的增大而减小.
b<0
b>0
b=0
b<0
b<0
b=0
当k>0时,
当k<0时,
一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.
y随x的增大而增大;
3.反比例函数的图象是什么样呢?
2.画函数图象的方法是什么?其一般步骤
有哪些?
描点法,一般步骤是列表、描点、连线.
函数图象画法
列
表
描
点
连
线
描点法
(1)这个函数中自变量的取值范围是什么?
(2)画函数图象的三个步骤是什么?
因为分母不能为零,所以 x≠ 0.
例1 画出反比例函数 和 的函数图象.
解:
(1)列表:列表表示几组x与y的对应值.
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
1
2
4
8
-8
-4
-2
-1
1.先作函数 的图象.
作反比例函数图象时应注意的问题:
(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值;
(2)列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
(3)连线时一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,切忌画成折线;
(4)由于x≠0,k≠0,所以y≠0,函数图象永远不会与x轴、y轴相交,只是无限靠近两坐标轴.
(2)描点:以表中各对对应值为坐标,画出各点.
.
.
.
.
.
.
.
.
.
.
.
.
y
-1
x
1
3
2
4
5
6
-6
-4
-5
-3
-2
-1
7
8
-8
-7
-8
0
1
2
3
4
5
6
-6
-5
-3
-4
-2
7
8
-7
(3)连线:用平滑的曲线顺次将这些点连接起来.
x
y
.
-8
0
1
3
2
4
5
6
1
2
3
4
5
6
-6
-6
-5
-3
-4
-1
-2
-4
-5
-3
-2
-1
.
.
.
.
.
.
.
.
.
.
.
7
8
-8
-7
7
8
-7
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
-1
-2
-4
-8
8
4
2
1
(1)列表:列表表示几组x与y的对应值.
2.作出函数 的图象.
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
.
y
x
.
.
.
.
.
.
(2)描点:以表中各对对应值为坐标,画出各点.
.
(3)连线:用平滑的曲线顺次将这些点连接起来.
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
.
y
x
.
.
.
.
.
.
4
y
5
6
1
2
3
-6
-5
-3
-4
-2
1
2
3
4
5
6
-4
-1
-2
-3
-5
-6
-1
0
x
(1)函数 和函数 的图象分别在哪两个象限?
(2)它们之间有什么相同点和不同点?
(1)函数 的图象在第一和第三象限,函数 的图象在第二和第四象限.
(2)它们都由两条曲线组成,并且随着x的不断增大(或减小),曲线越来越接近坐标轴.
在同一直角坐标系内,反比例函数 与
的图象关于x轴对称,也关于y轴对称.
在平面直角坐标系中画出反比例函数
和 的函数图象.
小练习
6
-6
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
1
3
2
4
5
6
6
-6
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
1
3
2
4
5
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
y =
x
6
6
-6
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
1
3
2
4
5
6
y=6/x
y=-6/x
y=6/x
y=-6/x
x
y
0
1
x
y
0
1
k>0
k<0
(2)当 k>0 时,两支曲线分别位于第___、___象限,
(3)当 k<0 时,两支曲线分别位于第___、___象限.
在每一象限内,y的值随x值的增大而 _____;
在每一象限内,y的值随x值的增大而_____.
减小
一
三
二
四
增大
(1)反比例函数 的图象是由________组成
的.
两支曲线
小练习
反比例函数 (k为常数,k≠0) 图象的性质:
(1)反比例函数 (k为常数,k≠0)的图象是双曲线;
(2)当k>0时,双曲线的两个分支分别位于第一、三象限,在每个象限内y值随x值的增大而减小;
当 k<0时,双曲线的两个分支分别位于第二、四象限,在每个象限内y值随x值的增大而增大.
(3)反比例函数 (k为常数,k≠0)的图象关于直角坐标系的原点成中心对称.
知识要点
1.在图中反比例函数的图象大致是( )
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
小练习
D
2.(2019甘肃兰州)老师给出了一个函数,甲、
乙、丙三位学生分别指出了这个函数的一个性
质,
甲:第一象限内有它的图象;
乙:第三象限内有它的图象;
丙:在每个象限内,随的增大而减小.
请你写一个满足上述性质的函数解析________.
3.如图所示:比较k1,k2,k3,k4的大小.
x
y
y=k4/x
y=k2/x
y=k1/x
y=k3/x
k1>k2>k3>k4
双曲线离原点越远k的绝对值越大
双曲线离原点越近k的绝对值越小
(1)求函数的解析式,并说出这个函数的图象分布在哪些象限?y随x的增大如何变化?
例2 已知反比例函数的图象经过点A(2 ,-5)
因为图象经过点(2,-5)
把x=2,y=-5 代入得
所以,
k=-10
解: 设反比例函数解析式为 (k≠0)
因为k<0,所以这个函数的图象在第二、四象限,在每个象限内,y随x的增大而增大.
(3)若点M(5 , a)在该图象上,求a的值.
(2)点B(1,3)、C (2,4)、 D (-5,2)和 E (2.5,-4)是否在这个函数图象上?
解: 因为点M(5 , a)在图象上,把x=5,y= a代入 , 得:
a=-2.
解:把点B、C、D和E的坐标代入 ,可知点D,E的坐标满足函数关系式,点B、点C的坐标不满足函数关系式,所以点D、点E在函数 的图象上,点B、点C不在这个函数的图象上.
(2019新疆乌鲁木齐)若反比例函数 (k为常数,k≠0)的图象经过点(3,-4),则下列各点在该函数图象上的是( )
A.(6,-8) B.(-6,8)
C.(-3,4) D.(-3,-4)
小练习
C
例3 图是反比例函数 的图像的一支.根据图像回答下列问题:
(1)图像的另一支在哪个象限?常数a的取值范围是什么?
(2)在这个函数图像的某一支上任取点A(m,n)和点B(m′,n′) .如果m>m′,那么n和n′有怎样的大小关系?
解:(1)反比例函数图像的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限.这个函数的图像的一支在第一象限,则另一支必在第三象限.
因为这个函数的图像分布在第一、第三象限,
所以 a+6>0
解得 a>-6
(2)因为a+6>0,在这个函数图像的任一支上,y随x的增大而减小,
所以当m>m′时,n1.(2019山东泰安)已知三点P1(x1,y1),
P2(x2,y2),P3(1,-2),都在反比例函
数 的图象上,若x1<0,x2>0,则下列
式子正确的是( )
A.y1C.y1>y2>0 D.y1>0>y2
小练习
D
2.已知反比例函数 的图象在第
二、四象限,求m值,并指出在每个象限内y
随x的变化情况?
解:∵是反比例函数
∴m2-5=-1,且m-1≠0,
∴m=±2
又∵图象在第二、四象限 ∴m-1<0
解得且m<1
∴m= -2
例4 在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的面积为S1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的面积为S2,S1与S2有什么关系?为什么?
解:(1)设P(m,n)是双曲线 (k≠0) 上任意一点,过P分别作x轴,y轴的垂线,垂足分别为A、B,则
S矩形OAPB=OA·OB=|m|·|m|=|k|
(2)设P(m,n)是双曲线 (k≠0)上任意一点,过P作x轴的垂线,垂足为A,则
S△OAP= OA·OP= |m|·|m|= |k|
1.如图,过反比例函数 (x>0)的图象上
任意两点A、B分别作x轴的垂线,垂足分别为
C、D,连接OA、OB,设△AOC和△BOD的
面积分别是S1、S2,比较它们的大小,可得
( )
A.S1>S2
B.S1=S2
C.S1<S2
D.大小关系不能确定
B
小练习
A
C
o
y
x
P
2.如图,P是反比例函数图象上的一点,由P
分别向x轴,y轴引垂线,阴影部分面积为
3,求这个反比例函数的解析式.
解:S矩形OAPB=|k|,∴|k|=3,
又因为图象在第二象限,
∴k= -3,
∴此反比例函数的解析式为
3.反比例函数y=m/x与一次函数y=kx+b交于点
A(1,8),和B(4,2),则三角形AOB
的面积是________
y
x
o
A
B
15
4.(2019年铜仁中考)如图所示:p在反比例
函数y=2/x上,P点关于原点对称的点是P1,
过P,P1作x轴,y轴的平行线交于点Q,则
△PP1Q的面积是 ____.
y
x
o
P
P1
Q
4
正比例函数和反比例函数的区别
函数名称 正比例函数 反比例函数
函数解析式和自变量取值范围
图像
性质
k<0
k<0
k>0
k>0
o
x
y
o
x
y
x取不为0的
所有实数
o
x
y
o
x
y
y随着x增大而增大
y随着x增大而减小
在每一象限
内, y随着
x增大而增大
在每一象限
内,y随着
x增大而减小
y=kx(k≠0)
x取一切实数
反比例函数的图象和性质:
(1)反比例函数的图象是双曲线;
(2)图象性质:
k>0
k<0
图象
课堂小结
k>0
k<0
当k>0时,函数图象的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小.
当k<0时,函数图象的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大.
性质
(3)在反比例函数图象上任取一点,过这一点分别作x轴、y轴的平行线,与坐标轴围成的面积总等于常量∣K∣.
1.已知反比例函数
(1)若函数的图象位于第一三象限,则k_______;
(2)若在每一象限内,y随x增大而增大,
则k_______.
<6
>6
随堂练习
2.(1)函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
(2)函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
一、三
二、四
减小
增大
x
y
o
x
y
o
x
y
o
x
y
o
A B C D
3.函数y=kx-k 与 在同一条直角坐标
系中的图象可能是( )
D
x
y
0
x
y
0
x
y
0
x
y
0
A
B
C
D
D
4. 已知k<0,则函数 y1=kx,y2= 在同一坐标
系中的图象大致是 ( )
A
x
y
0
x
y
0
B
C
D
x
y
0
x
y
0
C
5. 已知k>0,则函数 y1=kx+k与y2= 在同一坐
标系中的图象大致是( )
6.若直线y=kx+b经过第一、二、四象限,则
函数 的图象在( )
B
A.第一、三象限
B.第二、四象限
C.第三、四象限
D.第一、二象限
7.已知点(-1,y1)、(2,y2)、(3,y3)
在双曲线 上,则下列关系式正确的
是( )
B
A.y1>y2>y3
B.y1>y3>y2
C.y2>y1>y3
D.y3>y1>y2
8.已知一次函数y=kx+b的图像与反比例函数
的图像交于A、B两点,且点A的横坐
标和点B的纵坐标都是-2 ,则一次函数的解
析式是_______;△AOB的面积是________.
y=-x+2
6
9.已知反比例函数y=mxm?-5 ,它的两个分支分
别在第一、第三象限,求m的值?
解:因为反比例函数y=mxm?-5 ,它的两个分支分别在第一、第三象限,
m﹥0
m?-5= -1
得 m = 2
y=mxm?-5
所以必须满足
x
y
o
1.什么是反比例函数?
温故而知新
新课导入
一般地,形如 ( k是常数,k≠0 ) 的函数叫做反比例函数.
2.反比例函数的图象是什么?图象的位置由谁决定?分别在哪些象限?
反比例函数的图象是双曲线.
当k>0时,两支双曲线分别位于第一,三象限内,
当k<0时,两支双曲线分别位于第二,四象限内.
那么反比例函数有哪些性质呢?
知识与能力
1.通过对反比例函数的图象和性质的探究,培养观察、比较、类比、联想、分析、归纳、概括的逻辑思维能力以及动手实践能力.
2.通过对反比例函数的图象和性质的探究,培养数形结合、分类讨论的数学思想方法.
3.通过实际问题的解决培养建模能力、创新意识和创新能力.
教学目标
26.1.2 反比例函数的图象和性质
过程与方法
通过经历观察、归纳、交流的过程,探索反比例函数的主要性质及其图像形状.
1.通过实际问题的解决,培养勇于探索、锲而不舍的精神.
2.获得亲自参与研究探索的情感体验,从而增强学习数学的热情.
情感态度与价值观
1.理解并掌握反比例函数的图象和性质,并能利用它们解决一些综合问题.
2.正确画出图象,通过观察、分析,归纳出反比例函数的性质,学会从图象上分析、解决问题.
3.通过观察图象,概括反比例函数图象的共同特征,探索 反比例函数的主要性质.从反比例函数的图象中归纳总结反比例函数的主要性质.
教学重难点
1.一次函数y=kx+b(k、b是常数,k≠0)
的图象是什么?其性质有哪些?
x
y
o
x
y
o
y随x的增大而减小.
b<0
b>0
b=0
b<0
b<0
b=0
当k>0时,
当k<0时,
一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.
y随x的增大而增大;
3.反比例函数的图象是什么样呢?
2.画函数图象的方法是什么?其一般步骤
有哪些?
描点法,一般步骤是列表、描点、连线.
函数图象画法
列
表
描
点
连
线
描点法
(1)这个函数中自变量的取值范围是什么?
(2)画函数图象的三个步骤是什么?
因为分母不能为零,所以 x≠ 0.
例1 画出反比例函数 和 的函数图象.
解:
(1)列表:列表表示几组x与y的对应值.
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
1
2
4
8
-8
-4
-2
-1
1.先作函数 的图象.
作反比例函数图象时应注意的问题:
(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值;
(2)列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
(3)连线时一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,切忌画成折线;
(4)由于x≠0,k≠0,所以y≠0,函数图象永远不会与x轴、y轴相交,只是无限靠近两坐标轴.
(2)描点:以表中各对对应值为坐标,画出各点.
.
.
.
.
.
.
.
.
.
.
.
.
y
-1
x
1
3
2
4
5
6
-6
-4
-5
-3
-2
-1
7
8
-8
-7
-8
0
1
2
3
4
5
6
-6
-5
-3
-4
-2
7
8
-7
(3)连线:用平滑的曲线顺次将这些点连接起来.
x
y
.
-8
0
1
3
2
4
5
6
1
2
3
4
5
6
-6
-6
-5
-3
-4
-1
-2
-4
-5
-3
-2
-1
.
.
.
.
.
.
.
.
.
.
.
7
8
-8
-7
7
8
-7
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
-1
-2
-4
-8
8
4
2
1
(1)列表:列表表示几组x与y的对应值.
2.作出函数 的图象.
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
.
y
x
.
.
.
.
.
.
(2)描点:以表中各对对应值为坐标,画出各点.
.
(3)连线:用平滑的曲线顺次将这些点连接起来.
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
.
y
x
.
.
.
.
.
.
4
y
5
6
1
2
3
-6
-5
-3
-4
-2
1
2
3
4
5
6
-4
-1
-2
-3
-5
-6
-1
0
x
(1)函数 和函数 的图象分别在哪两个象限?
(2)它们之间有什么相同点和不同点?
(1)函数 的图象在第一和第三象限,函数 的图象在第二和第四象限.
(2)它们都由两条曲线组成,并且随着x的不断增大(或减小),曲线越来越接近坐标轴.
在同一直角坐标系内,反比例函数 与
的图象关于x轴对称,也关于y轴对称.
在平面直角坐标系中画出反比例函数
和 的函数图象.
小练习
6
-6
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
1
3
2
4
5
6
6
-6
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
1
3
2
4
5
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
y =
x
6
6
-6
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
1
3
2
4
5
6
y=6/x
y=-6/x
y=6/x
y=-6/x
x
y
0
1
x
y
0
1
k>0
k<0
(2)当 k>0 时,两支曲线分别位于第___、___象限,
(3)当 k<0 时,两支曲线分别位于第___、___象限.
在每一象限内,y的值随x值的增大而 _____;
在每一象限内,y的值随x值的增大而_____.
减小
一
三
二
四
增大
(1)反比例函数 的图象是由________组成
的.
两支曲线
小练习
反比例函数 (k为常数,k≠0) 图象的性质:
(1)反比例函数 (k为常数,k≠0)的图象是双曲线;
(2)当k>0时,双曲线的两个分支分别位于第一、三象限,在每个象限内y值随x值的增大而减小;
当 k<0时,双曲线的两个分支分别位于第二、四象限,在每个象限内y值随x值的增大而增大.
(3)反比例函数 (k为常数,k≠0)的图象关于直角坐标系的原点成中心对称.
知识要点
1.在图中反比例函数的图象大致是( )
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
小练习
D
2.(2019甘肃兰州)老师给出了一个函数,甲、
乙、丙三位学生分别指出了这个函数的一个性
质,
甲:第一象限内有它的图象;
乙:第三象限内有它的图象;
丙:在每个象限内,随的增大而减小.
请你写一个满足上述性质的函数解析________.
3.如图所示:比较k1,k2,k3,k4的大小.
x
y
y=k4/x
y=k2/x
y=k1/x
y=k3/x
k1>k2>k3>k4
双曲线离原点越远k的绝对值越大
双曲线离原点越近k的绝对值越小
(1)求函数的解析式,并说出这个函数的图象分布在哪些象限?y随x的增大如何变化?
例2 已知反比例函数的图象经过点A(2 ,-5)
因为图象经过点(2,-5)
把x=2,y=-5 代入得
所以,
k=-10
解: 设反比例函数解析式为 (k≠0)
因为k<0,所以这个函数的图象在第二、四象限,在每个象限内,y随x的增大而增大.
(3)若点M(5 , a)在该图象上,求a的值.
(2)点B(1,3)、C (2,4)、 D (-5,2)和 E (2.5,-4)是否在这个函数图象上?
解: 因为点M(5 , a)在图象上,把x=5,y= a代入 , 得:
a=-2.
解:把点B、C、D和E的坐标代入 ,可知点D,E的坐标满足函数关系式,点B、点C的坐标不满足函数关系式,所以点D、点E在函数 的图象上,点B、点C不在这个函数的图象上.
(2019新疆乌鲁木齐)若反比例函数 (k为常数,k≠0)的图象经过点(3,-4),则下列各点在该函数图象上的是( )
A.(6,-8) B.(-6,8)
C.(-3,4) D.(-3,-4)
小练习
C
例3 图是反比例函数 的图像的一支.根据图像回答下列问题:
(1)图像的另一支在哪个象限?常数a的取值范围是什么?
(2)在这个函数图像的某一支上任取点A(m,n)和点B(m′,n′) .如果m>m′,那么n和n′有怎样的大小关系?
解:(1)反比例函数图像的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限.这个函数的图像的一支在第一象限,则另一支必在第三象限.
因为这个函数的图像分布在第一、第三象限,
所以 a+6>0
解得 a>-6
(2)因为a+6>0,在这个函数图像的任一支上,y随x的增大而减小,
所以当m>m′时,n
P2(x2,y2),P3(1,-2),都在反比例函
数 的图象上,若x1<0,x2>0,则下列
式子正确的是( )
A.y1
小练习
D
2.已知反比例函数 的图象在第
二、四象限,求m值,并指出在每个象限内y
随x的变化情况?
解:∵是反比例函数
∴m2-5=-1,且m-1≠0,
∴m=±2
又∵图象在第二、四象限 ∴m-1<0
解得且m<1
∴m= -2
例4 在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的面积为S1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的面积为S2,S1与S2有什么关系?为什么?
解:(1)设P(m,n)是双曲线 (k≠0) 上任意一点,过P分别作x轴,y轴的垂线,垂足分别为A、B,则
S矩形OAPB=OA·OB=|m|·|m|=|k|
(2)设P(m,n)是双曲线 (k≠0)上任意一点,过P作x轴的垂线,垂足为A,则
S△OAP= OA·OP= |m|·|m|= |k|
1.如图,过反比例函数 (x>0)的图象上
任意两点A、B分别作x轴的垂线,垂足分别为
C、D,连接OA、OB,设△AOC和△BOD的
面积分别是S1、S2,比较它们的大小,可得
( )
A.S1>S2
B.S1=S2
C.S1<S2
D.大小关系不能确定
B
小练习
A
C
o
y
x
P
2.如图,P是反比例函数图象上的一点,由P
分别向x轴,y轴引垂线,阴影部分面积为
3,求这个反比例函数的解析式.
解:S矩形OAPB=|k|,∴|k|=3,
又因为图象在第二象限,
∴k= -3,
∴此反比例函数的解析式为
3.反比例函数y=m/x与一次函数y=kx+b交于点
A(1,8),和B(4,2),则三角形AOB
的面积是________
y
x
o
A
B
15
4.(2019年铜仁中考)如图所示:p在反比例
函数y=2/x上,P点关于原点对称的点是P1,
过P,P1作x轴,y轴的平行线交于点Q,则
△PP1Q的面积是 ____.
y
x
o
P
P1
Q
4
正比例函数和反比例函数的区别
函数名称 正比例函数 反比例函数
函数解析式和自变量取值范围
图像
性质
k<0
k<0
k>0
k>0
o
x
y
o
x
y
x取不为0的
所有实数
o
x
y
o
x
y
y随着x增大而增大
y随着x增大而减小
在每一象限
内, y随着
x增大而增大
在每一象限
内,y随着
x增大而减小
y=kx(k≠0)
x取一切实数
反比例函数的图象和性质:
(1)反比例函数的图象是双曲线;
(2)图象性质:
k>0
k<0
图象
课堂小结
k>0
k<0
当k>0时,函数图象的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小.
当k<0时,函数图象的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大.
性质
(3)在反比例函数图象上任取一点,过这一点分别作x轴、y轴的平行线,与坐标轴围成的面积总等于常量∣K∣.
1.已知反比例函数
(1)若函数的图象位于第一三象限,则k_______;
(2)若在每一象限内,y随x增大而增大,
则k_______.
<6
>6
随堂练习
2.(1)函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
(2)函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
一、三
二、四
减小
增大
x
y
o
x
y
o
x
y
o
x
y
o
A B C D
3.函数y=kx-k 与 在同一条直角坐标
系中的图象可能是( )
D
x
y
0
x
y
0
x
y
0
x
y
0
A
B
C
D
D
4. 已知k<0,则函数 y1=kx,y2= 在同一坐标
系中的图象大致是 ( )
A
x
y
0
x
y
0
B
C
D
x
y
0
x
y
0
C
5. 已知k>0,则函数 y1=kx+k与y2= 在同一坐
标系中的图象大致是( )
6.若直线y=kx+b经过第一、二、四象限,则
函数 的图象在( )
B
A.第一、三象限
B.第二、四象限
C.第三、四象限
D.第一、二象限
7.已知点(-1,y1)、(2,y2)、(3,y3)
在双曲线 上,则下列关系式正确的
是( )
B
A.y1>y2>y3
B.y1>y3>y2
C.y2>y1>y3
D.y3>y1>y2
8.已知一次函数y=kx+b的图像与反比例函数
的图像交于A、B两点,且点A的横坐
标和点B的纵坐标都是-2 ,则一次函数的解
析式是_______;△AOB的面积是________.
y=-x+2
6
9.已知反比例函数y=mxm?-5 ,它的两个分支分
别在第一、第三象限,求m的值?
解:因为反比例函数y=mxm?-5 ,它的两个分支分别在第一、第三象限,
m﹥0
m?-5= -1
得 m = 2
y=mxm?-5
所以必须满足
x
y
o
