2019-2020学年北师大版数学选修1-1第4章4.1.2导数应用课件:54张PPT
文档属性
| 名称 | 2019-2020学年北师大版数学选修1-1第4章4.1.2导数应用课件:54张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-30 10:13:50 | ||
图片预览










文档简介
课件54张PPT。第四章导数应用§1 函数的单调性与极值1.2 函数的极值自主预习学案
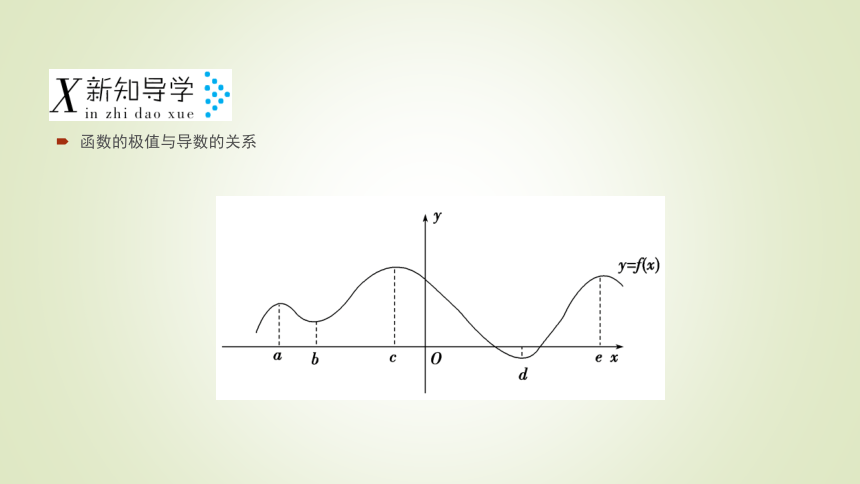
函数的极值与导数的关系(1)如图是函数y=f(x)的图像,在x=a邻近的左侧f(x)单调递__________,f ′(x)__________0,右侧f(x)单调递__________,_f ′(x)__________0,在x=a邻近的函数值都比f(a)小,且f ′(a)__________0.在x=b邻近情形恰好相反,图形上与a类似的点还有__________,(e,f(e)),与b类似的点还有__________.
我们把点a叫作函数f(x)的极__________值点,f(a)是函数的一个极__________值;把点b叫作函数f(x)的极__________值点,f(b)是函数的一个极__________值.增 > 减 < = (c,_f(c)) (d,f(d)) 大 大 小 小 (2)一般地,已知函数y=f(x)及其定义域内一点x0,对于包含x0在内的开区间(a,b)内的所有点x,如果都有_____________,则称函数f(x)在点x0处取得__________,并把x0称为函数f(x)的一个______________;如果都有__________,则称函数f(x)在点x0处取得__________,并把x0称为函数f(x)的一个__________.极大值与极小值统称为__________,极大值点与极小值点统称为__________.f(x)f(x0) 极小值 极小值点 极值 极值点 1.按定义,极值点x0是区间[a,b]内部的点,不会是端点a,b.
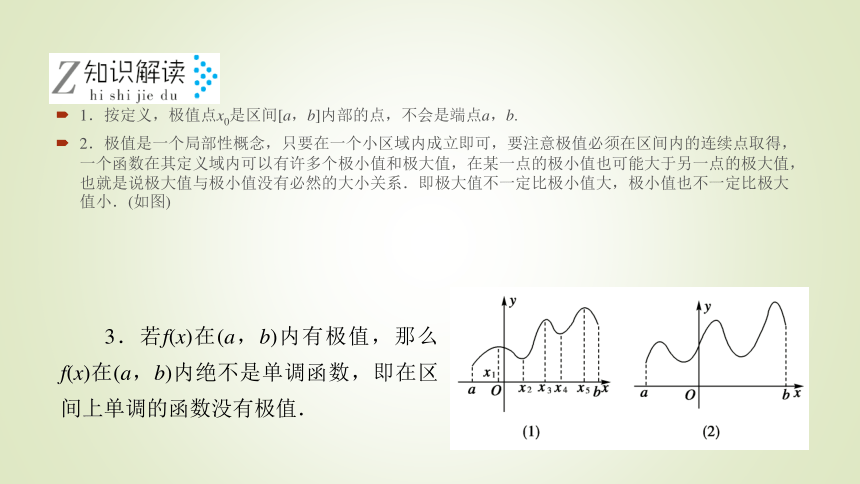
2.极值是一个局部性概念,只要在一个小区域内成立即可,要注意极值必须在区间内的连续点取得,一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值也可能大于另一点的极大值,也就是说极大值与极小值没有必然的大小关系.即极大值不一定比极小值大,极小值也不一定比极大值小.(如图)3.若f(x)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在区间上单调的函数没有极值. 1.函数y=x3+1的极大值是( )
A.1 B.0
C.2 D.不存在
[解析] ∵y′=3x2≥0在R上恒成立,
∴函数y=x3+1在R上是单调增函数,
∴函数y=x3+1无极值.D2.下列说法正确的是( )
A.函数在闭区间上的极大值一定比极小值大
B.函数在闭区间上的极大值一定比极小值小
C.函数f(x)=|x|只有一个极小值
D.函数y=f(x)在区间(a,b)上一定存在极值
[解析] 函数的极大值与极小值之间无确定的大小关系,单调函数在区间(a,b)上没有极值,故A,B,D错误,C正确,函数f(x)=|x|只有一个极小值为0.C3.函数f(x)的定义域为开区间(a,b),导函数f ′(x)在(a,b)内的图像如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
A.1个
B.2个
C.3个
D.4个A5.已知k为实数, f(x)=(x2-4)(x+k).
(1)求导函数f ′(x);
(2)若x=-1是函数f(x)的极值点,求y=f(x)在区间[-2,2]上的极值.互动探究学案 求函数y=3x3-x+1的极值.
[思路分析] 首先对函数求导,然后求方程y′=0的根,再检查y′在方程根左右的值的符号.如果左正右负,那么y在这个根处取得极大值;如果左负右正,那么y在这个根处取得极小值.命题方向1 ?利用导数求函数的极值典例 1 『规律方法』 1.当函数f(x)在点x0处连续时,判断f(x0)是否为极大(小)值的方法是:
(1)如果在x0附近的左侧f ′(x)>0,右侧f ′(x)<0,那么f(x0)是极大值;
(2)如果在x0附近的左侧f ′(x)<0,右侧f ′(x)>0,那么f(x0)是极小值;
(3)如果f ′(x)在点x0的左、右两侧符号不变,则f(x0)不是函数f(x)的极值.
2.利用导数求函数极值的步骤:
(1)确定函数的定义域.
(2)求导数f ′(x).
(3)解方程f ′(x)=0得方程的根.
(4)利用方程f ′(x)=0的根将定义域分成若干个小开区间,列表,判定导函数在各个小开区间的符号.
〔跟踪练习1〕
设函数f(x)=x3+ax2-9x的导函数为f ′(x),且f ′(2)=15.
(1)求函数f(x)的图像在x=0处的切线方程;
(2)求函数f(x)的极值.
[解析] (1)∵f ′(x)=3x2+2ax-9,
∵f ′(2)=15,∴12+4a-9=15,∴a=3.
∴f(x)=x3+3x2-9x,
∴f ′(x)=3x2+6x-9,
∴f(0)=0,f ′(0)=-9,
∴函数在x=0处的切线方程为y=-9x. 已知函数f(x)=ax4·ln x+bx4-c(x>0).在x=1处取得极值-3-c,其中a、b为常数.
(1)试确定a、b的值;
(2)讨论函数f(x)的单调区间.
[思路分析] 本题考查函数极值的逆向应用.(1)根据f(1)=-3-c和f ′(1)=0即可求解;(2)根据函数的导数和单调性的关系可解决.命题方向2 ?已知函数极值求参数典例 2 『规律方法』 已知函数极值,确定函数解析式中的参数时,注意以下两点:
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解.
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.〔跟踪练习2〕
已知函数f(x)=x3-3ax2+2bx在点x=1处的极小值为-1,试确定a、b的值,并求f(x)的单调区间. 右图是函数y=f(x)的导函数y=f ′(x)的图像,对此图像,有如下结论:
①在区间(-2,1)内f(x)是增函数;
②在区间(1,3)内f(x)是减函数;
③x=2时,f(x)取到极大值;
④在x=3时,f(x)取到极小值.
其中正确的是__________(将你认为正确的序号填在横线上).
[思路分析] 给出了y=f ′(x)的图像,应观察图像找出使f ′(x)>0与f ′(x)<0的x的取值范围,并区分f ′(x)的符号由正到负和由负到正,再做判断.命题方向3 ?图像信息问题③ 典例 3 『规律方法』 有关给出图像研究函数性质的题目,要分清给的是f(x)的图像还是f ′(x)的图像,若给的是f(x)的图像,应先找出f(x)的单调区间及极(最)值点,如果给的是f ′(x)的图像,应先找出f ′(x)的正负区间及由正变负还是由负变正,然后结合题目特点分析求解.〔跟踪练习3〕
函数f(x)的定义域为R,导函数f ′(x)的图像如图所示,则函数f(x)( )
A.无极大值点、有四个极小值点
B.有一个极大值点、两个极小值点
C.有两个极大值点、两个极小值点
D.有四个极大值点、无极小值点
[解析] 设f ′(x)与x轴的4个交点,从左至右依次为x1、x2、x3、x4,
当x0,f(x)为增函数,
当x1则x=x1为极大值点,
同理,x=x3为极大值点,x=x2,x=x4为极小值点.C命题方向4 ?分类讨论思想在含参数的函数极值中的应用典例 3 『规律方法』 利用导数求极值时,要先讨论函数的单调性,涉及参数时,必须对参数的取值范围进行讨论(可从导数值为0的几个x值的大小入手).其次,这类问题可以归结为求含参函数的单调性.单调性求出后,极值即可确定.〔跟踪练习4〕
(2019·日照高二检测)已知函数f(x)=x3+ax2+bx+a2在x=1处有极值10,求常数a,b的值.对于方程f(x)=a的根的个数问题,我们可将问题转化为函数y=f(x)与函数y=a的图像的交点个数问题.在解决问题时,可遵循以下步骤:
第一步:利用导数判断函数y=f(x)的单调性及极值等情况,综合各种信息画出函数y=f(x)的大致图像;
第二步:研究函数y=f(x)与y=a的图像的交点个数;
第三步:根据交点个数写出方程根的情况.
如果方程f(x)=0是三次方程,也可以按照如下步骤处理:利用函数极值研究方程根的个数第一步:求导数y=f ′(x),解不等式f ′(x)>0和f ′(x)<0,确定函数的单调性及极值的情况,进一步得到反映三次函数大致趋势的图;
第二步:由趋势图结合交点个数或根的个数写不等式(组),主要看极大值和极小值与0的关系;
第三步:解不等式(组)即可.典例 5 〔跟踪练习5〕
(2019·全国Ⅱ卷文,21)已知函数f(x)=(x-1)ln x-x-1.证明:
(1)f(x)存在唯一的极值点;
(2)f(x)=0有且仅有两个实根,且两个实根互为倒数.注意极大值点与极小值点的区别典例 6 [正解] (在上述解法之后继续)当a=1,b=3时,f ′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去;
当a=2,b=9时,f ′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈[-3,-1]时,f(x)为减函数;当x∈[-1,+∞)时,f(x)为增函数,
所以f(x)在x=-1时取得极小值.因此a=2,b=9.1.函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于( )
A.2 B.3
C.4 D.5D2.函数f(x)在x=x0处导数存在,若p:f ′(x0)=0;q:x=x0是f(x)的极值点,则( )
A.p是q的充分必要条件
B.p是q的充分条件,但不是q的必要条件
C.p是q的必要条件,但不是q的充分条件
D.p既不是q的充分条件,也不是q的必要条件C-2 -19
函数的极值与导数的关系(1)如图是函数y=f(x)的图像,在x=a邻近的左侧f(x)单调递__________,f ′(x)__________0,右侧f(x)单调递__________,_f ′(x)__________0,在x=a邻近的函数值都比f(a)小,且f ′(a)__________0.在x=b邻近情形恰好相反,图形上与a类似的点还有__________,(e,f(e)),与b类似的点还有__________.
我们把点a叫作函数f(x)的极__________值点,f(a)是函数的一个极__________值;把点b叫作函数f(x)的极__________值点,f(b)是函数的一个极__________值.增 > 减 < = (c,_f(c)) (d,f(d)) 大 大 小 小 (2)一般地,已知函数y=f(x)及其定义域内一点x0,对于包含x0在内的开区间(a,b)内的所有点x,如果都有_____________,则称函数f(x)在点x0处取得__________,并把x0称为函数f(x)的一个______________;如果都有__________,则称函数f(x)在点x0处取得__________,并把x0称为函数f(x)的一个__________.极大值与极小值统称为__________,极大值点与极小值点统称为__________.f(x)
2.极值是一个局部性概念,只要在一个小区域内成立即可,要注意极值必须在区间内的连续点取得,一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值也可能大于另一点的极大值,也就是说极大值与极小值没有必然的大小关系.即极大值不一定比极小值大,极小值也不一定比极大值小.(如图)3.若f(x)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在区间上单调的函数没有极值. 1.函数y=x3+1的极大值是( )
A.1 B.0
C.2 D.不存在
[解析] ∵y′=3x2≥0在R上恒成立,
∴函数y=x3+1在R上是单调增函数,
∴函数y=x3+1无极值.D2.下列说法正确的是( )
A.函数在闭区间上的极大值一定比极小值大
B.函数在闭区间上的极大值一定比极小值小
C.函数f(x)=|x|只有一个极小值
D.函数y=f(x)在区间(a,b)上一定存在极值
[解析] 函数的极大值与极小值之间无确定的大小关系,单调函数在区间(a,b)上没有极值,故A,B,D错误,C正确,函数f(x)=|x|只有一个极小值为0.C3.函数f(x)的定义域为开区间(a,b),导函数f ′(x)在(a,b)内的图像如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
A.1个
B.2个
C.3个
D.4个A5.已知k为实数, f(x)=(x2-4)(x+k).
(1)求导函数f ′(x);
(2)若x=-1是函数f(x)的极值点,求y=f(x)在区间[-2,2]上的极值.互动探究学案 求函数y=3x3-x+1的极值.
[思路分析] 首先对函数求导,然后求方程y′=0的根,再检查y′在方程根左右的值的符号.如果左正右负,那么y在这个根处取得极大值;如果左负右正,那么y在这个根处取得极小值.命题方向1 ?利用导数求函数的极值典例 1 『规律方法』 1.当函数f(x)在点x0处连续时,判断f(x0)是否为极大(小)值的方法是:
(1)如果在x0附近的左侧f ′(x)>0,右侧f ′(x)<0,那么f(x0)是极大值;
(2)如果在x0附近的左侧f ′(x)<0,右侧f ′(x)>0,那么f(x0)是极小值;
(3)如果f ′(x)在点x0的左、右两侧符号不变,则f(x0)不是函数f(x)的极值.
2.利用导数求函数极值的步骤:
(1)确定函数的定义域.
(2)求导数f ′(x).
(3)解方程f ′(x)=0得方程的根.
(4)利用方程f ′(x)=0的根将定义域分成若干个小开区间,列表,判定导函数在各个小开区间的符号.
〔跟踪练习1〕
设函数f(x)=x3+ax2-9x的导函数为f ′(x),且f ′(2)=15.
(1)求函数f(x)的图像在x=0处的切线方程;
(2)求函数f(x)的极值.
[解析] (1)∵f ′(x)=3x2+2ax-9,
∵f ′(2)=15,∴12+4a-9=15,∴a=3.
∴f(x)=x3+3x2-9x,
∴f ′(x)=3x2+6x-9,
∴f(0)=0,f ′(0)=-9,
∴函数在x=0处的切线方程为y=-9x. 已知函数f(x)=ax4·ln x+bx4-c(x>0).在x=1处取得极值-3-c,其中a、b为常数.
(1)试确定a、b的值;
(2)讨论函数f(x)的单调区间.
[思路分析] 本题考查函数极值的逆向应用.(1)根据f(1)=-3-c和f ′(1)=0即可求解;(2)根据函数的导数和单调性的关系可解决.命题方向2 ?已知函数极值求参数典例 2 『规律方法』 已知函数极值,确定函数解析式中的参数时,注意以下两点:
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解.
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.〔跟踪练习2〕
已知函数f(x)=x3-3ax2+2bx在点x=1处的极小值为-1,试确定a、b的值,并求f(x)的单调区间. 右图是函数y=f(x)的导函数y=f ′(x)的图像,对此图像,有如下结论:
①在区间(-2,1)内f(x)是增函数;
②在区间(1,3)内f(x)是减函数;
③x=2时,f(x)取到极大值;
④在x=3时,f(x)取到极小值.
其中正确的是__________(将你认为正确的序号填在横线上).
[思路分析] 给出了y=f ′(x)的图像,应观察图像找出使f ′(x)>0与f ′(x)<0的x的取值范围,并区分f ′(x)的符号由正到负和由负到正,再做判断.命题方向3 ?图像信息问题③ 典例 3 『规律方法』 有关给出图像研究函数性质的题目,要分清给的是f(x)的图像还是f ′(x)的图像,若给的是f(x)的图像,应先找出f(x)的单调区间及极(最)值点,如果给的是f ′(x)的图像,应先找出f ′(x)的正负区间及由正变负还是由负变正,然后结合题目特点分析求解.〔跟踪练习3〕
函数f(x)的定义域为R,导函数f ′(x)的图像如图所示,则函数f(x)( )
A.无极大值点、有四个极小值点
B.有一个极大值点、两个极小值点
C.有两个极大值点、两个极小值点
D.有四个极大值点、无极小值点
[解析] 设f ′(x)与x轴的4个交点,从左至右依次为x1、x2、x3、x4,
当x
当x1
同理,x=x3为极大值点,x=x2,x=x4为极小值点.C命题方向4 ?分类讨论思想在含参数的函数极值中的应用典例 3 『规律方法』 利用导数求极值时,要先讨论函数的单调性,涉及参数时,必须对参数的取值范围进行讨论(可从导数值为0的几个x值的大小入手).其次,这类问题可以归结为求含参函数的单调性.单调性求出后,极值即可确定.〔跟踪练习4〕
(2019·日照高二检测)已知函数f(x)=x3+ax2+bx+a2在x=1处有极值10,求常数a,b的值.对于方程f(x)=a的根的个数问题,我们可将问题转化为函数y=f(x)与函数y=a的图像的交点个数问题.在解决问题时,可遵循以下步骤:
第一步:利用导数判断函数y=f(x)的单调性及极值等情况,综合各种信息画出函数y=f(x)的大致图像;
第二步:研究函数y=f(x)与y=a的图像的交点个数;
第三步:根据交点个数写出方程根的情况.
如果方程f(x)=0是三次方程,也可以按照如下步骤处理:利用函数极值研究方程根的个数第一步:求导数y=f ′(x),解不等式f ′(x)>0和f ′(x)<0,确定函数的单调性及极值的情况,进一步得到反映三次函数大致趋势的图;
第二步:由趋势图结合交点个数或根的个数写不等式(组),主要看极大值和极小值与0的关系;
第三步:解不等式(组)即可.典例 5 〔跟踪练习5〕
(2019·全国Ⅱ卷文,21)已知函数f(x)=(x-1)ln x-x-1.证明:
(1)f(x)存在唯一的极值点;
(2)f(x)=0有且仅有两个实根,且两个实根互为倒数.注意极大值点与极小值点的区别典例 6 [正解] (在上述解法之后继续)当a=1,b=3时,f ′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去;
当a=2,b=9时,f ′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈[-3,-1]时,f(x)为减函数;当x∈[-1,+∞)时,f(x)为增函数,
所以f(x)在x=-1时取得极小值.因此a=2,b=9.1.函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于( )
A.2 B.3
C.4 D.5D2.函数f(x)在x=x0处导数存在,若p:f ′(x0)=0;q:x=x0是f(x)的极值点,则( )
A.p是q的充分必要条件
B.p是q的充分条件,但不是q的必要条件
C.p是q的必要条件,但不是q的充分条件
D.p既不是q的充分条件,也不是q的必要条件C-2 -19
同课章节目录
