第二十章 数据的分析单元测试卷(解析版)
图片预览



文档简介
2019-2020人教版八年级数学下册第20章数据的分析单元卷解析版
一、选择题(每小题3分,共30分)
1.某市6月份某周气温(单位:℃)为23、25、28、25、28、31、28,则这组数据的众数和中位数分别是(??? )
A.?25、25???????????????????????????????B.?28、28???????????????????????????????C.?25、28???????????????????????????????D.?28、31
2.已知一组数据共有 个数,前面 个数的平均数是 ,后面 个数的平均数是 ,则这 个数的平均数是(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
3.下表为某校八年级72位女生在规定时间内的立定投篮数统计,
投进的个数
5
6
7
8
9
10
11
12
13
14
15
人数
3
7
6
10
11
8
13
7
1
4
2
若投篮投进个数的中位数为 ,众数为 ,则a+b的值为(?? )
A.?20?????????????????????????????????????????B.?21?????????????????????????????????????????C.?22?????????????????????????????????????????D.?23
4.甲、乙、丙、丁四位同学在一次数学测验中的平均成绩是90分,而甲、乙、丙三人的平均成绩是88分,下列说法一定正确的是( )
A.?丁同学的成绩比其他三个同学的成绩都好???????B.?四位同学成绩的中位数一定是其中一位同学的成绩 C.?四位同学成绩的众数一定是90分?????????????????????D.?丁同学成绩是96分
5.某校男子篮球队20名队员的身高如表所示:则此男子排球队20名队员身高的中位数是(?? )
身高(cm)
170
176
178
182
198
人数(个)
4
6
5
3
2
A.?176cm???????????????????????????????B.?177cm???????????????????????????????C.?178cm???????????????????????????????D.?180cm
6.甲,乙,丙,丁四名同学在学校演讲选拔赛的成绩平均数 与方差s2如下表所示:
甲
乙
丙
丁
平均数
8.0
8.0
8.5
8.5
方差s2
3.5
15.5
3.5
16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择(??? )
A.?甲?????????????????????????????????????????B.?乙?????????????????????????????????????????C.?丙?????????????????????????????????????????D.?丁
7.已知一组数据 ,平均数为2,方差为3,那么另一组数 的平均数和方差分别是(?? )
A.?2, ??????????????????????????????????B.?3,3??????????????????????????????????C.?3,12??????????????????????????????????D.?3,4
8.某市一周日最高气温如图所示,则该市这周的日最高气温的众数是(? ?)
A.?25?????????????????????????????????????????B.?26?????????????????????????????????????????C.?27?????????????????????????????????????????D.?28
9.点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是(???? )
A.?平均数????????????????????????????????B.?中位数?????????????????????????????????C.?方差?????????????????????????????????D.?标准差
10.如表记录了两位射击运动员的八次训练成绩:
次数环数
运动员
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
甲
10
7
7
8
8
8
9
7
乙
10
5
5
8
9
9
8
10
根据以上数据,设甲、乙的平均数分别为 、 ,甲、乙的方差分别为 , ,则下列结论正确的是(??? )
A.? , B.? , C.? , D.? ,
二、填空题(每小题3分,共18分)
11.某招聘考试分笔试和面试两种,小明笔试成绩90分,面试成绩85分,如果笔试成绩、面试成绩按3:2计算,那么小明的平均成绩是________分
12.已知一组数据2、7、9、10、x的平均数与众数相等,则x的值为________.
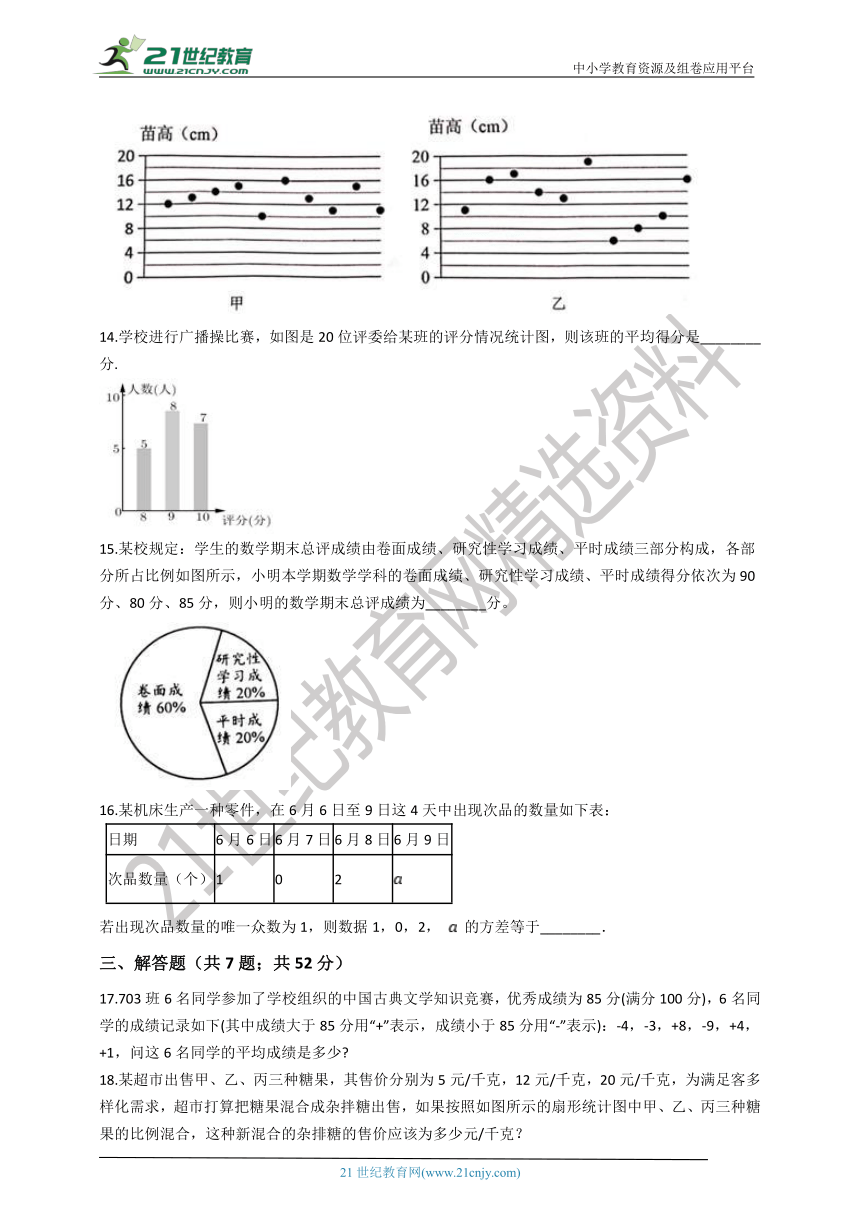
13.为了考察甲、乙两块地小麦的长势,分别从中随机抽出10株苗,测得苗高如图所示.若 和 分别表示甲、乙两块地苗高数据的方差,则 ________ .(填“>”、“<”或“=”).
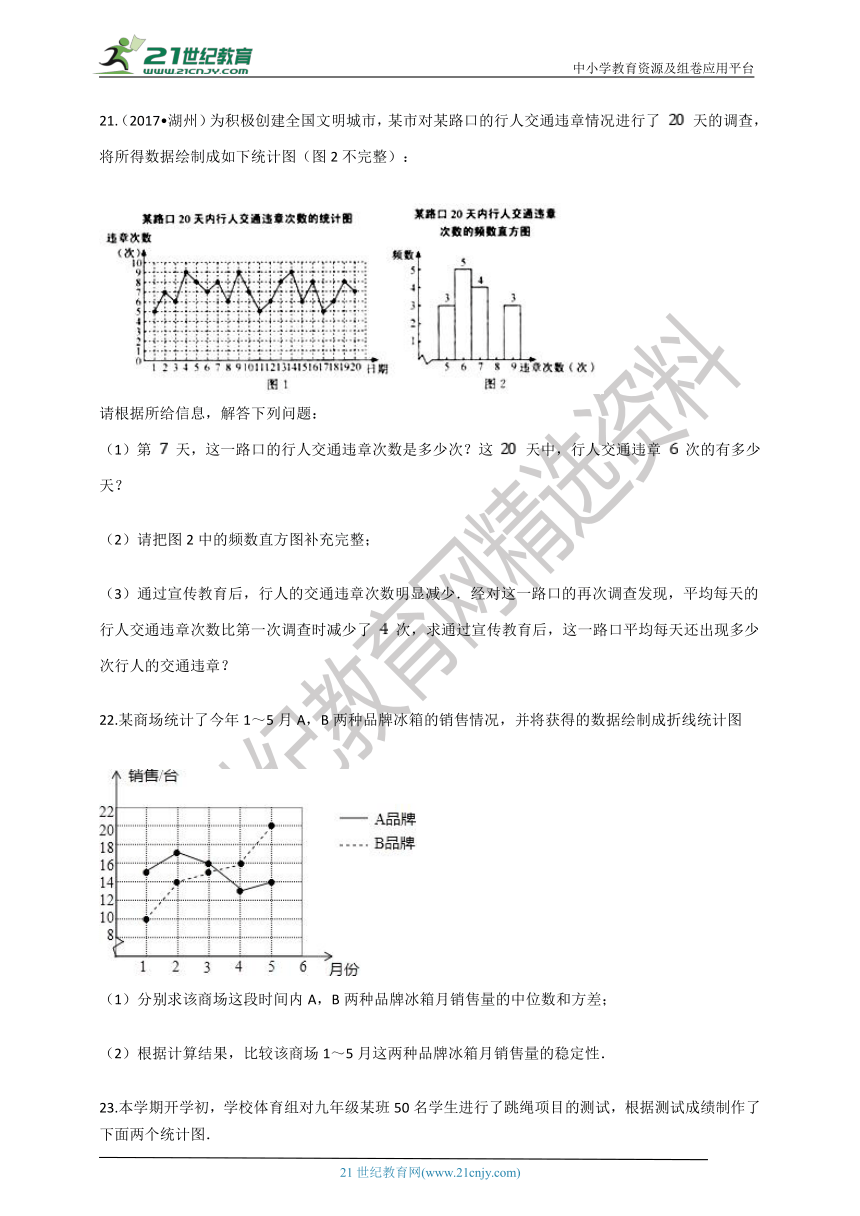
14.学校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班的平均得分是________分.
15.某校规定:学生的数学期末总评成绩由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示,小明本学期数学学科的卷面成绩、研究性学习成绩、平时成绩得分依次为90分、80分、85分,则小明的数学期末总评成绩为________分。
16.某机床生产一种零件,在6月6日至9日这4天中出现次品的数量如下表:
日期
6月6日
6月7日
6月8日
6月9日
次品数量(个)
1
0
2
若出现次品数量的唯一众数为1,则数据1,0,2, 的方差等于________.
三、解答题(共7题;共52分)
17.703班6名同学参加了学校组织的中国古典文学知识竞赛,优秀成绩为85分(满分100分),6名同学的成绩记录如下(其中成绩大于85分用“+”表示,成绩小于85分用“-”表示):-4,-3,+8,-9,+4,+1,问这6名同学的平均成绩是多少?
18.某超市出售甲、乙、丙三种糖果,其售价分别为5元/千克,12元/千克,20元/千克,为满足客多样化需求,超市打算把糖果混合成杂拌糖出售,如果按照如图所示的扇形统计图中甲、乙、丙三种糖果的比例混合,这种新混合的杂排糖的售价应该为多少元/千克?
19.某中学开展演讲比赛活动,八年级(1)班、八年级(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分100分)如下图:八年级(1)班成绩为条形统计图,八年级(2)班成绩为扇形统计图.
(1)根据上图填写下表
班别
平均数(分)
中位数(分)
众数(分)
八年级(1)班
85
________
85
八年级(2)班
85
80
________
(2)如果要在复赛成绩的十名选手中决定在同一班中选五名参加比赛活动,你认为哪个班实力更强一些?通过计算,说明理由.
20.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项: A.1.5小时以上??? B.1~1.5小时??? C.0.5~1小时? D.0.5小时以下 图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了________名学生;学生参加体育活动时间的中位数落在________时间段(填写上面所给“A”、“B”、“C”、“D”中的一个选项);
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
21.(2017?湖州)为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了 天的调查,将所得数据绘制成如下统计图(图2不完整):
请根据所给信息,解答下列问题:
(1)第 天,这一路口的行人交通违章次数是多少次?这 天中,行人交通违章 次的有多少天?
(2)请把图2中的频数直方图补充完整;
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
22.某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
23.本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
2019-2020人教版八年级数学下册第20章数据的分析单元卷解析版
一、选择题
1.解:将这组数据按从小到大的顺序排列23,25,25,28,28,28,31,
在这一组数据中28是出现次数最多的,故众数是28℃.
处于中间位置的那个数是28,那么由中位数的定义可知,这组数据的中位数是28℃;
故答案为:B.
2.解:由题意得:(10×14+15×6)÷20=11.5,
故答案为:C.
3.第36 与37人投中的个数均为9,故中位数a=9,
11出现了13次,次数最多,故众数b=11,
所以a+b=9+11=20.
故答案为:A.
4.解:A、丁同学的成绩为90×4﹣88×3=96(分),而由甲、乙、丙三人的平均成绩是88分无法判断三人的具体成绩,无法比较,此选项不符合题意;
B、四位同学成绩的中位数可能是四个数据中的一个,也可能不在所列数据中,此选项不符合题意;
C、由于不清楚四位同学的各自成绩,所以不能判断众数,此选项不符合题意;
D、丁同学的成绩为90×4﹣88×3=96(分),此选项符合题意;
故答案为:D .
5.解:表格中第10,11位队员的身高分别为176cm、178cm,
故中位数为 cm,
故答案为:B.
6.解:丙丁平均成绩较高为8.5, 但丙的方差较小,成绩发挥稳定,应选丁. 故答案为:C. 7.解: =2×2-1=3; =4×3=12. 故答案为:C. 8.解:∵25出现了3次,出现的次数最多,
∴周的日最高气温的众数是25.
故答案为:A.
9.解:依题可得,
这组数据的中位数为: =41,
∴计算结果与被涂污数字无关的是中位数.
故答案为:B.
10.解: ; ;
; ,
∴ , ,
故答案为:A.
二、填空题
11.解: 根据题意,小明的平均成绩是 (分), 故答案为:88.
12.∵数据2、7、9、10、x的平均数与众数相等,
∴ =x ,
∴x=7.
故填7.
13.解:由图可知,甲、乙两块地的苗高皆在12cm上下波动,但乙的波动幅度比甲大,
∴ 则??< 14.解:依题可得,
该班的平均分为: =9.1.
故答案为:9.1.
15解:由题意得 90×60%+80×20%+85×20%=87. 故答案为:87
16.解:∵出现次品数量的唯一众数为1,
∴ ,
∴ ,
∴ ,
故答案为 .
三、解答题
17. 解:由已知可得这6名同学的成绩为81,82,93,76,89,86,
(81+82+93+76+89+86)÷6
=84.5
答:这6名同学的平均成绩是84.5分。
18. 解:丙对应的百分比为1-50%-30%=20%
∴这种新混合物的杂拌糖的售价应该为5×50%+12×30%+20×20%=10.1(元/千克)
答:这种新混合的杂排糖的售价应该为10.1元/千克.
19.(1)85;100 (2)② = ×[(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70,
= ×[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160,
∵八年级(1)班的方差小于八年级(2)班的方差,
所以选派八年级(1)班参加比赛.
解:(1)将八年级(1)班成绩重新排列为75、80、85、85、100,
∴其中位数为85分,
八年级(2)班100分人数最多,
所以其众数为100,
补全表格如下:
班别
平均数(分)
中位数(分)
众数(分)
八年级(1)班
85
85
85
八年级(2)班
85
80
100
20.(1)200;B (2)解:“B”有200?60?30?10=100人,补全统计图如图所示: (3)解:用样本估计总体,每天参加体育锻炼在0.5小时以下占5%;则3000×5%=150, 学校有150人平均每天参加体育锻炼在0.5小时以下.
解:(1)读图可得:A类有60人,占30%;则本次一共调查了60÷30%=200人;本次一共调查了200位学生;学生参加体育活动时间的中位数落在B时间段. 21. (1)解:依题可得:第7天,这一路口的行人交通违章次数是8次.
? 这20天中,行人交通违章6次的有5天.
(2)解:补全的频数直方图如图所示:
(3)解:第一次调查,平均每天行人的交通违章次数为:
""=7(次).
∵7-4=3(次)
∴通过宣传教育后,这一路口平均每天还出现3次行人的交通违章.
22.(1)解: A品牌冰箱月销售量从小到大的排列为:13,14,15,16,17,
B品牌冰箱月销售量从小到大排列为:10,14,15,16,20,
∴A品牌冰箱月销售量的中位数为15台,B品牌冰箱月销售量的中位数为15台,
∵ = =15(台); = =15(台),
则SA2= =2,SB2= =10.4
(2)∵SA2<SB2 ,
∴A品牌冰箱的月销售量稳定.
23.(1)解:根据题意得:
得4分的学生有50×50%=25(人),
答:得4分的学生有25人
(2)解:根据题意得:
平均分= =3.7(分)
(3)解:设第二次测试中得4分的学生有x人,得5分的学生有y人,根据题意得:
,
解得: ,
答:第二次测试中得4分的学生有15人,得5分的学生有30人
一、选择题(每小题3分,共30分)
1.某市6月份某周气温(单位:℃)为23、25、28、25、28、31、28,则这组数据的众数和中位数分别是(??? )
A.?25、25???????????????????????????????B.?28、28???????????????????????????????C.?25、28???????????????????????????????D.?28、31
2.已知一组数据共有 个数,前面 个数的平均数是 ,后面 个数的平均数是 ,则这 个数的平均数是(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
3.下表为某校八年级72位女生在规定时间内的立定投篮数统计,
投进的个数
5
6
7
8
9
10
11
12
13
14
15
人数
3
7
6
10
11
8
13
7
1
4
2
若投篮投进个数的中位数为 ,众数为 ,则a+b的值为(?? )
A.?20?????????????????????????????????????????B.?21?????????????????????????????????????????C.?22?????????????????????????????????????????D.?23
4.甲、乙、丙、丁四位同学在一次数学测验中的平均成绩是90分,而甲、乙、丙三人的平均成绩是88分,下列说法一定正确的是( )
A.?丁同学的成绩比其他三个同学的成绩都好???????B.?四位同学成绩的中位数一定是其中一位同学的成绩 C.?四位同学成绩的众数一定是90分?????????????????????D.?丁同学成绩是96分
5.某校男子篮球队20名队员的身高如表所示:则此男子排球队20名队员身高的中位数是(?? )
身高(cm)
170
176
178
182
198
人数(个)
4
6
5
3
2
A.?176cm???????????????????????????????B.?177cm???????????????????????????????C.?178cm???????????????????????????????D.?180cm
6.甲,乙,丙,丁四名同学在学校演讲选拔赛的成绩平均数 与方差s2如下表所示:
甲
乙
丙
丁
平均数
8.0
8.0
8.5
8.5
方差s2
3.5
15.5
3.5
16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择(??? )
A.?甲?????????????????????????????????????????B.?乙?????????????????????????????????????????C.?丙?????????????????????????????????????????D.?丁
7.已知一组数据 ,平均数为2,方差为3,那么另一组数 的平均数和方差分别是(?? )
A.?2, ??????????????????????????????????B.?3,3??????????????????????????????????C.?3,12??????????????????????????????????D.?3,4
8.某市一周日最高气温如图所示,则该市这周的日最高气温的众数是(? ?)
A.?25?????????????????????????????????????????B.?26?????????????????????????????????????????C.?27?????????????????????????????????????????D.?28
9.点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是(???? )
A.?平均数????????????????????????????????B.?中位数?????????????????????????????????C.?方差?????????????????????????????????D.?标准差
10.如表记录了两位射击运动员的八次训练成绩:
次数环数
运动员
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
甲
10
7
7
8
8
8
9
7
乙
10
5
5
8
9
9
8
10
根据以上数据,设甲、乙的平均数分别为 、 ,甲、乙的方差分别为 , ,则下列结论正确的是(??? )
A.? , B.? , C.? , D.? ,
二、填空题(每小题3分,共18分)
11.某招聘考试分笔试和面试两种,小明笔试成绩90分,面试成绩85分,如果笔试成绩、面试成绩按3:2计算,那么小明的平均成绩是________分
12.已知一组数据2、7、9、10、x的平均数与众数相等,则x的值为________.
13.为了考察甲、乙两块地小麦的长势,分别从中随机抽出10株苗,测得苗高如图所示.若 和 分别表示甲、乙两块地苗高数据的方差,则 ________ .(填“>”、“<”或“=”).
14.学校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班的平均得分是________分.
15.某校规定:学生的数学期末总评成绩由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示,小明本学期数学学科的卷面成绩、研究性学习成绩、平时成绩得分依次为90分、80分、85分,则小明的数学期末总评成绩为________分。
16.某机床生产一种零件,在6月6日至9日这4天中出现次品的数量如下表:
日期
6月6日
6月7日
6月8日
6月9日
次品数量(个)
1
0
2
若出现次品数量的唯一众数为1,则数据1,0,2, 的方差等于________.
三、解答题(共7题;共52分)
17.703班6名同学参加了学校组织的中国古典文学知识竞赛,优秀成绩为85分(满分100分),6名同学的成绩记录如下(其中成绩大于85分用“+”表示,成绩小于85分用“-”表示):-4,-3,+8,-9,+4,+1,问这6名同学的平均成绩是多少?
18.某超市出售甲、乙、丙三种糖果,其售价分别为5元/千克,12元/千克,20元/千克,为满足客多样化需求,超市打算把糖果混合成杂拌糖出售,如果按照如图所示的扇形统计图中甲、乙、丙三种糖果的比例混合,这种新混合的杂排糖的售价应该为多少元/千克?
19.某中学开展演讲比赛活动,八年级(1)班、八年级(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分100分)如下图:八年级(1)班成绩为条形统计图,八年级(2)班成绩为扇形统计图.
(1)根据上图填写下表
班别
平均数(分)
中位数(分)
众数(分)
八年级(1)班
85
________
85
八年级(2)班
85
80
________
(2)如果要在复赛成绩的十名选手中决定在同一班中选五名参加比赛活动,你认为哪个班实力更强一些?通过计算,说明理由.
20.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项: A.1.5小时以上??? B.1~1.5小时??? C.0.5~1小时? D.0.5小时以下 图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了________名学生;学生参加体育活动时间的中位数落在________时间段(填写上面所给“A”、“B”、“C”、“D”中的一个选项);
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
21.(2017?湖州)为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了 天的调查,将所得数据绘制成如下统计图(图2不完整):
请根据所给信息,解答下列问题:
(1)第 天,这一路口的行人交通违章次数是多少次?这 天中,行人交通违章 次的有多少天?
(2)请把图2中的频数直方图补充完整;
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
22.某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
23.本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
2019-2020人教版八年级数学下册第20章数据的分析单元卷解析版
一、选择题
1.解:将这组数据按从小到大的顺序排列23,25,25,28,28,28,31,
在这一组数据中28是出现次数最多的,故众数是28℃.
处于中间位置的那个数是28,那么由中位数的定义可知,这组数据的中位数是28℃;
故答案为:B.
2.解:由题意得:(10×14+15×6)÷20=11.5,
故答案为:C.
3.第36 与37人投中的个数均为9,故中位数a=9,
11出现了13次,次数最多,故众数b=11,
所以a+b=9+11=20.
故答案为:A.
4.解:A、丁同学的成绩为90×4﹣88×3=96(分),而由甲、乙、丙三人的平均成绩是88分无法判断三人的具体成绩,无法比较,此选项不符合题意;
B、四位同学成绩的中位数可能是四个数据中的一个,也可能不在所列数据中,此选项不符合题意;
C、由于不清楚四位同学的各自成绩,所以不能判断众数,此选项不符合题意;
D、丁同学的成绩为90×4﹣88×3=96(分),此选项符合题意;
故答案为:D .
5.解:表格中第10,11位队员的身高分别为176cm、178cm,
故中位数为 cm,
故答案为:B.
6.解:丙丁平均成绩较高为8.5, 但丙的方差较小,成绩发挥稳定,应选丁. 故答案为:C. 7.解: =2×2-1=3; =4×3=12. 故答案为:C. 8.解:∵25出现了3次,出现的次数最多,
∴周的日最高气温的众数是25.
故答案为:A.
9.解:依题可得,
这组数据的中位数为: =41,
∴计算结果与被涂污数字无关的是中位数.
故答案为:B.
10.解: ; ;
; ,
∴ , ,
故答案为:A.
二、填空题
11.解: 根据题意,小明的平均成绩是 (分), 故答案为:88.
12.∵数据2、7、9、10、x的平均数与众数相等,
∴ =x ,
∴x=7.
故填7.
13.解:由图可知,甲、乙两块地的苗高皆在12cm上下波动,但乙的波动幅度比甲大,
∴ 则??< 14.解:依题可得,
该班的平均分为: =9.1.
故答案为:9.1.
15解:由题意得 90×60%+80×20%+85×20%=87. 故答案为:87
16.解:∵出现次品数量的唯一众数为1,
∴ ,
∴ ,
∴ ,
故答案为 .
三、解答题
17. 解:由已知可得这6名同学的成绩为81,82,93,76,89,86,
(81+82+93+76+89+86)÷6
=84.5
答:这6名同学的平均成绩是84.5分。
18. 解:丙对应的百分比为1-50%-30%=20%
∴这种新混合物的杂拌糖的售价应该为5×50%+12×30%+20×20%=10.1(元/千克)
答:这种新混合的杂排糖的售价应该为10.1元/千克.
19.(1)85;100 (2)② = ×[(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70,
= ×[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160,
∵八年级(1)班的方差小于八年级(2)班的方差,
所以选派八年级(1)班参加比赛.
解:(1)将八年级(1)班成绩重新排列为75、80、85、85、100,
∴其中位数为85分,
八年级(2)班100分人数最多,
所以其众数为100,
补全表格如下:
班别
平均数(分)
中位数(分)
众数(分)
八年级(1)班
85
85
85
八年级(2)班
85
80
100
20.(1)200;B (2)解:“B”有200?60?30?10=100人,补全统计图如图所示: (3)解:用样本估计总体,每天参加体育锻炼在0.5小时以下占5%;则3000×5%=150, 学校有150人平均每天参加体育锻炼在0.5小时以下.
解:(1)读图可得:A类有60人,占30%;则本次一共调查了60÷30%=200人;本次一共调查了200位学生;学生参加体育活动时间的中位数落在B时间段. 21. (1)解:依题可得:第7天,这一路口的行人交通违章次数是8次.
? 这20天中,行人交通违章6次的有5天.
(2)解:补全的频数直方图如图所示:
(3)解:第一次调查,平均每天行人的交通违章次数为:
""=7(次).
∵7-4=3(次)
∴通过宣传教育后,这一路口平均每天还出现3次行人的交通违章.
22.(1)解: A品牌冰箱月销售量从小到大的排列为:13,14,15,16,17,
B品牌冰箱月销售量从小到大排列为:10,14,15,16,20,
∴A品牌冰箱月销售量的中位数为15台,B品牌冰箱月销售量的中位数为15台,
∵ = =15(台); = =15(台),
则SA2= =2,SB2= =10.4
(2)∵SA2<SB2 ,
∴A品牌冰箱的月销售量稳定.
23.(1)解:根据题意得:
得4分的学生有50×50%=25(人),
答:得4分的学生有25人
(2)解:根据题意得:
平均分= =3.7(分)
(3)解:设第二次测试中得4分的学生有x人,得5分的学生有y人,根据题意得:
,
解得: ,
答:第二次测试中得4分的学生有15人,得5分的学生有30人
