湘教版九年级下册数学 第2章 圆 达标检测卷(含答案)
文档属性
| 名称 | 湘教版九年级下册数学 第2章 圆 达标检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-29 21:12:28 | ||
图片预览


文档简介
湘教版九年级下册数学 第2章 圆 达标检测卷
时间:120分钟 满分:120分
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.⊙O的半径为6cm,点A到圆心O的距离OA=5cm,则点A与⊙O的位置关系是( )
A.点A在⊙O上 B.点A在⊙O内 C.点A在⊙O外 D.无法确定
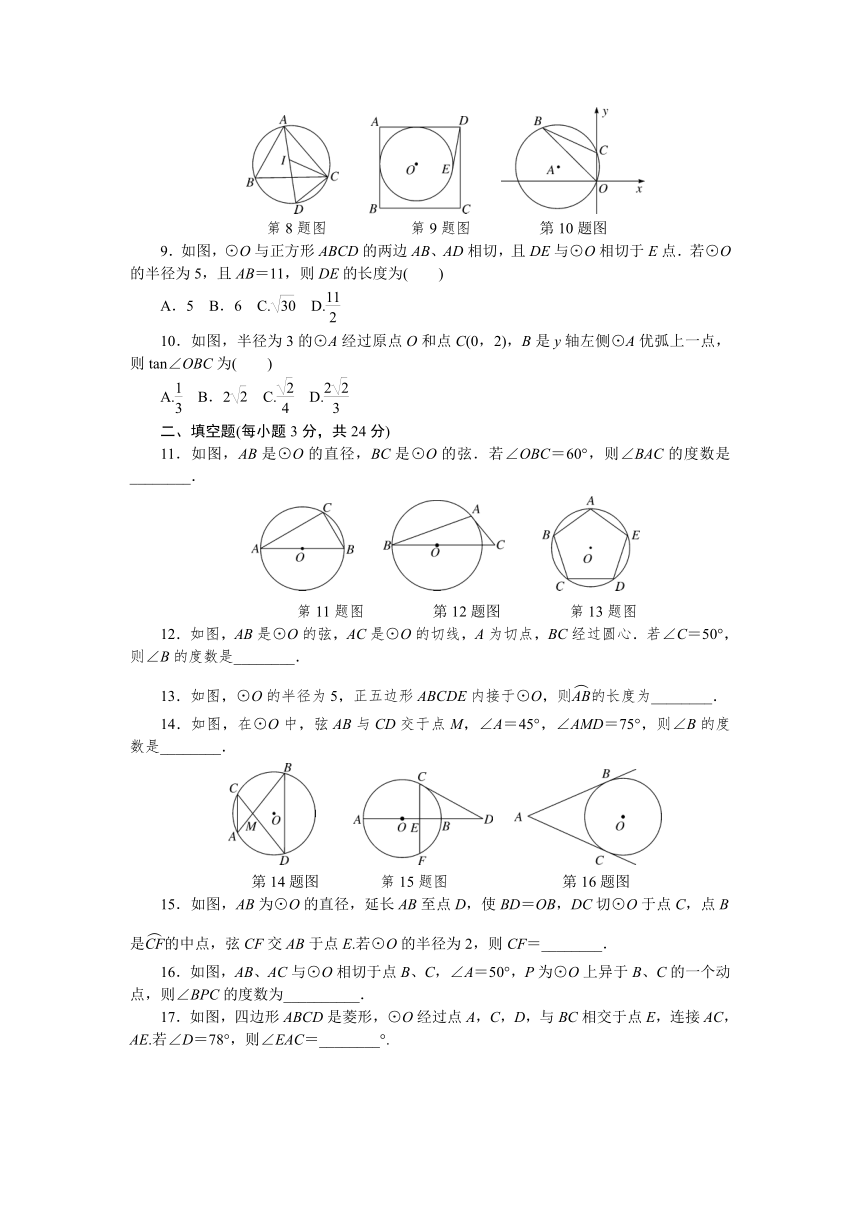
2.如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是( )
A.40° B.30° C.20° D.15°
第2题图 第3题图 第4题图
3.如图,AB是⊙O的直径,已知∠DCB=20°,则∠DBA的度数为( )
A.50° B.20° C.60° D.70°
4.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( )
A.69° B.42° C.48° D.38°
5.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,∠BDC=110°,连接AC,则∠A的度数是( )
A.70° B.45° C.35° D.25°
第5题图 第6题图 第7题图
6.如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )
A.5cm B.8cm C.10cm D.12cm
7.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
A.175πcm2 B.350πcm2 C.πcm2 D.150πcm2
8.如图,在△ABC中,∠ABC=60°,∠ACB=50°,I是△ABC的内心,延长AI交△ABC的外接圆于点D,则∠ICD的度数是( )
A.50° B.55° C.60° D.65°
第8题图 第9题图 第10题图
9.如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若⊙O的半径为5,且AB=11,则DE的长度为( )
A.5 B.6 C. D.
10.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
二、填空题(每小题3分,共24分)
11.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是________.
第11题图 第12题图 第13题图
12.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=50°,则∠B的度数是________.
13.如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则的长度为________.
14.如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是________.
第14题图 第15题图 第16题图
15.如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=________.
16.如图,AB、AC与⊙O相切于点B、C,∠A=50°,P为⊙O上异于B、C的一个动点,则∠BPC的度数为__________.
17.如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=78°,则∠EAC=________°.
第17题图 第18题图
18.如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若半径为1.5cm的⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为____________.
三、解答题(共66分)
19.(6分)如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
20.(8分)如图,在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);
(2)若∠B=60°,AB=3,求⊙P的面积.
21.(8分)如图,AB是半圆O的直径,C,D是半圆O上的两点,OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
22.(10分)如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).
23.(10分)如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,∠CDB=∠OBD=30°,DB=6cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD,BD与弧BC所围成的阴影部分的面积(结果保留π).
24.(10分)如图,已知AB是半径为1的⊙O的直径,C是⊙O上一点,D是BC延长线上一点,过点D的直线交AC于点E,交AB于点F,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=AF,求证:CF⊥AB.
25.(14分)如图所示的图①,②,③,…,,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE……正n边形ABCDE…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
参考答案与解析
1.B 2.C 3.D 4.A 5.C 6.C 7.B
8.C 解析:在△ABC中,∠BAC=180°-∠ABC-∠ACB=180°-60°-50°=70°.∵I是△ABC的内心,∴∠BAD=∠BAC=35°,∠BCI=∠ACB=25°,∴∠BCD=∠BAD=35°,∴∠ICD=∠BCD+∠BCI=35°+25°=60°.故选C.
9.B 解析:设AD切⊙O于点F,AB切⊙O于点G,连接OF,OG.易知四边形AGOF为正方形,∴AF=OF=5,∴DF=AD-AF=AB-AF=11-5=6.∵DE与⊙O相切于E点,∴DE=DF=6.故选B.
10.C 解析:设⊙A与x轴负半轴交于点D,连接CD.∵∠COD=90°,∴CD为⊙A的直径.在Rt△OCD中,CD=6,OC=2,则OD==4,∴tan∠CDO==.由圆周角定理得∠OBC=∠CDO,∴tan∠OBC=tan∠CDO=.故选C.
11.30° 12.20° 13.2π 14.30°
15.2 16.65°或115° 17.27
18.2cm或8cm 解析:分两种情况讨论:如图①,当⊙O平移到⊙O′位置时,⊙O与PA相切时,且切点为C,连接O′C,则O′C⊥PA,即∠O′CP=90°.∵∠APB=30°,O′C=1.5cm,∴O′P=2O′C=3cm.∵OP=5cm,∴OO′=OP-O′P=2(cm).
如图②,当⊙O平移到⊙O′位置时,⊙O与PA相切时,且切点为C,连接O′C,则O′C⊥PA,即∠O′CP=90°.∵∠CPO′=∠APB=30°,O′C=1.5cm,∴O′P=3cm,∴O′O=8cm.综上所述,当⊙O与直线PA相切时,圆心O移动的距离为2cm或8cm.
19.解:在⊙O中,∵∠A=45°,∴∠D=45°.(2分)∵BD为⊙O的直径,∴∠BCD=90°,(4分)∴BC=BD·sin45°=2×=.(6分)
20.
解:(1)如图所示,⊙P为所求作的圆.(4分)
(2)∵∠ABC=60°,BP平分∠ABC,∴∠ABP=30°.∴AP=AB·tan∠ABP=,∴S⊙P=π×()2=3π.(8分)
21.解:(1)∵AB是半圆O的直径,∴∠ACB=90°,∴∠CAB=90°-∠B=90°-70°=20°.∵OD∥BC,∴∠AOD=∠B=70°.(2分)∵OA=OD,∴∠DAO=∠ADO===55°,∴∠CAD=∠DAO-∠CAB=55°-20°=35°.(4分)
(2)在Rt△ABC中,BC===.∵OD∥BC,∴∠AEO=∠ACB=90°,即OE⊥AC,∴AE=EC.又∵OA=OB,∴OE是△ABC的中位线,∴OE=BC=.(7分)又∵OD=AB=2,∴DE=OD-OE=2-.(8分)
22.(1)证明:连接OD.(1分)∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∴∠CFD=∠ODF=90°,∴DF⊥AC.(5分)
(2)解:∵∠CDF=30°,由(1)可知∠ODF=90°,∴∠ODB=180°-∠CDF-∠ODF=60°.∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,(8分)∴l==.(10分)
23.(1)证明:连接OC.(1分)由圆周角定理得∠COB=2∠CDB=2×30°=60°.∵AC∥BD,∴∠A=∠OBD=30°,∴∠OCA=180°-30°-60°=90°,即OC⊥AC.(4分)∵OC为⊙O的半径,∴AC是⊙O的切线.(5分)
(2)解:连接OD.设OC与BD交于点M.由(1)知OC⊥AC.∵AC∥BD,∴OC⊥BD.由垂径定理可知MD=MB=BD=3cm.在Rt△OBM中,∠COB=60°,OB===6(cm).(7分)在△CDM与△OBM中,∵∠CDM=∠OBM=30°,MD=MB,∠CMD=∠OMB=90°,∴△CDM≌△OBM,∴S△CDM=S△OBM,∴S阴影=S扇形BOC==6π(cm2).(10分)
24.证明:(1)∵AB是⊙O的直径,∴∠ACB=90°.∵△AEF为等边三角形,∴∠CAB=∠AFE=60°.又∵∠B+∠CAB=90°,∴∠B=30°.∵∠DFA=∠B+∠BDF=60°,∴∠FDB=30°,则∠FDB=∠B,∴DF=BF,∴△DFB是等腰三角形.(5分)
(2)过点A作AM⊥DF于点M.(6分)设AF=2a,∵△AEF为等边三角形,∴FM=a,AM=a.在Rt△DAM中,AD=AF=2a,AM=a,由勾股定理得DM==5a,∴BF=DF=6a,∴AB=AF+BF=8a.在Rt△ABC中,∠B=30°,∠ACB=90°,∴AC=AB=4a,∴AE=CE=EF=2a,∴∠ECF=∠EFC.∵∠AEF=∠ECF+∠EFC=60°,∴∠CFE=30°,∴∠AFC=∠AFE+∠EFC=60°+30°=90°,即CF⊥AB.(10分)
25.解:(1)连接OA,OB,则OA=OB,∴∠OAB=∠OBM=∠OBN.又BM=CN,∴AM=BN,∴△AOM≌△BON,∴∠AOM=∠BON.又∵∠AOB=×360°=120°,∴∠MON=∠BON+∠MOB=∠AOM+∠MOB=∠AOB=120°.(5分)
(2)90° 72°(11分)
(3)∠MON=.(14分)
