【复习讲义】四年级上册数学试题-第三章《观察物体》(含解析)苏教新版
文档属性
| 名称 | 【复习讲义】四年级上册数学试题-第三章《观察物体》(含解析)苏教新版 |

|
|
| 格式 | zip | ||
| 文件大小 | 429.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-30 00:00:00 | ||
图片预览

文档简介
【复习讲义】2019-2020学年苏教新版四年级上册
第三章:观察物体(提高版)
【学生版】
【知识点总结】
同样的物体,从不同的面看到的图形可能一样,也可能不一样。
无论从哪个角度观察,从一个点最多只能看到物体的三个面。
规则长方体中小正方体个数=层数×一层小正方体个数
不规则长方体中小正方体个数1)层数×每层可视小正方体个数
2)在前面小正方形上标数字
【习题巩固】
一.选择题(共7小题)
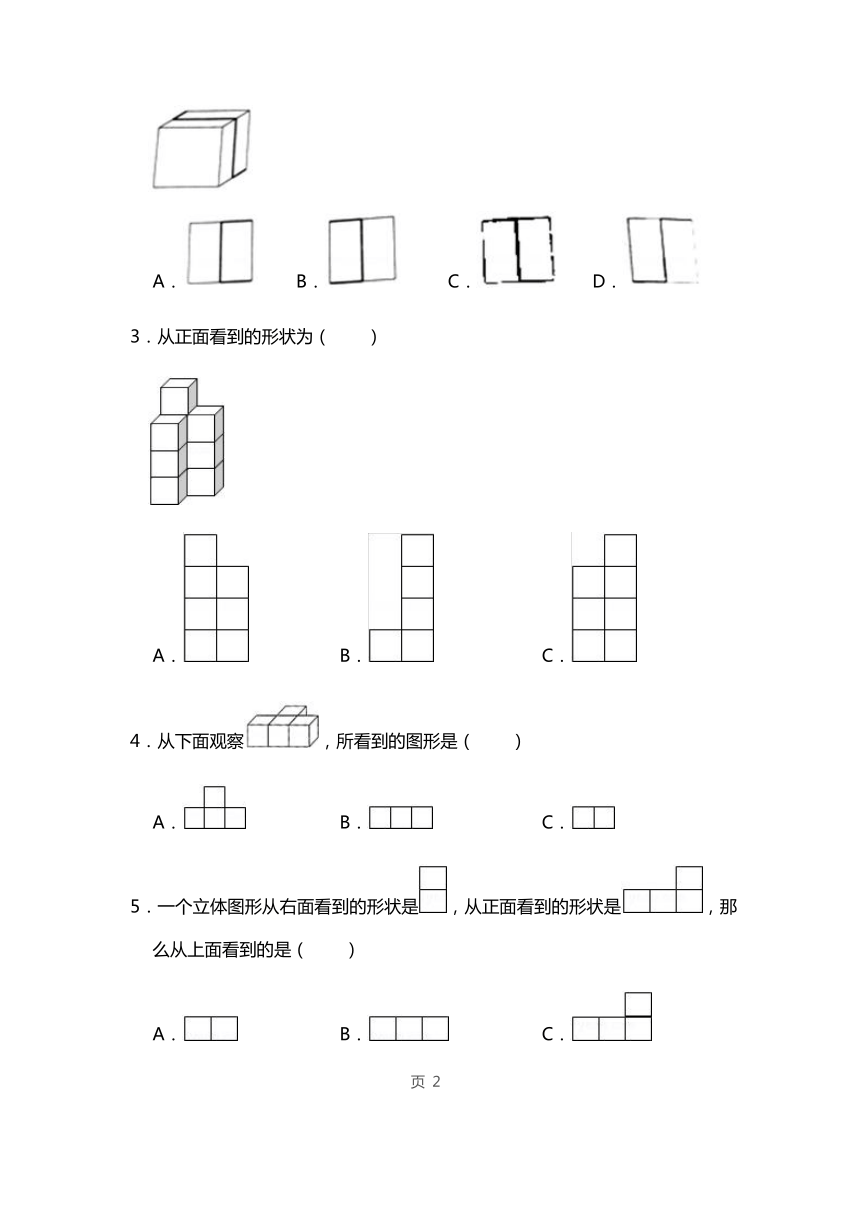
1.如图是由8个小正方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置上的小正方体的个数,则这个几何体从左面看到的是( )
A. B. C. D.
2.如图为一个用玻璃制成的立方体,粗线部分表示一根嵌在正方体内的铁丝.下列选项中( )表示从立方体左面看到的图.
A. B. C. D.
3.从正面看到的形状为( )
A. B. C.
4.从下面观察,所看到的图形是( )
A. B. C.
5.一个立体图形从右面看到的形状是,从正面看到的形状是,那么从上面看到的是( )
A. B. C.
6.是由5个小正方体组成的平面图形,下面图形( )是从上面观察到的.
A. B.
C.
7.从正面看图中的物体,看到的是什么图形?( )
A. B.
C.
二.填空题(共7小题)
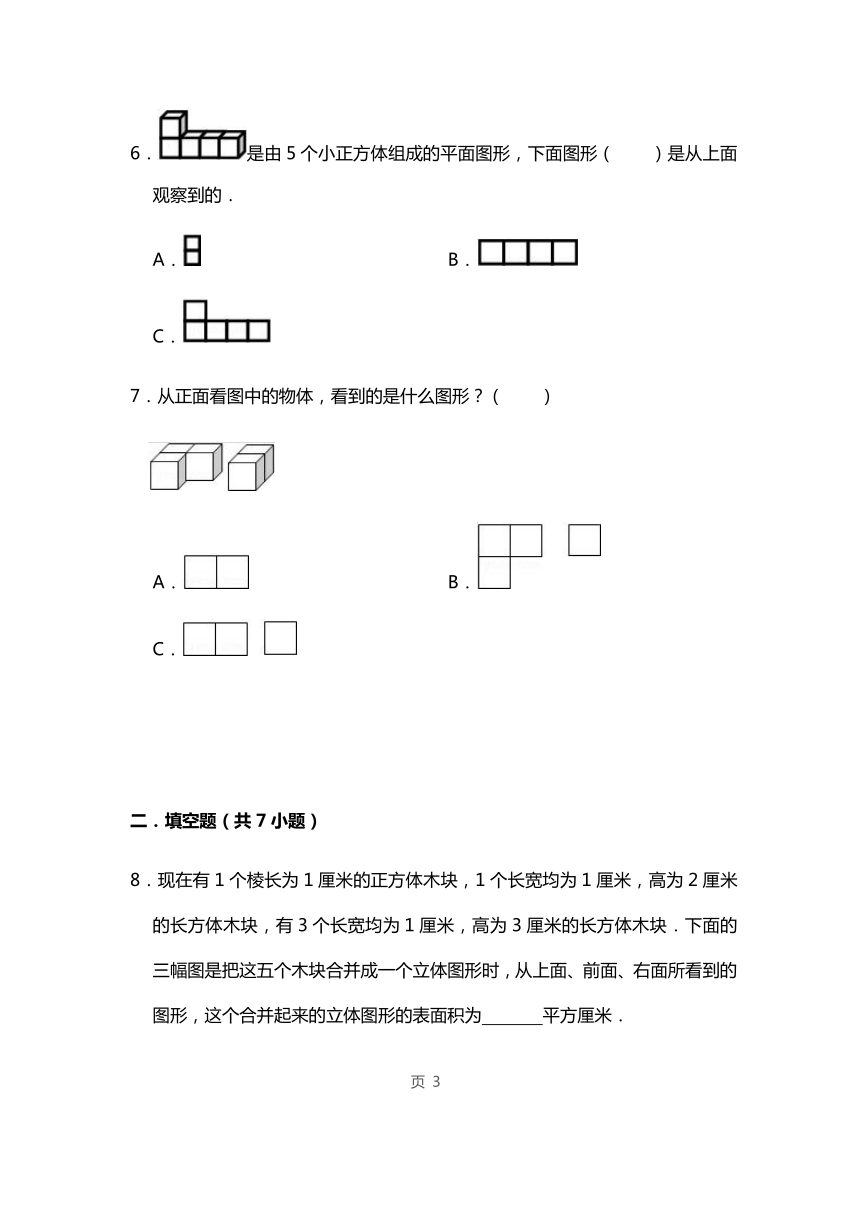
8.现在有1个棱长为1厘米的正方体木块,1个长宽均为1厘米,高为2厘米的长方体木块,有3个长宽均为1厘米,高为3厘米的长方体木块.下面的三幅图是把这五个木块合并成一个立体图形时,从上面、前面、右面所看到的图形,这个合并起来的立体图形的表面积为 平方厘米.
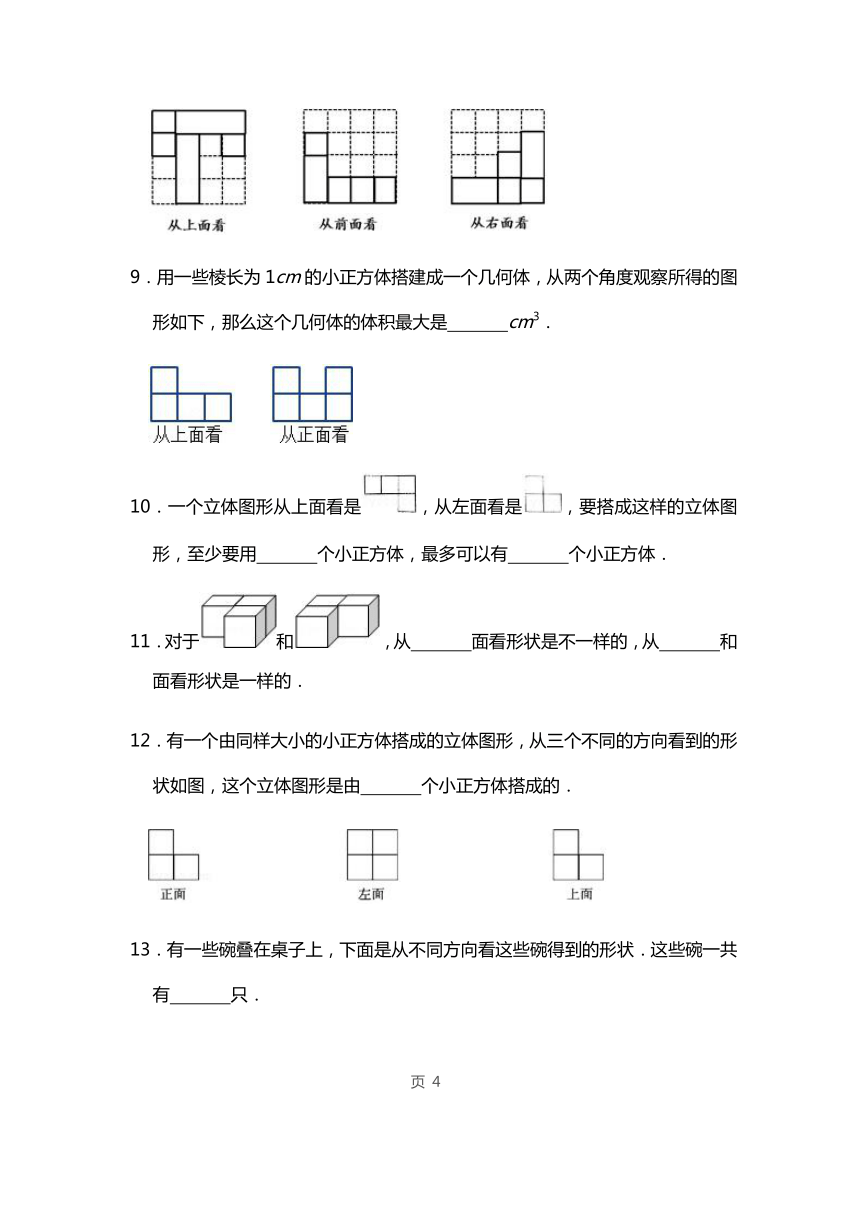
9.用一些棱长为1cm的小正方体搭建成一个几何体,从两个角度观察所得的图形如下,那么这个几何体的体积最大是 cm3.
10.一个立体图形从上面看是,从左面看是,要搭成这样的立体图形,至少要用 个小正方体,最多可以有 个小正方体.
11.对于和,从 面看形状是不一样的,从 和 面看形状是一样的.
12.有一个由同样大小的小正方体搭成的立体图形,从三个不同的方向看到的形状如图,这个立体图形是由 个小正方体搭成的.
13.有一些碗叠在桌子上,下面是从不同方向看这些碗得到的形状.这些碗一共有 只.
14.一个用小正方体搭成的几何体,下面是从它的两个不同方向看到的形状,要符合这两个条件,最少需要摆 块,最多能摆 块.
三.判断题(共4小题)
15.一个同学从正面、左面、后面观察到的房子如图.下面说法正确的画“√”,错误的画“?”.
(1)这座房子有三扇窗户和一扇门. (判断对错)
(2)这座房子的窗户都在它的正面. (判断对错)
(3)这座房子后边有一扇窗户. (判断对错)
16.不同的物体分别从不同的角度观察,看到的现状有可能是相同的. (判断对错)
17.一个立体图形,从上面看到的形状是,从正面看到的形状是.搭这样的一个立体图形,至少需要4个小立方块. .(判断对错)
18.一个物体由于观察的角度不同看到的形状一定也不相同. .(判断对错)
四.操作题(共5小题)
19.如图是用5个小正方体搭成的立体图形,分别画出从上面、正面和左面看到的形状.
20.画出下列图形从前面、上面、左面看到的形状.
21.分别画出从正面、上面、侧面观察下面物体时看到的形状.
正面看到的形状是:
上面看到的形状是:
侧面看到的形状是:
22.如图的物体从上面、前面、右面看到的形状分别是什么?请在方格纸上画出来.
23.根据下面从不同方向看到的图形摆一摆.
在摆法正确的下面画“√”.
五.解答题(共4小题)
24.一个立体图形,从上面看到的形状是,从正面看到的形状是.搭一个这样的立体图形,最少需要几个小正方体?最多可以有几个小正方体?
25.摆一摆,画出从前面、右面和上面看到的图形.
26.一个用小正方体木块搭成的立体图形,从前面看到的图形是,从上面看到的图形也是,搭成这样的一个立体图形最少需要 块正方体木块.
我是这样想的: .
27.一个立体图形从上面看是,从右侧面看是,要搭成这样的立体图形,至少要 个小正方体,最多可以有 个小正方体.
【教师版】
一.选择题(共7小题)
1.如图是由8个小正方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置上的小正方体的个数,则这个几何体从左面看到的是( )
A. B. C. D.
【分析】这个几何体从左面看到的是:5个正方形,左边一列3个正方形,右边一列2个正方形,下齐;据此解答即可.
【解答】解:
这个几何体从左面看到的是.
故选:D.
【点评】本题是考查从不同方向观察物体和几何图形,重点培养学生的观察想象能力.
2.如图为一个用玻璃制成的立方体,粗线部分表示一根嵌在正方体内的铁丝.下列选项中( )表示从立方体左面看到的图.
A. B. C. D.
【分析】观察图形,因为该正方体是用玻璃制成的,所以从立方体左面看到的图形中,右边面上所在的竖着的粗线是可以看见的,所以从立方体左面看到的图形应该是选项B中的图形.
【解答】解:从立方体左面看到的图形.
故选:B.
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
3.从正面看到的形状为( )
A. B. C.
【分析】该几何体从正面看共两列,每一列上小正方形的个数从左到右分别为4、3,据此可以得出答案.
【解答】解:从正面看共两列,每一列上小正方形的个数从左到右分别为4、3,
所以从正面看到的形状为A选项中的形状.
故选:A.
【点评】本题考查了从正面看几何体,要先判断从正面所看到小正方形的列数,再判断每一列上小正方体的个数.
4.从下面观察,所看到的图形是( )
A. B. C.
【分析】观察图形可得,这个图形从下面看到的图形是两行:前面一行3个正方形,后面一行1个正方形靠中间,据此即可解答问题.
【解答】解:根据题干分析可得,从下面看到的图形是.
故选:A.
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
5.一个立体图形从右面看到的形状是,从正面看到的形状是,那么从上面看到的是( )
A. B. C.
【分析】如图,由4个相同正方体组成的图形,从右面看到的是一列2个正方形,从正面看到的是4个正方形,分两行,下行3个,上行1个,右齐;从上面能看到行3个正方形.
【解答】解:如图:
一个立体图形从右面看到的形状是,从正面看到的形状是,那么从上面看到的是:.
故选:B.
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
6.是由5个小正方体组成的平面图形,下面图形( )是从上面观察到的.
A. B.
C.
【分析】观察图形可知,从从上面看到的图形是一行4个正方形,据此即可选择.
【解答】解:由5个小正方体组成的平面图形,下从上面观察到的是;
故选:B.
【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图,同学们在做题时应该细心观察,属于基础题.
7.从正面看图中的物体,看到的是什么图形?( )
A. B.
C.
【分析】从正看只能看到1行3个正方形,分居两边,左边2个,右边1个;据此得解.
【解答】解:从正面看到的图形是;
故选:C.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
二.填空题(共7小题)
8.现在有1个棱长为1厘米的正方体木块,1个长宽均为1厘米,高为2厘米的长方体木块,有3个长宽均为1厘米,高为3厘米的长方体木块.下面的三幅图是把这五个木块合并成一个立体图形时,从上面、前面、右面所看到的图形,这个合并起来的立体图形的表面积为 44 平方厘米.
【分析】根据从上面、前面、右面看到的形状,这几个木块摆成成的立体图形如图所示.棱长1厘米的正方体木块每个面都是1平方厘米;长宽均为1厘米,高为2厘米的长方体木块有2个面是1平方厘米,另外4个面中每个面相当于2个1平方厘米的面,长宽均为1厘米,高为3厘米的长方体木块有2个面积是1平方厘米的面,另外4个面中每个面相当于3个面积为1平方厘米的面.正面、后面能看到的部分都相当于6个面积是1平方厘米的面;从左面、右看到的面都相当于7个面积是1平方厘米的面;从上、下看到的都相当于9个面积是1平方厘米的面.
【解答】解:根据从上面、前面、右面看到的形状,这几个木块的摆法如下:
1×1=1(平方厘米)
(6+7+9)×2
=22×2
=44(平方厘米)
答:这个合并起来的立体图形的表面积为44平方厘米.
故答案为:44.
【点评】关键明白:从上、下看到的面的面积是相等的,从左、右面看到的面的面积是相等的,从前、后看到的面的面积是相等的.
9.用一些棱长为1cm的小正方体搭建成一个几何体,从两个角度观察所得的图形如下,那么这个几何体的体积最大是 7 cm3.
【分析】根据从正面看到的图形,我们可以判断从上面看到的图形中每一摞小正方体的最高层数,进而计算出组成这个几何体的小正方体的最多个数,进而得到这个几何体的体积最大值.
【解答】解:根据从正面看到的图形可以分析出:几何体的体积最大时,从上面看到图中每摞正方体的个数为:
2+2+1+2=7,所以这个几何体最多由7个正方体组成;
由于小正方体的棱长为1厘米,则每个小正方体的体积为1立方厘米,
故这个几何体的体积最大是7立方厘米.
故答案为:7.
【点评】解答本题的关键是根据从正面看到的图形,判断每一摞小正方体的最多个数.
10.一个立体图形从上面看是,从左面看是,要搭成这样的立体图形,至少要用 5 个小正方体,最多可以有 7 个小正方体.
【分析】从左面看,物体有两层,上层有1排,下层有两排;从上面看,物体有两排,上一排有3个小正方体,下排有1个小正方体;要搭成这样的立体图形下层需要3+1=4个小正方体,上层最少只有1个小正方体,最多可以是7个小正方体,由此即可解答.
【解答】解:最少有:4+1=5(个),
最多有:4+3=7(个),
故答案为:5,7.
【点评】此题考查了从不同方向观察物体和几何体.三视图可以锻炼学生的空间想象力和抽象思维力.
11.对于和,从 上 面看形状是不一样的,从 正 和 侧 面看形状是一样的.
【分析】通过观察,从上面看到的图形不同,第一个图形的上视图是两排,外排的一个正方形在右侧,而第二个图形的外排的一个正方形在左侧,里排两个正方形是相同的;从正面和从侧看到的图形都是有一层,含两个正方形;如下图所示.
【解答】解:
对于和,从 上面看形状是不一样的,从正和侧面看形状是一样的.
故答案为:上,正,侧.
【点评】此题考查了从不同方向观察几何体,锻炼了学生的空间想象力和抽象思维能力.
12.有一个由同样大小的小正方体搭成的立体图形,从三个不同的方向看到的形状如图,这个立体图形是由 5 个小正方体搭成的.
【分析】根据从上面看到的图形可得,这个图形的下层是3个小正方体;根据从正面和左面看到的图形可得,这个图形的上层左边一列有2个小正方体,据此即可解答问题.
【解答】解:3+2=5(个)
答:这个立体图形是由5个小正方体搭成的.
故答案为:5.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
13.有一些碗叠在桌子上,下面是从不同方向看这些碗得到的形状.这些碗一共有 28 只.
【分析】左图是从上面看到的情况,由此可知,一共是3摞碗.中图的右面部分与右图的左部分是同一摞.这三摞碗的个数之和就是一共有的个数.
【解答】解:如图
7+11+10=28(个)
答:这些碗一共有28只.
故答案为:28.
【点评】解答此题的关键是明白:中图的右面部分与右图的左部分是同一摞.
14.一个用小正方体搭成的几何体,下面是从它的两个不同方向看到的形状,要符合这两个条件,最少需要摆 8 块,最多能摆 10 块.
【分析】观察图形可知,从上面看,这个图形下层是6个小正方体,上层最少是2个正方形靠左边;最多是4个小正方体靠左边,据此即可解答问题.
【解答】解:根据题干分析可得:最少有6+2=8(个),
最多是:6+4=10(个),
下层是并排2行,每行3个小正方体;上层右边一列是1层,左边两列都是2两层;
答:最少需要摆8块,最多能摆10块.
故答案为:8;10.
【点评】此题考查了从不同方向观察物体和几何体.三视图可以锻炼孩子的空间想象力和抽象思维力.
三.判断题(共4小题)
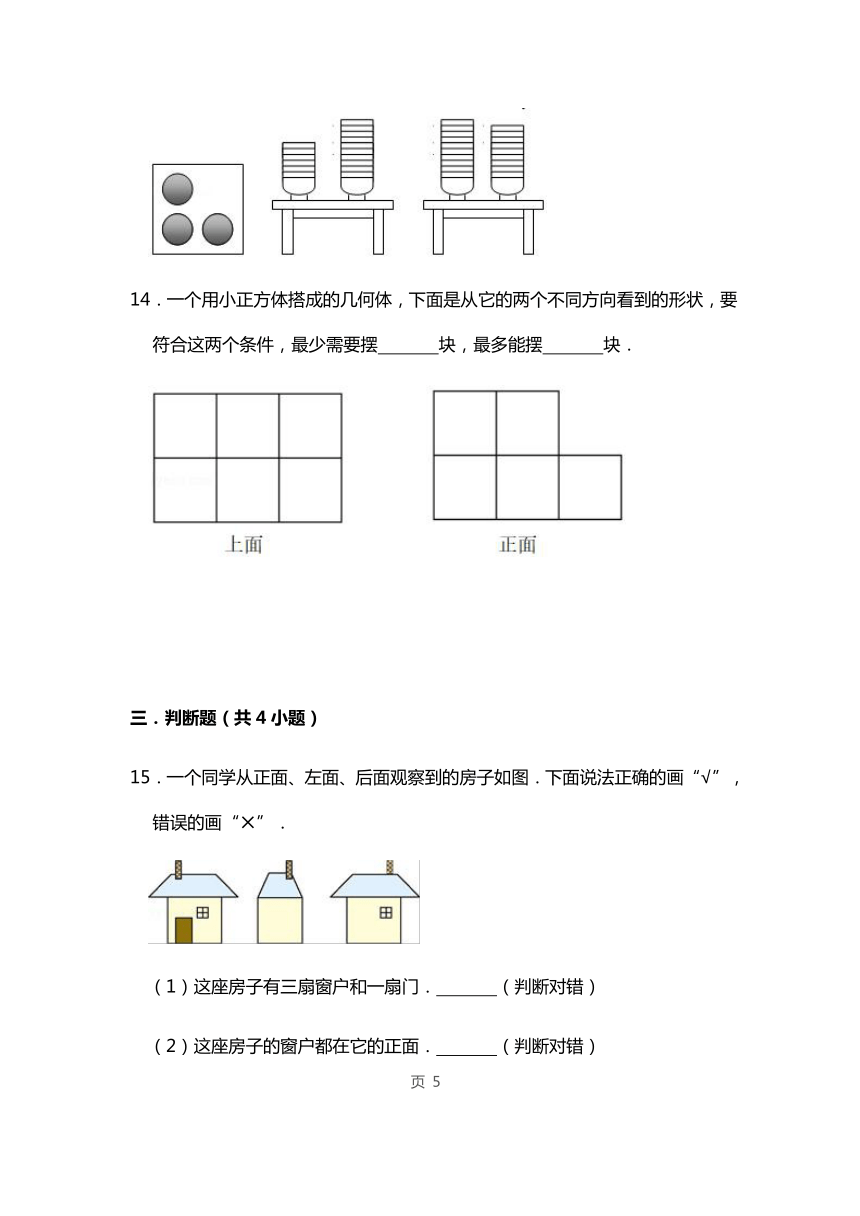
15.一个同学从正面、左面、后面观察到的房子如图.下面说法正确的画“√”,错误的画“?”.
(1)这座房子有三扇窗户和一扇门. × (判断对错)
(2)这座房子的窗户都在它的正面. × (判断对错)
(3)这座房子后边有一扇窗户. √ (判断对错)
【分析】从不同的方向观察物体,由于角度不同,所以观察到的物体的形状也不同.根据观察知:第一幅图是从正面观察到的有一个门,一个窗子;第二幅图是从侧面观察到的没有窗子,第三幅图是从后面观察到的有一个窗子.
【解答】解:(1)这座房子有2个窗户,1个门.
所以题干说法错误.
(2)这座房子的窗户都在屋子的正面和背面.
所以题干说法错误.
(3)这座房子后边有一扇窗户.
所以题干说法正确.
故答案为:?,?,√.
【点评】此题考查了从不同方向观察物体和几何体.它锻炼了学生的空间想象力和抽象思维能力.
16.不同的物体分别从不同的角度观察,看到的现状有可能是相同的. √ (判断对错)
【分析】对与一般的物体,从不同的位置观察物体,所看到的形状是不同的;但有特殊情况,如果这个不同物体分别是圆柱和球体,那么从不同的方向看到的形状有可能是相同的,即是一个圆形;据此判断即可.
【解答】解:如果这个不同物体分别是圆柱和球体,那么从不同的方向看到的形状有可能是相同的,即是一个圆形;原题说法正确.
故答案为:√.
【点评】解答此题的关键:根据题意,进行举例分析,进而得出结论.
17.一个立体图形,从上面看到的形状是,从正面看到的形状是.搭这样的一个立体图形,至少需要4个小立方块. × .(判断对错)
【分析】这个立方体图形,从正面看是3个正方形,说明从正面看是由3个小正方体组成的,分两层,下层2个,上层1个居左;从上面看是2个正方形,最少看到2个小正方体,据此解答.
【解答】解:根据题干分析可得,这个图形有2层,下层最少是3个正方形,上层至少1个正方形靠左边:1+2=3(个).
答:至少要用3个小正方体.
故答案为:×.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
18.一个物体由于观察的角度不同看到的形状一定也不相同. × .(判断对错)
【分析】对与一般的物体,从不同的位置观察物体,所看到的形状是不同的;但有特殊情况,如果这个物体是球体,那么从不同的方向看到的形状一样;据此判断即可.
【解答】解:由分析知;当这个物体是一个球体,那么从不同方向看到的形状都一样;所以从同一个方向观察不同的物体,看到的图形可能相同;
故答案为:×.
【点评】解答此题的关键:根据题意,进行举例分析,进而得出结论.
四.操作题(共5小题)
19.如图是用5个小正方体搭成的立体图形,分别画出从上面、正面和左面看到的形状.
【分析】这个立方体图形从正面能看到4个正方形,分两行,上行1个,下行3个,左齐;从左面能看到3个正方形,分两行,上行1个,下行2个,左齐;从上面能看到4个正方形,分两行,上行3个,下行1个,右齐.
【解答】解:
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
20.画出下列图形从前面、上面、左面看到的形状.
【分析】这个立体图形由6个相同的小正方体组成.从前面能看到5个正方形,分三行,上、中行各1个,下行3个,呈倒“T”形;从左面能看到4个正方形,分两列,左列3个,右列一个,呈“L”形;从上面能看到4个正方形,分两行,上行3个,下行1个,呈“T”形.
【解答】解:画出下列图形从前面、上面、左面看到的形状:
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
21.分别画出从正面、上面、侧面观察下面物体时看到的形状.
正面看到的形状是:
上面看到的形状是:
侧面看到的形状是:
【分析】这个立方体图形由两部分组成,左边由2个相同的小正方体组成,右边有同样的4个小正方体组成.从正面看,左部分是1个正方形,右部分是一行2个正方形;从上面看,左部分是一列2个正方形,右部分是两列正方形,每列2个,左列上面一个与右列下面一个成一行;从侧面看左边后面一个小正方体被右边前面的一个挡住,能看到一行4个正方形.
【解答】解:如图
正面看到的形状是:
上面看到的形状是:
侧面看到的形状是:
故答案为:,,.
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
22.如图的物体从上面、前面、右面看到的形状分别是什么?请在方格纸上画出来.
【分析】上图由5个相同的小正方体组成.从上面能看到5个正方形,分两行,上行3个,下行2个,呈倒“凹”字形;从前面能看到一行3个正方形;从右面能看到一行2个正方形.
下图也由5个相同的小正方体组成.从上面能看到3个正方形,分两行,上行2个,下行1个,左齐;从前面能看到4个正方形,分两列,左列3个,右列1个,下齐;从右面能看到4个正方形,分两列,左列1个,右列3个,下齐.
【解答】解:
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
23.根据下面从不同方向看到的图形摆一摆.
在摆法正确的下面画“√”.
【分析】根据图示,可得从正面看到的图形是四列,第二列是2层,其余的每列都是1层;从上面看到的图形四列,第一、二列是2层,其余的每列都是1层;从右面看是两列,第一列是1层,第两列是2层,据此即可画出图形.
【解答】解:根据题干分析摆法正确的如下:
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
五.解答题(共4小题)
24.一个立体图形,从上面看到的形状是,从正面看到的形状是.搭一个这样的立体图形,最少需要几个小正方体?最多可以有几个小正方体?
【分析】根据从上面看到的图形可得,这个图形的下层是4个小正方体;根据从正面看到的图形可得,这个图形的上层左边一列至少有1个小正方体,最多有2个正方体,据此即可解答问题.
【解答】解:根据题干分析可得:最少需要4+1=5(个)
最多需要4+2=6(个)
答:最少需要5个,最多可以有6个.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
25.摆一摆,画出从前面、右面和上面看到的图形.
【分析】观察图形可知,从前面看到的是上下两行,下面并列着3个正方形,上面有1个,在中间一个的上面;从右面看到的是两列,右面一列是上下两个正方形,左面一个;从左面看到的是两列,左面一列是上下两个正方形,右面一个;由此连线即可.
【解答】解:
【点评】此题考查了从不同方向观察问题和几何体,锻炼了学生的空间想象力和抽象思维能力.
26.一个用小正方体木块搭成的立体图形,从前面看到的图形是,从上面看到的图形也是,搭成这样的一个立体图形最少需要 5 块正方体木块.
我是这样想的: 下层是两行:前面一行3块正方形木块,后面一行1块正方形木块靠中间,上层中间一列至少有1块正方形木块,所以这个图形至少是3+1+1=5块正方体木块 .
【分析】根据从前面看到的图形,可以得出至少要4个小正方体,下面三个,上边一个;根据从上面看到的图形,可以得出至少要4个小正方体,前排3个,后排在中间有1个;这样得出3个是公共部分,只要上边中间多1个,后排中间多1个,最少要3+1+1个小正方体.
【解答】解:根据题干分析可得:下层是两行:前面一行3块正方形木块,后面一行1块正方形木块靠中间,上层中间一列至少有1块正方形木块,
所以这个图形正方体木块至少是3+1+1=5(块)
答:搭成这样的一个立体图形最少需要5个正方体木块.
故答案为:5;下层是两行:前面一行3块正方形木块,后面一行1块正方形木块靠中间,上层中间一列至少有1块正方形木块,所以这个图形至少是3+1+1=5块正方体木块.
【点评】此题应根据从前面和上面看到的形状,进行分析、比较,进而得出所求结论.
27.一个立体图形从上面看是,从右侧面看是,要搭成这样的立体图形,至少要 8 个小正方体,最多可以有 14 个小正方体.
【分析】由上面的图形可得,这个图形底层一共有4+1=5个小正方体,一共分成2行,后面一行4列,前面一行1列在左边第二;再由从右面看到的图形可得,前面一行是2层,后面一行是3层,要使小正方体最少,则只有一列上是3层,要使小正方体最多,则后面一行4列都是3层,据此即可解答问题.
【解答】解:根据题干分析可得:最少有2+1+1+1+3=8(个)
最多有2+3+3+3+3=14(个)
答:至少要用8个小正方体,最多可以有14个小正方体.
故答案为:8;14.
【点评】此题考查了从不同方向观察问题和几何体,锻炼了学生的空间想象力和抽象思维能力.
第三章:观察物体(提高版)
【学生版】
【知识点总结】
同样的物体,从不同的面看到的图形可能一样,也可能不一样。
无论从哪个角度观察,从一个点最多只能看到物体的三个面。
规则长方体中小正方体个数=层数×一层小正方体个数
不规则长方体中小正方体个数1)层数×每层可视小正方体个数
2)在前面小正方形上标数字
【习题巩固】
一.选择题(共7小题)
1.如图是由8个小正方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置上的小正方体的个数,则这个几何体从左面看到的是( )
A. B. C. D.
2.如图为一个用玻璃制成的立方体,粗线部分表示一根嵌在正方体内的铁丝.下列选项中( )表示从立方体左面看到的图.
A. B. C. D.
3.从正面看到的形状为( )
A. B. C.
4.从下面观察,所看到的图形是( )
A. B. C.
5.一个立体图形从右面看到的形状是,从正面看到的形状是,那么从上面看到的是( )
A. B. C.
6.是由5个小正方体组成的平面图形,下面图形( )是从上面观察到的.
A. B.
C.
7.从正面看图中的物体,看到的是什么图形?( )
A. B.
C.
二.填空题(共7小题)
8.现在有1个棱长为1厘米的正方体木块,1个长宽均为1厘米,高为2厘米的长方体木块,有3个长宽均为1厘米,高为3厘米的长方体木块.下面的三幅图是把这五个木块合并成一个立体图形时,从上面、前面、右面所看到的图形,这个合并起来的立体图形的表面积为 平方厘米.
9.用一些棱长为1cm的小正方体搭建成一个几何体,从两个角度观察所得的图形如下,那么这个几何体的体积最大是 cm3.
10.一个立体图形从上面看是,从左面看是,要搭成这样的立体图形,至少要用 个小正方体,最多可以有 个小正方体.
11.对于和,从 面看形状是不一样的,从 和 面看形状是一样的.
12.有一个由同样大小的小正方体搭成的立体图形,从三个不同的方向看到的形状如图,这个立体图形是由 个小正方体搭成的.
13.有一些碗叠在桌子上,下面是从不同方向看这些碗得到的形状.这些碗一共有 只.
14.一个用小正方体搭成的几何体,下面是从它的两个不同方向看到的形状,要符合这两个条件,最少需要摆 块,最多能摆 块.
三.判断题(共4小题)
15.一个同学从正面、左面、后面观察到的房子如图.下面说法正确的画“√”,错误的画“?”.
(1)这座房子有三扇窗户和一扇门. (判断对错)
(2)这座房子的窗户都在它的正面. (判断对错)
(3)这座房子后边有一扇窗户. (判断对错)
16.不同的物体分别从不同的角度观察,看到的现状有可能是相同的. (判断对错)
17.一个立体图形,从上面看到的形状是,从正面看到的形状是.搭这样的一个立体图形,至少需要4个小立方块. .(判断对错)
18.一个物体由于观察的角度不同看到的形状一定也不相同. .(判断对错)
四.操作题(共5小题)
19.如图是用5个小正方体搭成的立体图形,分别画出从上面、正面和左面看到的形状.
20.画出下列图形从前面、上面、左面看到的形状.
21.分别画出从正面、上面、侧面观察下面物体时看到的形状.
正面看到的形状是:
上面看到的形状是:
侧面看到的形状是:
22.如图的物体从上面、前面、右面看到的形状分别是什么?请在方格纸上画出来.
23.根据下面从不同方向看到的图形摆一摆.
在摆法正确的下面画“√”.
五.解答题(共4小题)
24.一个立体图形,从上面看到的形状是,从正面看到的形状是.搭一个这样的立体图形,最少需要几个小正方体?最多可以有几个小正方体?
25.摆一摆,画出从前面、右面和上面看到的图形.
26.一个用小正方体木块搭成的立体图形,从前面看到的图形是,从上面看到的图形也是,搭成这样的一个立体图形最少需要 块正方体木块.
我是这样想的: .
27.一个立体图形从上面看是,从右侧面看是,要搭成这样的立体图形,至少要 个小正方体,最多可以有 个小正方体.
【教师版】
一.选择题(共7小题)
1.如图是由8个小正方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置上的小正方体的个数,则这个几何体从左面看到的是( )
A. B. C. D.
【分析】这个几何体从左面看到的是:5个正方形,左边一列3个正方形,右边一列2个正方形,下齐;据此解答即可.
【解答】解:
这个几何体从左面看到的是.
故选:D.
【点评】本题是考查从不同方向观察物体和几何图形,重点培养学生的观察想象能力.
2.如图为一个用玻璃制成的立方体,粗线部分表示一根嵌在正方体内的铁丝.下列选项中( )表示从立方体左面看到的图.
A. B. C. D.
【分析】观察图形,因为该正方体是用玻璃制成的,所以从立方体左面看到的图形中,右边面上所在的竖着的粗线是可以看见的,所以从立方体左面看到的图形应该是选项B中的图形.
【解答】解:从立方体左面看到的图形.
故选:B.
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
3.从正面看到的形状为( )
A. B. C.
【分析】该几何体从正面看共两列,每一列上小正方形的个数从左到右分别为4、3,据此可以得出答案.
【解答】解:从正面看共两列,每一列上小正方形的个数从左到右分别为4、3,
所以从正面看到的形状为A选项中的形状.
故选:A.
【点评】本题考查了从正面看几何体,要先判断从正面所看到小正方形的列数,再判断每一列上小正方体的个数.
4.从下面观察,所看到的图形是( )
A. B. C.
【分析】观察图形可得,这个图形从下面看到的图形是两行:前面一行3个正方形,后面一行1个正方形靠中间,据此即可解答问题.
【解答】解:根据题干分析可得,从下面看到的图形是.
故选:A.
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
5.一个立体图形从右面看到的形状是,从正面看到的形状是,那么从上面看到的是( )
A. B. C.
【分析】如图,由4个相同正方体组成的图形,从右面看到的是一列2个正方形,从正面看到的是4个正方形,分两行,下行3个,上行1个,右齐;从上面能看到行3个正方形.
【解答】解:如图:
一个立体图形从右面看到的形状是,从正面看到的形状是,那么从上面看到的是:.
故选:B.
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
6.是由5个小正方体组成的平面图形,下面图形( )是从上面观察到的.
A. B.
C.
【分析】观察图形可知,从从上面看到的图形是一行4个正方形,据此即可选择.
【解答】解:由5个小正方体组成的平面图形,下从上面观察到的是;
故选:B.
【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图,同学们在做题时应该细心观察,属于基础题.
7.从正面看图中的物体,看到的是什么图形?( )
A. B.
C.
【分析】从正看只能看到1行3个正方形,分居两边,左边2个,右边1个;据此得解.
【解答】解:从正面看到的图形是;
故选:C.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
二.填空题(共7小题)
8.现在有1个棱长为1厘米的正方体木块,1个长宽均为1厘米,高为2厘米的长方体木块,有3个长宽均为1厘米,高为3厘米的长方体木块.下面的三幅图是把这五个木块合并成一个立体图形时,从上面、前面、右面所看到的图形,这个合并起来的立体图形的表面积为 44 平方厘米.
【分析】根据从上面、前面、右面看到的形状,这几个木块摆成成的立体图形如图所示.棱长1厘米的正方体木块每个面都是1平方厘米;长宽均为1厘米,高为2厘米的长方体木块有2个面是1平方厘米,另外4个面中每个面相当于2个1平方厘米的面,长宽均为1厘米,高为3厘米的长方体木块有2个面积是1平方厘米的面,另外4个面中每个面相当于3个面积为1平方厘米的面.正面、后面能看到的部分都相当于6个面积是1平方厘米的面;从左面、右看到的面都相当于7个面积是1平方厘米的面;从上、下看到的都相当于9个面积是1平方厘米的面.
【解答】解:根据从上面、前面、右面看到的形状,这几个木块的摆法如下:
1×1=1(平方厘米)
(6+7+9)×2
=22×2
=44(平方厘米)
答:这个合并起来的立体图形的表面积为44平方厘米.
故答案为:44.
【点评】关键明白:从上、下看到的面的面积是相等的,从左、右面看到的面的面积是相等的,从前、后看到的面的面积是相等的.
9.用一些棱长为1cm的小正方体搭建成一个几何体,从两个角度观察所得的图形如下,那么这个几何体的体积最大是 7 cm3.
【分析】根据从正面看到的图形,我们可以判断从上面看到的图形中每一摞小正方体的最高层数,进而计算出组成这个几何体的小正方体的最多个数,进而得到这个几何体的体积最大值.
【解答】解:根据从正面看到的图形可以分析出:几何体的体积最大时,从上面看到图中每摞正方体的个数为:
2+2+1+2=7,所以这个几何体最多由7个正方体组成;
由于小正方体的棱长为1厘米,则每个小正方体的体积为1立方厘米,
故这个几何体的体积最大是7立方厘米.
故答案为:7.
【点评】解答本题的关键是根据从正面看到的图形,判断每一摞小正方体的最多个数.
10.一个立体图形从上面看是,从左面看是,要搭成这样的立体图形,至少要用 5 个小正方体,最多可以有 7 个小正方体.
【分析】从左面看,物体有两层,上层有1排,下层有两排;从上面看,物体有两排,上一排有3个小正方体,下排有1个小正方体;要搭成这样的立体图形下层需要3+1=4个小正方体,上层最少只有1个小正方体,最多可以是7个小正方体,由此即可解答.
【解答】解:最少有:4+1=5(个),
最多有:4+3=7(个),
故答案为:5,7.
【点评】此题考查了从不同方向观察物体和几何体.三视图可以锻炼学生的空间想象力和抽象思维力.
11.对于和,从 上 面看形状是不一样的,从 正 和 侧 面看形状是一样的.
【分析】通过观察,从上面看到的图形不同,第一个图形的上视图是两排,外排的一个正方形在右侧,而第二个图形的外排的一个正方形在左侧,里排两个正方形是相同的;从正面和从侧看到的图形都是有一层,含两个正方形;如下图所示.
【解答】解:
对于和,从 上面看形状是不一样的,从正和侧面看形状是一样的.
故答案为:上,正,侧.
【点评】此题考查了从不同方向观察几何体,锻炼了学生的空间想象力和抽象思维能力.
12.有一个由同样大小的小正方体搭成的立体图形,从三个不同的方向看到的形状如图,这个立体图形是由 5 个小正方体搭成的.
【分析】根据从上面看到的图形可得,这个图形的下层是3个小正方体;根据从正面和左面看到的图形可得,这个图形的上层左边一列有2个小正方体,据此即可解答问题.
【解答】解:3+2=5(个)
答:这个立体图形是由5个小正方体搭成的.
故答案为:5.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
13.有一些碗叠在桌子上,下面是从不同方向看这些碗得到的形状.这些碗一共有 28 只.
【分析】左图是从上面看到的情况,由此可知,一共是3摞碗.中图的右面部分与右图的左部分是同一摞.这三摞碗的个数之和就是一共有的个数.
【解答】解:如图
7+11+10=28(个)
答:这些碗一共有28只.
故答案为:28.
【点评】解答此题的关键是明白:中图的右面部分与右图的左部分是同一摞.
14.一个用小正方体搭成的几何体,下面是从它的两个不同方向看到的形状,要符合这两个条件,最少需要摆 8 块,最多能摆 10 块.
【分析】观察图形可知,从上面看,这个图形下层是6个小正方体,上层最少是2个正方形靠左边;最多是4个小正方体靠左边,据此即可解答问题.
【解答】解:根据题干分析可得:最少有6+2=8(个),
最多是:6+4=10(个),
下层是并排2行,每行3个小正方体;上层右边一列是1层,左边两列都是2两层;
答:最少需要摆8块,最多能摆10块.
故答案为:8;10.
【点评】此题考查了从不同方向观察物体和几何体.三视图可以锻炼孩子的空间想象力和抽象思维力.
三.判断题(共4小题)
15.一个同学从正面、左面、后面观察到的房子如图.下面说法正确的画“√”,错误的画“?”.
(1)这座房子有三扇窗户和一扇门. × (判断对错)
(2)这座房子的窗户都在它的正面. × (判断对错)
(3)这座房子后边有一扇窗户. √ (判断对错)
【分析】从不同的方向观察物体,由于角度不同,所以观察到的物体的形状也不同.根据观察知:第一幅图是从正面观察到的有一个门,一个窗子;第二幅图是从侧面观察到的没有窗子,第三幅图是从后面观察到的有一个窗子.
【解答】解:(1)这座房子有2个窗户,1个门.
所以题干说法错误.
(2)这座房子的窗户都在屋子的正面和背面.
所以题干说法错误.
(3)这座房子后边有一扇窗户.
所以题干说法正确.
故答案为:?,?,√.
【点评】此题考查了从不同方向观察物体和几何体.它锻炼了学生的空间想象力和抽象思维能力.
16.不同的物体分别从不同的角度观察,看到的现状有可能是相同的. √ (判断对错)
【分析】对与一般的物体,从不同的位置观察物体,所看到的形状是不同的;但有特殊情况,如果这个不同物体分别是圆柱和球体,那么从不同的方向看到的形状有可能是相同的,即是一个圆形;据此判断即可.
【解答】解:如果这个不同物体分别是圆柱和球体,那么从不同的方向看到的形状有可能是相同的,即是一个圆形;原题说法正确.
故答案为:√.
【点评】解答此题的关键:根据题意,进行举例分析,进而得出结论.
17.一个立体图形,从上面看到的形状是,从正面看到的形状是.搭这样的一个立体图形,至少需要4个小立方块. × .(判断对错)
【分析】这个立方体图形,从正面看是3个正方形,说明从正面看是由3个小正方体组成的,分两层,下层2个,上层1个居左;从上面看是2个正方形,最少看到2个小正方体,据此解答.
【解答】解:根据题干分析可得,这个图形有2层,下层最少是3个正方形,上层至少1个正方形靠左边:1+2=3(个).
答:至少要用3个小正方体.
故答案为:×.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
18.一个物体由于观察的角度不同看到的形状一定也不相同. × .(判断对错)
【分析】对与一般的物体,从不同的位置观察物体,所看到的形状是不同的;但有特殊情况,如果这个物体是球体,那么从不同的方向看到的形状一样;据此判断即可.
【解答】解:由分析知;当这个物体是一个球体,那么从不同方向看到的形状都一样;所以从同一个方向观察不同的物体,看到的图形可能相同;
故答案为:×.
【点评】解答此题的关键:根据题意,进行举例分析,进而得出结论.
四.操作题(共5小题)
19.如图是用5个小正方体搭成的立体图形,分别画出从上面、正面和左面看到的形状.
【分析】这个立方体图形从正面能看到4个正方形,分两行,上行1个,下行3个,左齐;从左面能看到3个正方形,分两行,上行1个,下行2个,左齐;从上面能看到4个正方形,分两行,上行3个,下行1个,右齐.
【解答】解:
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
20.画出下列图形从前面、上面、左面看到的形状.
【分析】这个立体图形由6个相同的小正方体组成.从前面能看到5个正方形,分三行,上、中行各1个,下行3个,呈倒“T”形;从左面能看到4个正方形,分两列,左列3个,右列一个,呈“L”形;从上面能看到4个正方形,分两行,上行3个,下行1个,呈“T”形.
【解答】解:画出下列图形从前面、上面、左面看到的形状:
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
21.分别画出从正面、上面、侧面观察下面物体时看到的形状.
正面看到的形状是:
上面看到的形状是:
侧面看到的形状是:
【分析】这个立方体图形由两部分组成,左边由2个相同的小正方体组成,右边有同样的4个小正方体组成.从正面看,左部分是1个正方形,右部分是一行2个正方形;从上面看,左部分是一列2个正方形,右部分是两列正方形,每列2个,左列上面一个与右列下面一个成一行;从侧面看左边后面一个小正方体被右边前面的一个挡住,能看到一行4个正方形.
【解答】解:如图
正面看到的形状是:
上面看到的形状是:
侧面看到的形状是:
故答案为:,,.
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
22.如图的物体从上面、前面、右面看到的形状分别是什么?请在方格纸上画出来.
【分析】上图由5个相同的小正方体组成.从上面能看到5个正方形,分两行,上行3个,下行2个,呈倒“凹”字形;从前面能看到一行3个正方形;从右面能看到一行2个正方形.
下图也由5个相同的小正方体组成.从上面能看到3个正方形,分两行,上行2个,下行1个,左齐;从前面能看到4个正方形,分两列,左列3个,右列1个,下齐;从右面能看到4个正方形,分两列,左列1个,右列3个,下齐.
【解答】解:
【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.
23.根据下面从不同方向看到的图形摆一摆.
在摆法正确的下面画“√”.
【分析】根据图示,可得从正面看到的图形是四列,第二列是2层,其余的每列都是1层;从上面看到的图形四列,第一、二列是2层,其余的每列都是1层;从右面看是两列,第一列是1层,第两列是2层,据此即可画出图形.
【解答】解:根据题干分析摆法正确的如下:
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
五.解答题(共4小题)
24.一个立体图形,从上面看到的形状是,从正面看到的形状是.搭一个这样的立体图形,最少需要几个小正方体?最多可以有几个小正方体?
【分析】根据从上面看到的图形可得,这个图形的下层是4个小正方体;根据从正面看到的图形可得,这个图形的上层左边一列至少有1个小正方体,最多有2个正方体,据此即可解答问题.
【解答】解:根据题干分析可得:最少需要4+1=5(个)
最多需要4+2=6(个)
答:最少需要5个,最多可以有6个.
【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
25.摆一摆,画出从前面、右面和上面看到的图形.
【分析】观察图形可知,从前面看到的是上下两行,下面并列着3个正方形,上面有1个,在中间一个的上面;从右面看到的是两列,右面一列是上下两个正方形,左面一个;从左面看到的是两列,左面一列是上下两个正方形,右面一个;由此连线即可.
【解答】解:
【点评】此题考查了从不同方向观察问题和几何体,锻炼了学生的空间想象力和抽象思维能力.
26.一个用小正方体木块搭成的立体图形,从前面看到的图形是,从上面看到的图形也是,搭成这样的一个立体图形最少需要 5 块正方体木块.
我是这样想的: 下层是两行:前面一行3块正方形木块,后面一行1块正方形木块靠中间,上层中间一列至少有1块正方形木块,所以这个图形至少是3+1+1=5块正方体木块 .
【分析】根据从前面看到的图形,可以得出至少要4个小正方体,下面三个,上边一个;根据从上面看到的图形,可以得出至少要4个小正方体,前排3个,后排在中间有1个;这样得出3个是公共部分,只要上边中间多1个,后排中间多1个,最少要3+1+1个小正方体.
【解答】解:根据题干分析可得:下层是两行:前面一行3块正方形木块,后面一行1块正方形木块靠中间,上层中间一列至少有1块正方形木块,
所以这个图形正方体木块至少是3+1+1=5(块)
答:搭成这样的一个立体图形最少需要5个正方体木块.
故答案为:5;下层是两行:前面一行3块正方形木块,后面一行1块正方形木块靠中间,上层中间一列至少有1块正方形木块,所以这个图形至少是3+1+1=5块正方体木块.
【点评】此题应根据从前面和上面看到的形状,进行分析、比较,进而得出所求结论.
27.一个立体图形从上面看是,从右侧面看是,要搭成这样的立体图形,至少要 8 个小正方体,最多可以有 14 个小正方体.
【分析】由上面的图形可得,这个图形底层一共有4+1=5个小正方体,一共分成2行,后面一行4列,前面一行1列在左边第二;再由从右面看到的图形可得,前面一行是2层,后面一行是3层,要使小正方体最少,则只有一列上是3层,要使小正方体最多,则后面一行4列都是3层,据此即可解答问题.
【解答】解:根据题干分析可得:最少有2+1+1+1+3=8(个)
最多有2+3+3+3+3=14(个)
答:至少要用8个小正方体,最多可以有14个小正方体.
故答案为:8;14.
【点评】此题考查了从不同方向观察问题和几何体,锻炼了学生的空间想象力和抽象思维能力.
