2019-2020学年北师大版数学选修1-1第4章导数应用4.2.2第1课时课件:45张PPT
文档属性
| 名称 | 2019-2020学年北师大版数学选修1-1第4章导数应用4.2.2第1课时课件:45张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 11:20:20 | ||
图片预览











文档简介
(共45张PPT)
数
学
选修1-1
·
北师大版
新课标导学
第四章
导数应用
§2 导数在实际问题中的应用
2.2 最大值、最小值问题
第1课时 函数的最大值与最小值
1
自主预习学案
2
互动探究学案
3
课时作业学案
自主预习学案
1.函数最值的概念
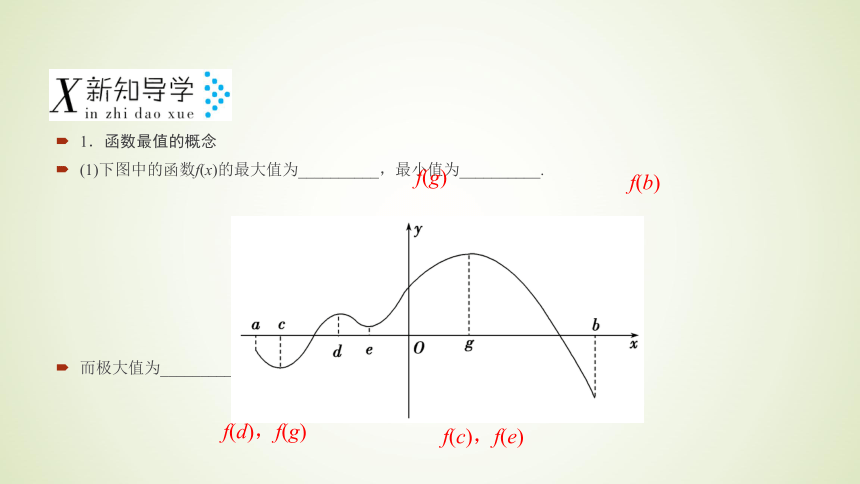
(1)下图中的函数f(x)的最大值为__________,最小值为__________.
而极大值为__________,极小值为__________.
f(g)
f(b)
f(d),f(g)
f(c),f(e)
(2)由上图还可以看出,假设函数y=f(x)在闭区间[a,b]上的图像是一条连续不断的曲线,该函数在[a,b]上一定能够取得__________与__________,若该函数在(a,b)内是__________,该函数的最值必在极值点或区间端点取得.
最大值
最小值
可导的
1.函数的最大值和最小值是一个整体性概念,最大值必须是整个区间所有函数值中的最大值,最小值必须是整个区间上所有函数值中的最小值.
2.函数的最大值、最小值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,函数的极值可以有很多,但最值只能有一个;极值只能在区间内取得,最值则可以在端点取得;有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值只要不在端点必定是极值.
A
B
3.设f(x)是[a,b]上的连续函数,且在(a,b)内可导,则下面结论中正确的是( )
A.f(x)的极值点一定是最值点
B.f(x)的最值点一定是极值点
C.f(x)在此区间上可能没有极值点
D.f(x)在此区间上可能没有最值点
[解析] 若f(x)在[a,b]上单调,则无极值点,但无论单调与否都会有最值点.
C
4.函数y=x4-2x2+5在区间[-2,2]上的最大值为__________.
[解析] y′=4x3-4x,令y′=0,即4x3-4x=0,解得x1=-1,x2=0,x3=1,又f(-2)=13,f(-1)=4,f(0)=5,f(1)=4,f(2)=13,故最大值为13.
13
5.求下列函数的最值.
(1)f(x)=-x4+2x2+3,x∈[-3,2];
(2)f(x)=x3-3x2+6x-2,x∈[-1,1].
(2)f
′(x)=3x2-6x+6=3(x2-2x+2)
=3(x-1)2+3.
∵f
′(x)在[-1,1]内恒大于0,
∴f(x)在[-1,1]上为增函数.
故x=-1时,
f(x)最小值=-12;x=1时,
f(x)最大值=2,
即f(x)的最小值为-12,最大值为2.
互动探究学案
命题方向1 利用导数求函数的最大值与最小值
典例
1
3.若连续函数在区间(a,b)内只有一个极值,那么极大值就是最大值,极小值就是最小值.
〔跟踪练习1〕
求函数f(x)=x3-2x2+1在区间[-1,2]上的最大值与最小值.
已知函数f(x)=ax3+3x+2(a∈R)的一个极值点是1.
(1)求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)求函数f(x)在[-2,3]上的最大值和最小值.
命题方向2 含参数的函数最值问题
典例
2
『规律方法』 已知函数最值求参数,可先求出函数在给定区间上的极值及函数在区间端点处的函数值,通过比较它们的大小,判断出哪个是最大值,哪个是最小值,结合已知求出参数,进而使问题得以解决.
〔跟踪练习2〕
若f(x)=ax3-6ax2+b,x∈[-1,2]的最大值是3,最小值是-29,求a、b的值.
又f(2)=8a-24a+3=-16a+3,
f(-1)=-7a+3>f(2),
∴当x=2时,
f(x)取最小值,∴-16a+3=-29,
∴a=2.
函数最值的应用主要体现在解决不等式恒成立时,求参数的取值范围问题,这是一种常见题型,主要应用分离参数法,然后转化为求函数的最值问题,在求最值时,可以借助导数求值.
函数最值的综合应用
典例
3
『规律方法』 对于根据不等式恒成立求参数的问题,可采用分离参数法,即将参数移至不等式的一端,化成m≥f(x)或m≤f(x)的形式,然后利用导数求出函数f(x)的最值,则由结论m≥f(x)max或m≤f(x)min即可求出参数m的取值范围.
用导数求最值时,注意极值与端点值的比较
典例
4
1.函数f(x)=x2-3x(|x|<2)( )
A.有最大值,但无最小值
B.有最大值,也有最小值
C.无最大值,但有最小值
D.既无最大值,也无最小值
C
A
C
4.如图是函数y=f(x)的导函数f
′(x)的图像,则下面判断正确的是( )
A.在区间(-2,1)上f(x)是增函数
B.在(1,3)上f(x)是减函数
C.在(4,5)上f(x)是增函数
D.当x=4时,f(x)取极大值
[解析] 由导函数y=f
′(x)的图像知,f(x)在(-2,1)上先减后增,在(1,3)上先增后减,在(4,5)上单调递增,x=4是f(x)的极小值点,故A、B、D错误,选C.
C
5.已知函数f(x)=2x3-6x2+a在[-2,2]上有最小值-37,求a的值,并求f(x)在[-2,2]上的最大值.
数
学
选修1-1
·
北师大版
新课标导学
第四章
导数应用
§2 导数在实际问题中的应用
2.2 最大值、最小值问题
第1课时 函数的最大值与最小值
1
自主预习学案
2
互动探究学案
3
课时作业学案
自主预习学案
1.函数最值的概念
(1)下图中的函数f(x)的最大值为__________,最小值为__________.
而极大值为__________,极小值为__________.
f(g)
f(b)
f(d),f(g)
f(c),f(e)
(2)由上图还可以看出,假设函数y=f(x)在闭区间[a,b]上的图像是一条连续不断的曲线,该函数在[a,b]上一定能够取得__________与__________,若该函数在(a,b)内是__________,该函数的最值必在极值点或区间端点取得.
最大值
最小值
可导的
1.函数的最大值和最小值是一个整体性概念,最大值必须是整个区间所有函数值中的最大值,最小值必须是整个区间上所有函数值中的最小值.
2.函数的最大值、最小值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,函数的极值可以有很多,但最值只能有一个;极值只能在区间内取得,最值则可以在端点取得;有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值只要不在端点必定是极值.
A
B
3.设f(x)是[a,b]上的连续函数,且在(a,b)内可导,则下面结论中正确的是( )
A.f(x)的极值点一定是最值点
B.f(x)的最值点一定是极值点
C.f(x)在此区间上可能没有极值点
D.f(x)在此区间上可能没有最值点
[解析] 若f(x)在[a,b]上单调,则无极值点,但无论单调与否都会有最值点.
C
4.函数y=x4-2x2+5在区间[-2,2]上的最大值为__________.
[解析] y′=4x3-4x,令y′=0,即4x3-4x=0,解得x1=-1,x2=0,x3=1,又f(-2)=13,f(-1)=4,f(0)=5,f(1)=4,f(2)=13,故最大值为13.
13
5.求下列函数的最值.
(1)f(x)=-x4+2x2+3,x∈[-3,2];
(2)f(x)=x3-3x2+6x-2,x∈[-1,1].
(2)f
′(x)=3x2-6x+6=3(x2-2x+2)
=3(x-1)2+3.
∵f
′(x)在[-1,1]内恒大于0,
∴f(x)在[-1,1]上为增函数.
故x=-1时,
f(x)最小值=-12;x=1时,
f(x)最大值=2,
即f(x)的最小值为-12,最大值为2.
互动探究学案
命题方向1 利用导数求函数的最大值与最小值
典例
1
3.若连续函数在区间(a,b)内只有一个极值,那么极大值就是最大值,极小值就是最小值.
〔跟踪练习1〕
求函数f(x)=x3-2x2+1在区间[-1,2]上的最大值与最小值.
已知函数f(x)=ax3+3x+2(a∈R)的一个极值点是1.
(1)求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)求函数f(x)在[-2,3]上的最大值和最小值.
命题方向2 含参数的函数最值问题
典例
2
『规律方法』 已知函数最值求参数,可先求出函数在给定区间上的极值及函数在区间端点处的函数值,通过比较它们的大小,判断出哪个是最大值,哪个是最小值,结合已知求出参数,进而使问题得以解决.
〔跟踪练习2〕
若f(x)=ax3-6ax2+b,x∈[-1,2]的最大值是3,最小值是-29,求a、b的值.
又f(2)=8a-24a+3=-16a+3,
f(-1)=-7a+3>f(2),
∴当x=2时,
f(x)取最小值,∴-16a+3=-29,
∴a=2.
函数最值的应用主要体现在解决不等式恒成立时,求参数的取值范围问题,这是一种常见题型,主要应用分离参数法,然后转化为求函数的最值问题,在求最值时,可以借助导数求值.
函数最值的综合应用
典例
3
『规律方法』 对于根据不等式恒成立求参数的问题,可采用分离参数法,即将参数移至不等式的一端,化成m≥f(x)或m≤f(x)的形式,然后利用导数求出函数f(x)的最值,则由结论m≥f(x)max或m≤f(x)min即可求出参数m的取值范围.
用导数求最值时,注意极值与端点值的比较
典例
4
1.函数f(x)=x2-3x(|x|<2)( )
A.有最大值,但无最小值
B.有最大值,也有最小值
C.无最大值,但有最小值
D.既无最大值,也无最小值
C
A
C
4.如图是函数y=f(x)的导函数f
′(x)的图像,则下面判断正确的是( )
A.在区间(-2,1)上f(x)是增函数
B.在(1,3)上f(x)是减函数
C.在(4,5)上f(x)是增函数
D.当x=4时,f(x)取极大值
[解析] 由导函数y=f
′(x)的图像知,f(x)在(-2,1)上先减后增,在(1,3)上先增后减,在(4,5)上单调递增,x=4是f(x)的极小值点,故A、B、D错误,选C.
C
5.已知函数f(x)=2x3-6x2+a在[-2,2]上有最小值-37,求a的值,并求f(x)在[-2,2]上的最大值.
同课章节目录
