2019-2020学年北师大版数学选修1-1第4章导数应用4章末整合提升4课件:57张PPT
文档属性
| 名称 | 2019-2020学年北师大版数学选修1-1第4章导数应用4章末整合提升4课件:57张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 00:00:00 | ||
图片预览











文档简介
(共57张PPT)
数
学
选修1-1
·
北师大版
新课标导学
第四章
导数应用
章末整合提升
1
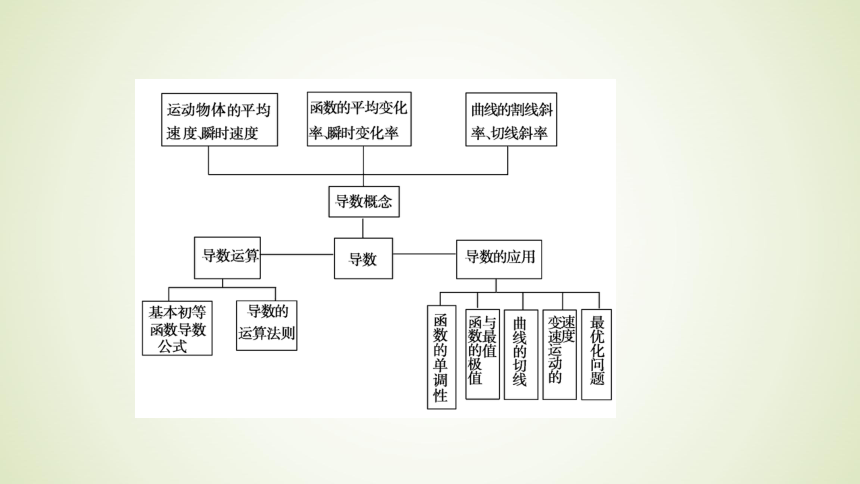
知识网络
2
知识整合
3
专题突破
知识网络
知识整合
1.函数y=f(x)在区间(a,b)上的单调性与其导数的正负的关系:
如果f
′(x)>0,那么函数在这个区间内单调递增;如果f
′(x)<0,那么函数在这个区间内单调递减;如果f
′(x)=0,那么函数在这个区间内为常数.
2.在某区间内f
′(x)>0(f
′(x)<0)是函数f(x)在此区间内为增(减)函数的充分不必要条件,如果出现个别点使得f
′(x)=0,不会影响函数f(x)在包含这些特殊点的某个区间内的单调性.所以在已知函数的单调性,求参数的取值范围时,要注意等号是否可以取到,也就是导数值为零的点需要单独验证,以免出错.
注意:当一个函数具有相同单调性的单调区间不止一个时,这些单调区间一般不能用“∪”连接,而只能用“逗号”或“和”字隔开.
3.(1)一般地,如果一个函数在某一范围内的导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图像就比较陡峭(向上或向下);反之,函数的图像就平缓一些.
(2)f
′(x0)的几何意义为曲线y=f(x)在点(x0,f(x0))处的切线的斜率.在区间(a,b)上,如果f
′(x)>0,则切线倾斜角为锐角,曲线呈向上增加状态,即函数f(x)在区间(a,b)上单调递增;如果f
′(x)<0,则切线倾斜角为钝角,曲线呈向下减少状态,即函数f(x)在区间(a,b)上单调递减.
4.(1)根据极值的定义可知,在可导函数中,若x0为极值点,则必有f
′(x0)=0(此结论常用来求参数),但f
′(x0)=0时,x0不一定为极值点,还要满足在此点附近左右两侧函数的单调性相反,单调性一致时,不能作为极值点.如函数f(x)=x3可导,且在x=0处满足f
′(0)=0,但x=0却不是极值点.
(2)求函数y=f(x)在区间[a,b]上的最值时,将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(3)如果函数y=f(x)的图像是区间[a,b]上一条连续不断的曲线,且在(a,b)上可导,则
①f(x)在[a,b]上必有最值点.
②若函数y=f(x)在区间(a,b)内只有一个导数值为0的点,且在这一点处取得极值,则该点一定是函数的最值点.
(4)有关函数零点个数的问题,可以根据函数的单调性、极值和最值,利用数形结合的思想方法,借助函数图像判断函数零点的个数.
5.(1)已知f(x)在区间D上单调,求f(x)中参数的取值范围的方法为分离参数法.通常将f
′(x)≥0(或f
′(x)≤0)的参数分离,转化为求函数的最值问题,从而求出参数的取值范围.
(2)对于证明f(x)≥(或≤)m恒成立的问题,可以转化为证明相应函数y=f(x)的最小值(或最大值)大于等于(或小于等于)m的问题.
专题突破
1.利用导数研究函数的单调性是导数的主要应用之一,其步骤为:
(1)求导数f
′(x);
(2)解不等式f
′(x)>0或f
′(x)<0;
(3)确定函数的单调增区间、减区间.
2.函数y=f(x)在区间(a,b)上的导函数为f
′(x),若f
′(x)>0总成立,则该函数在(a,b)上单调递增;若f
′(x)<0总成立,则该函数在(a,b)上单调递减.
题型一 利用导数研究函数的单调性
设函数f(x)=x3+ax2-9x-1(a<0).若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行.求:
(1)a的值;
(2)函数f(x)的单调区间.
典例
1
『规律方法』 函数的单调性与其导函数值的正负一一对应,判断函数的单调性时,可以通过计算其导函数取值的正负情况进行判断,也可以由导函数图像来判断导函数取值的正负.
1.应用导数求函数极值的一般步骤:
(1)确定函数f(x)的定义域;
(2)求方程f
′(x)=0的根;
(3)检验f
′(x)=0的根的两侧f
′(x)的符号.
若左正、右负,则f(x)在此根处取得极大值;
若左负、右正,则f(x)在此根处取得极小值.
否则,此根不是f(x)的极值点.
题型二 函数的极值与最值
2.求函数f(x)在闭区间[a,b]上的最大值、最小值的方法与步骤:
(1)求f(x)在(a,b)内的极值;
(2)将(1)中求得的极值与f(a)、f(b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.
特别地,①当f(x)在[a,b]上单调时,其最小值、最大值在区间端点取得;②当f(x)在(a,b)内只有一个极值点时,若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取得最大(或最小)值,这里(a,b)也可以是(-∞,+∞).
已知函数f(x)=x3-3ax2+2bx在x=1处有极小值-1.
(1)求函数f(x)的单调区间;
(2)求函数f(x)在闭区间[-2,2]上的最大值和最小值.
典例
2
『规律方法』 本题结合函数极值的求法,用待定系数法求出函数的解析式,再根据导数的正负确定函数的单调区间.在求最值时切记不要简单地在极值中找出最值作为结果,一定要考虑函数在区间端点处取得的函数的大小.本题主要体现了化归思想的应用.
典例
3
已知函数的单调性求参数的取值范围时,可以有两种方法,一是利用函数单调性的定义,二是利用导数法,利用导数法更为简捷.在解决问题的过程中主要处理好等号的问题,因为f
′(x)>0(或f
′(x)<0)仅是一个函数在某区间上递增(或递减)的充分不必要条件,而其充要条件是:f
′(x)≥0或(f
′(x)≤0),且使f
′(x)=0的点仅有有限个.利用导数法解决取值范围问题时可以有两个基本思路:一是将问题转化为不等式在某区间上的恒成立问题,即f
′(x)≥0或f
′(x)≤0恒成立,用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意;另一思路是先令f
′(x)>0(或f
′(x)<0),求出参数的取值范围后,再令参数取“=”,看此时f(x)是否满足题意.
题型三 求参数的取值范围问题
典例
4
1.利用导数求实际问题的最大(小)值的一般方法:
(1)分析实际问题中各个量之间的关系,正确设定所求最大或最小值的变量y与自变量x,把实际问题转化为数学问题,即列出函数关系y=f(x),根据实际问题确定y=f(x)的定义域.
(2)求方程f
′(x)=0的所有实数根.
(3)比较导函数在各个根和区间端点处的函数值的大小,根据实际问题的意义确定函数的最大值或最小值.
题型四 导数的实际应用
2.利用导数求实际问题的最大(小)值时,应注意的问题:
(1)求实际问题的最大(小)值时,一定要从问题的实际意义去考查,不符合实际意义的值应舍去.
(2)在实际问题中,由f
′(x)=0常常仅得到一个根,若能判断函数的最大(小)值在x的变化区间内部得到,则这个根处的函数值就是所求的最大(小)值.
典例
5
已知每生产1万件合格的仪器可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
[思路分析] 1.要求每天的盈利额,首先将次品率转化为正品率计算正品的产量,再乘以每件产品的利润即可表示出每天的盈利额.
2.要求日盈利额的最大值,则首先求出T′=0时的日产量,再讨论c的范围,从而确定日产量的取值.
『规律方法』 1.当题目中含有参数时,一般要对参数进行讨论,如本题中针对参数c的讨论一方面决定了日盈利额的表达式,另一方面影响了日产量的取值.
2.若参数有一定的范围,则要特别注意参数的取值范围对变量取值的影响,如本题中c为小于6的正常数,则T′=0,日产量只能取3.
题型五 导数的综合应用
典例
6
『规律方法』 用导数研究函数的性质比用初等数学的方法研究要方便的多.在知识的交汇处设计一些综合问题,突出理性思维能力,用导数作为工具研究函数的性质、函数与方程、函数与不等式方面有其新的背景和载体,同时以导数的几何意义为背景设置导数与解析几何、函数结合的综合题也甚为常见,一般以解答题形式出现,难度中等偏高.
C
2.已知函数f(x)=+ln
x,则下列选项正确的是( )
A.f(e)B.f(π)C.f(e)D.f(2.7)D
3.如图,过函数y=xsin
x+cos
x图像上点(x,y)的切线的斜率为k,若k=g(x),则函数k=g(x)的图像大致为( )
A
A
C
二、填空题
6.已知函数f(x)=(2x+1)ex,f
′(x)为f(x)的导函数,则f
′(0)的值为__________.
[解析] 由题意得f
′(x)=(2x+3)ex,则得f
′(0)=3.
3
数
学
选修1-1
·
北师大版
新课标导学
第四章
导数应用
章末整合提升
1
知识网络
2
知识整合
3
专题突破
知识网络
知识整合
1.函数y=f(x)在区间(a,b)上的单调性与其导数的正负的关系:
如果f
′(x)>0,那么函数在这个区间内单调递增;如果f
′(x)<0,那么函数在这个区间内单调递减;如果f
′(x)=0,那么函数在这个区间内为常数.
2.在某区间内f
′(x)>0(f
′(x)<0)是函数f(x)在此区间内为增(减)函数的充分不必要条件,如果出现个别点使得f
′(x)=0,不会影响函数f(x)在包含这些特殊点的某个区间内的单调性.所以在已知函数的单调性,求参数的取值范围时,要注意等号是否可以取到,也就是导数值为零的点需要单独验证,以免出错.
注意:当一个函数具有相同单调性的单调区间不止一个时,这些单调区间一般不能用“∪”连接,而只能用“逗号”或“和”字隔开.
3.(1)一般地,如果一个函数在某一范围内的导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图像就比较陡峭(向上或向下);反之,函数的图像就平缓一些.
(2)f
′(x0)的几何意义为曲线y=f(x)在点(x0,f(x0))处的切线的斜率.在区间(a,b)上,如果f
′(x)>0,则切线倾斜角为锐角,曲线呈向上增加状态,即函数f(x)在区间(a,b)上单调递增;如果f
′(x)<0,则切线倾斜角为钝角,曲线呈向下减少状态,即函数f(x)在区间(a,b)上单调递减.
4.(1)根据极值的定义可知,在可导函数中,若x0为极值点,则必有f
′(x0)=0(此结论常用来求参数),但f
′(x0)=0时,x0不一定为极值点,还要满足在此点附近左右两侧函数的单调性相反,单调性一致时,不能作为极值点.如函数f(x)=x3可导,且在x=0处满足f
′(0)=0,但x=0却不是极值点.
(2)求函数y=f(x)在区间[a,b]上的最值时,将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(3)如果函数y=f(x)的图像是区间[a,b]上一条连续不断的曲线,且在(a,b)上可导,则
①f(x)在[a,b]上必有最值点.
②若函数y=f(x)在区间(a,b)内只有一个导数值为0的点,且在这一点处取得极值,则该点一定是函数的最值点.
(4)有关函数零点个数的问题,可以根据函数的单调性、极值和最值,利用数形结合的思想方法,借助函数图像判断函数零点的个数.
5.(1)已知f(x)在区间D上单调,求f(x)中参数的取值范围的方法为分离参数法.通常将f
′(x)≥0(或f
′(x)≤0)的参数分离,转化为求函数的最值问题,从而求出参数的取值范围.
(2)对于证明f(x)≥(或≤)m恒成立的问题,可以转化为证明相应函数y=f(x)的最小值(或最大值)大于等于(或小于等于)m的问题.
专题突破
1.利用导数研究函数的单调性是导数的主要应用之一,其步骤为:
(1)求导数f
′(x);
(2)解不等式f
′(x)>0或f
′(x)<0;
(3)确定函数的单调增区间、减区间.
2.函数y=f(x)在区间(a,b)上的导函数为f
′(x),若f
′(x)>0总成立,则该函数在(a,b)上单调递增;若f
′(x)<0总成立,则该函数在(a,b)上单调递减.
题型一 利用导数研究函数的单调性
设函数f(x)=x3+ax2-9x-1(a<0).若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行.求:
(1)a的值;
(2)函数f(x)的单调区间.
典例
1
『规律方法』 函数的单调性与其导函数值的正负一一对应,判断函数的单调性时,可以通过计算其导函数取值的正负情况进行判断,也可以由导函数图像来判断导函数取值的正负.
1.应用导数求函数极值的一般步骤:
(1)确定函数f(x)的定义域;
(2)求方程f
′(x)=0的根;
(3)检验f
′(x)=0的根的两侧f
′(x)的符号.
若左正、右负,则f(x)在此根处取得极大值;
若左负、右正,则f(x)在此根处取得极小值.
否则,此根不是f(x)的极值点.
题型二 函数的极值与最值
2.求函数f(x)在闭区间[a,b]上的最大值、最小值的方法与步骤:
(1)求f(x)在(a,b)内的极值;
(2)将(1)中求得的极值与f(a)、f(b)相比较,其中最大的一个值为最大值,最小的一个值为最小值.
特别地,①当f(x)在[a,b]上单调时,其最小值、最大值在区间端点取得;②当f(x)在(a,b)内只有一个极值点时,若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取得最大(或最小)值,这里(a,b)也可以是(-∞,+∞).
已知函数f(x)=x3-3ax2+2bx在x=1处有极小值-1.
(1)求函数f(x)的单调区间;
(2)求函数f(x)在闭区间[-2,2]上的最大值和最小值.
典例
2
『规律方法』 本题结合函数极值的求法,用待定系数法求出函数的解析式,再根据导数的正负确定函数的单调区间.在求最值时切记不要简单地在极值中找出最值作为结果,一定要考虑函数在区间端点处取得的函数的大小.本题主要体现了化归思想的应用.
典例
3
已知函数的单调性求参数的取值范围时,可以有两种方法,一是利用函数单调性的定义,二是利用导数法,利用导数法更为简捷.在解决问题的过程中主要处理好等号的问题,因为f
′(x)>0(或f
′(x)<0)仅是一个函数在某区间上递增(或递减)的充分不必要条件,而其充要条件是:f
′(x)≥0或(f
′(x)≤0),且使f
′(x)=0的点仅有有限个.利用导数法解决取值范围问题时可以有两个基本思路:一是将问题转化为不等式在某区间上的恒成立问题,即f
′(x)≥0或f
′(x)≤0恒成立,用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意;另一思路是先令f
′(x)>0(或f
′(x)<0),求出参数的取值范围后,再令参数取“=”,看此时f(x)是否满足题意.
题型三 求参数的取值范围问题
典例
4
1.利用导数求实际问题的最大(小)值的一般方法:
(1)分析实际问题中各个量之间的关系,正确设定所求最大或最小值的变量y与自变量x,把实际问题转化为数学问题,即列出函数关系y=f(x),根据实际问题确定y=f(x)的定义域.
(2)求方程f
′(x)=0的所有实数根.
(3)比较导函数在各个根和区间端点处的函数值的大小,根据实际问题的意义确定函数的最大值或最小值.
题型四 导数的实际应用
2.利用导数求实际问题的最大(小)值时,应注意的问题:
(1)求实际问题的最大(小)值时,一定要从问题的实际意义去考查,不符合实际意义的值应舍去.
(2)在实际问题中,由f
′(x)=0常常仅得到一个根,若能判断函数的最大(小)值在x的变化区间内部得到,则这个根处的函数值就是所求的最大(小)值.
典例
5
已知每生产1万件合格的仪器可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
[思路分析] 1.要求每天的盈利额,首先将次品率转化为正品率计算正品的产量,再乘以每件产品的利润即可表示出每天的盈利额.
2.要求日盈利额的最大值,则首先求出T′=0时的日产量,再讨论c的范围,从而确定日产量的取值.
『规律方法』 1.当题目中含有参数时,一般要对参数进行讨论,如本题中针对参数c的讨论一方面决定了日盈利额的表达式,另一方面影响了日产量的取值.
2.若参数有一定的范围,则要特别注意参数的取值范围对变量取值的影响,如本题中c为小于6的正常数,则T′=0,日产量只能取3.
题型五 导数的综合应用
典例
6
『规律方法』 用导数研究函数的性质比用初等数学的方法研究要方便的多.在知识的交汇处设计一些综合问题,突出理性思维能力,用导数作为工具研究函数的性质、函数与方程、函数与不等式方面有其新的背景和载体,同时以导数的几何意义为背景设置导数与解析几何、函数结合的综合题也甚为常见,一般以解答题形式出现,难度中等偏高.
C
2.已知函数f(x)=+ln
x,则下列选项正确的是( )
A.f(e)
3.如图,过函数y=xsin
x+cos
x图像上点(x,y)的切线的斜率为k,若k=g(x),则函数k=g(x)的图像大致为( )
A
A
C
二、填空题
6.已知函数f(x)=(2x+1)ex,f
′(x)为f(x)的导函数,则f
′(0)的值为__________.
[解析] 由题意得f
′(x)=(2x+3)ex,则得f
′(0)=3.
3
同课章节目录
