2019-2020学年北师大版数学选修2-2第三章导数应用 第2课时课件:47张PPT
文档属性
| 名称 | 2019-2020学年北师大版数学选修2-2第三章导数应用 第2课时课件:47张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 00:00:00 | ||
图片预览











文档简介
(共47张PPT)
第三章
导数应用
本章知识概述:导数应用包括两个方面:一是利用导数作为一种工具在解决函数问题中应用;二是导数在分析和解决实际问题中的应用,在教科书中分为两节.
第一部分主要是利用导数来研究函数的单调性与极大、极小值,是导数在研究和处理函数性质问题的一个重要应用.
第二部分主要是应用导数方法解决现实中的变化趋势和最优化问题,解决这类问题的关键是函数模型的建立,从导数角度看,主要是导数在数学上的研究成果的应用.导数在现实生活中有着广泛的应用,在物理学中的力学、电学、运动、做功、受热膨胀等问题的解决都离不开导数.在日常生活中,利用导数处理最优化问题简单方便.导数是人们在解决现实生活问题中的伟大发明.
本章的学习重点是应用导数解决函数的单调性、极值、最值问题,同时利用导数的概念形成过程中的思想分析问题并建立导数模型.学习的难点是导数方法的应
§1 函数的单调性与极值
第2课时 函数的极值
1
自主预习学案
2
互动探究学案
3
课时作业学案
自主预习学案
苏轼《题西林壁》中的诗句“横看成岭侧成峰,远近高
低各不同”,描述的是庐山的高低起伏,错落有致.在群山
之中,各个山峰的顶端,虽然不一定是群山的最高处,但它
却是其附近的最高点.
那么,在数学上,这种现象如何来刻画呢?
1.如图所示,在包含x0的一个区间(a,b)内,函数y=f(x)在任何一点的函数值都不大于x0点的函数值,称点x0为函数y=f(x)的__________,其函数值f(x0)为函数的_________.
极大值点
极大值
图1
图2
如图2所示,在包含x0的一个区间(a,b)内,函数y=f(x)在任何一点的函数值都不小于x0点的函数值,称点x0为函数y=f(x)的_________,其函数值f(x0)为函数的_______.
_______________统称为极值,极大值点与极小值点统称为极值点.
极小值点
极小值
极大值与极小值
2.如果函数y=f(x)在区间(a,x0)上是_____的,在区间(x0,b)上是_____的,则x0是极大值点,f(x0)是极大值.
如果函数y=f(x)在区间(a,x0)上是_____的,在区间(x0,b)上是_____的,则x0是极小值点,f(x0)是极小值.
利用导数与函数单调性的关系,我们可以把极大值的问题通过下表表示出来.
增加
x
(a,x0)
x0
(x0,b)
f′(x)
+
0
-
y=f(x)
增加?
极大值
减少?
减少
减少
增加
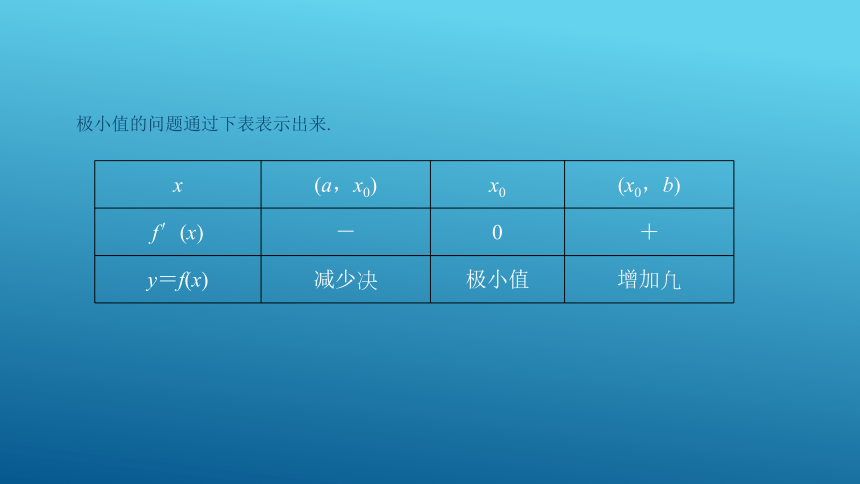
极小值的问题通过下表表示出来.
x
(a,x0)
x0
(x0,b)
f′(x)
-
0
+
y=f(x)
减少?
极小值
增加?
3.求函数极值点的步骤
一般情况下,我们可以通过如下步骤求出函数y=f(x)的极值点:
(1)求出导数f′(x).
(2)解方程______________.
(3)对于方程______________的每一个解x0,分析f′(x)在x0___________的符号(即f(x)的单调性),确定极值点:
①若f′(x)在x0两侧的符号___________,则x0为极大值点;
②若f′(x)在x0两侧的符号___________,则x0为极小值点;
③若f′(x)在x0两侧的符号_____,则x0不是极值点.
f′(x)=0
f′(x)=0
左、右两侧
“左正右负”
“左负右正”
相同
1.下列四个函数:①y=x3;②y=x2+1;③y=|x|;④y=2x.在x=0处取得极小值的函数是( )
A.①②
B.②③
C.③④
D.①③
[解析] ①y=x3在R上单调递增,无极值;
②y=x2+1在(-∞,0)上单调递减,在(0,+∞)上单调递增,故②正确;
③y=|x|在(-∞,0)上单调递减在(0,+∞)上单调递增,故③正确;
④y=2x在R上单调递增,故④不正确.
∴选B.
B
2.已知a为函数f(x)=x3-12x的极小值点,则a=( )
A.-4
B.-2
C.4
D.2
[解析] 由题意得f
′(x)=3x2-12,
由f
′(x)=0得x=±2,当x∈(-∞,-2)时,f
′(x)>0,函数f(x)单调递增,
当x∈(-2,2)时,f
′(x)<0,函数f(x)单调递减,
当x∈(2,+∞)时,f
′(x)>0,函数f(x)单调递增,所以a=2.
D
3.已知函数f(x)=ax3+bx2+cx,其导函数y=f′(x)的图像经过点(1,0),(2,0),如下图所示,下列说法不正确的是__.
②f(x)有两个极值点;
③当x=2时函数取得极小值;
④当x=1时函数取得极大值.
[解析] 由题图可以看出,当x∈(-∞,1)时,f′(x)>0;当x∈(1,2)时,f′(x)<0;当x∈(2,+∞)时,f′(x)>0,所以f(x)有两个极值点,为1和2,且当x=2时函数取得极小值,当x=1时函数取得极大值.故只有①说法不正确.
①
互动探究学案
求函数y=3x3-x+1的极值.
[思路分析] 首先对函数求导,然后求方程y′=0的根,再检查y′在方程根左、右两侧的值的符号.如果左正右负,那么y在这个根处取得极大值;如果左负右正,那么y在这个根处取得极小值.
命题方向1 利用导数求函数的极值
典例
1
『规律总结』 利用导数求函数极值的步骤:
(1)确定函数的定义域.
(2)求导数f
′(x).
(3)解方程f
′(x)=0得方程的根.
(4)利用方程f
′(x)=0的根将定义域分成若干个小开区间,列表,判定导函数在各个小开区间的符号.
(5)确定函数的极值,如果f
′(x)的符号在x0处由正(负)变负(正),则f(x)在x0处取得极大(小)值.
〔跟踪练习1〕
(1)(2019·武汉高二检测)函数f(x)的定义域为开区间(a,b),其导函数f
′(x)在(a,b)内的图像如图所示,则函数f(x)在开区间(a,b)内极小值点的个数为
( )
A.1
B.2
C.3
D.4
A
B
已知f(x)=ax5-bx3+c在x=±1处的极大值为4,极小值为0,试确定a、b、c的值.
[思路分析] 本题的关键是理解“f(x)在x=±1处的极大值为4,极小值为0”的含义.即x=±1是方程f
′(x)=0的两个根且在根x=±1处f
′(x)取值左、右异号.
[解析] f
′(x)=5ax4-3bx2=x2(5ax2-3b).
由题意,f
′(x)=0应有根x=±1,故5a=3b,
于是f
′(x)=5ax2(x2-1)
命题方向2 求参数的值或取值范围问题
典例
2
『规律总结』 已知函数极值,确定函数解析式中的参数时,注意以下两点:
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解.
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.
〔跟踪练习2〕
(1)已知函数f(x)的导数f
′(x)=a(x+1)(x-a),若f(x)在x=a处取到极大值,则a的取值范围是( )
A.(-∞,-1)
B.(0,+∞)
C.(0,1)
D.(-1,0)
(2)设a∈R,若函数y=ex+ax,x∈R,有大于零的极值点,则( )
D
C
[解析] (1)若a<-1,∵f
′(x)=a(x+1)(x-a),
∴f(x)在(-∞,a)上单调递减,在(a,-1)上单调递增,∴f(x)在x=a处取得极小值,与题意不符;
若-1若a>0,则f(x)在(-1,a)上单调递减,在(a,+∞)上单调递增,与题意矛盾,∴选D.
(2)y′=ex+a,由题意知a<0.
∵函数有大于零的极值点,x=x0为其极值点,
∴ex0+a=0,x0>0,∴a<-1,故选C.
如图是函数y=f(x)的导函数y=f
′(x)的图像,对此图像,有如下结论:
①在区间(-2,1)内f(x)是增函数;
②在区间(1,3)内f(x)是减函数;
③x=2时,f(x)取到极大值;
④在x=3时,f(x)取到极小值.
其中正确的是__(将你认为正确的序号填在横线上).
[思路分析] 给出了y=f
′(x)的图像,应观察图像找出使f
′(x)>0与
f
′(x)<0的x的取值范围,并区分f
′(x)的符号由正到负和由负到正,再做判断.
命题方向3 函数与其导函数图像间的关系问题
③
典例
3
『规律总结』 有关给出图像研究函数性质的题目,要分清给的是f(x)的图像还是f
′(x)的图像,若给的是f(x)的图像,应先找出f(x)的单调区间及极(最)值点,如果给的是f
′(x)的图像,应先找出f
′(x)的正负区间及由正变负还是由负变正,然后结合题目特点分析求解.
〔跟踪练习3〕
设函数f(x)在R上可导,其导函数为f
′(x),且函数y=(1-x)f
′(x)的图像如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
D
[解析] 由函数的图像可知,f
′(-2)=0,f
′(1)=0,f
′(2)=0,并且当x<-2时,f
′(x)>0,当-2<x<1,f
′(x)<0,函数f(x)有极大值f(-2).
又当1<x<2时,f
′(x)<0,当x>2时,f
′(x)>0,故函数f(x)有极小值f(2).
故选D.
在函数的综合问题中,涉及方程的根的个数时,常以函数极值为工具,并用数形结合来判断方程根的个数或已知方程根的个数来确定字母参数的取值范围.
已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极大值,直线y=m与y=f(x)的图像有三个不同的交点,求m的取值范围.
有关函数极值的综合应用
典例
4
(2)∵f(x)在x=-1处取得极大值,
∴f
′(-1)=3×(-1)2-3a=0,∴a=1.
∴f(x)=x3-3x-1,f
′(x)=3x2-3,
由f
′(x)=0解得x1=-1,x2=1.
由(1)中f(x)的单调性可知,f(x)在x=-1处取得极大值f(-1)=1,
在x=1处取得极小值f(1)=-3.
∵直线y=m与函数y=f(x)的图像有三个不同的交点,又f(-3)=-19<-3,f(3)=17>1,
结合f(x)的单调性可知,m的取值范围是(-3,1).
『规律总结』 函数极值可应用于求曲线与曲线(或坐标轴)的交点,求方程根的个数等问题时,往往先构造函数,利用极值,并结合图像来解决.
〔跟踪练习4〕
设a为实数,函数f(x)=x3-x2-x+a.
(1)求f(x)的极值;
(2)当a在什么范围内取值时,曲线f(x)与x轴有且只有一个交点?
极小值是f(1)=a-1.
(2)函数f(x)=x3-x2-x+a
=(x-1)2(x+1)+a-1,
由此可知,x取足够大的正数时,有f(x)>0,x取足够小的负数时,有f(x)<0,
所以曲线y=f(x)与x轴至少有一个交点.
已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a、b的值.
[辨析] 根据极值定义,函数先减后增为极小值,函数先增后减为极大值,上述解法未验证x=-1时函数两侧的单调性,导致错误.
注意极大值点与极小值点的区别
典例
5
[正解] (在上述解法之后继续)当a=1,b=3时,f
′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去;
当a=2,b=9时,f
′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈[-3,-1]时,f(x)为减函数;当x∈[-1,+∞)时,f(x)为增函数,
所以f(x)在x=-1时取得极小值.因此a=2,b=9.
[警示] f(x)在x=x0处有极值时,一定有f
′(x0)=0,f(x0)可能为极大值,也可能为极小值,应检验f(x)在x=x0两侧的符号后才可下结论;若f
′(x0)=0,则f(x)未必在x=x0处取得极值,只有确认x1〔跟踪练习5〕
若函数f(x)=x3-2mx2+m2x在x=1处取得极小值,则实数m=__.
[解析] ∵f
′(x)=(3x-m)(x-m),
由题意得:f
′(1)=(3-m)(1-m)=0,
∴m=3或m=1.
经检验知,当m=3时,在x=1处取得极大值.
当m=1时,在x=1处取得极小值.∴m=1.
1
1.函数f(x)的定义域为R,导函数f
′(x)的图像如图所示,则函数f(x)( )
A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点
C
[解析] f
′(x)的符号由正变负,则f(x0)是极大值,f
′(x)的符号由负变正,则f(x0)是极小值.由图像易知有两个极大值点,两个极小值点.
A
3.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围是_______________.
[解析] f
′(x)=3x2+2ax+a+6,
∵f(x)有极大值与极小值,
∴f
′(x)=0有两不等实根,
∴Δ=4a2-12(a+6)>0,∴a<-3或a>6.
a<-3或a>6
4.(2018·全国卷Ⅰ文,21(1))已知函数f(x)=aex-ln
x-1.设x=2是f(x)的极值点,求a,并求f(x)的单调区间.
第三章
导数应用
本章知识概述:导数应用包括两个方面:一是利用导数作为一种工具在解决函数问题中应用;二是导数在分析和解决实际问题中的应用,在教科书中分为两节.
第一部分主要是利用导数来研究函数的单调性与极大、极小值,是导数在研究和处理函数性质问题的一个重要应用.
第二部分主要是应用导数方法解决现实中的变化趋势和最优化问题,解决这类问题的关键是函数模型的建立,从导数角度看,主要是导数在数学上的研究成果的应用.导数在现实生活中有着广泛的应用,在物理学中的力学、电学、运动、做功、受热膨胀等问题的解决都离不开导数.在日常生活中,利用导数处理最优化问题简单方便.导数是人们在解决现实生活问题中的伟大发明.
本章的学习重点是应用导数解决函数的单调性、极值、最值问题,同时利用导数的概念形成过程中的思想分析问题并建立导数模型.学习的难点是导数方法的应
§1 函数的单调性与极值
第2课时 函数的极值
1
自主预习学案
2
互动探究学案
3
课时作业学案
自主预习学案
苏轼《题西林壁》中的诗句“横看成岭侧成峰,远近高
低各不同”,描述的是庐山的高低起伏,错落有致.在群山
之中,各个山峰的顶端,虽然不一定是群山的最高处,但它
却是其附近的最高点.
那么,在数学上,这种现象如何来刻画呢?
1.如图所示,在包含x0的一个区间(a,b)内,函数y=f(x)在任何一点的函数值都不大于x0点的函数值,称点x0为函数y=f(x)的__________,其函数值f(x0)为函数的_________.
极大值点
极大值
图1
图2
如图2所示,在包含x0的一个区间(a,b)内,函数y=f(x)在任何一点的函数值都不小于x0点的函数值,称点x0为函数y=f(x)的_________,其函数值f(x0)为函数的_______.
_______________统称为极值,极大值点与极小值点统称为极值点.
极小值点
极小值
极大值与极小值
2.如果函数y=f(x)在区间(a,x0)上是_____的,在区间(x0,b)上是_____的,则x0是极大值点,f(x0)是极大值.
如果函数y=f(x)在区间(a,x0)上是_____的,在区间(x0,b)上是_____的,则x0是极小值点,f(x0)是极小值.
利用导数与函数单调性的关系,我们可以把极大值的问题通过下表表示出来.
增加
x
(a,x0)
x0
(x0,b)
f′(x)
+
0
-
y=f(x)
增加?
极大值
减少?
减少
减少
增加
极小值的问题通过下表表示出来.
x
(a,x0)
x0
(x0,b)
f′(x)
-
0
+
y=f(x)
减少?
极小值
增加?
3.求函数极值点的步骤
一般情况下,我们可以通过如下步骤求出函数y=f(x)的极值点:
(1)求出导数f′(x).
(2)解方程______________.
(3)对于方程______________的每一个解x0,分析f′(x)在x0___________的符号(即f(x)的单调性),确定极值点:
①若f′(x)在x0两侧的符号___________,则x0为极大值点;
②若f′(x)在x0两侧的符号___________,则x0为极小值点;
③若f′(x)在x0两侧的符号_____,则x0不是极值点.
f′(x)=0
f′(x)=0
左、右两侧
“左正右负”
“左负右正”
相同
1.下列四个函数:①y=x3;②y=x2+1;③y=|x|;④y=2x.在x=0处取得极小值的函数是( )
A.①②
B.②③
C.③④
D.①③
[解析] ①y=x3在R上单调递增,无极值;
②y=x2+1在(-∞,0)上单调递减,在(0,+∞)上单调递增,故②正确;
③y=|x|在(-∞,0)上单调递减在(0,+∞)上单调递增,故③正确;
④y=2x在R上单调递增,故④不正确.
∴选B.
B
2.已知a为函数f(x)=x3-12x的极小值点,则a=( )
A.-4
B.-2
C.4
D.2
[解析] 由题意得f
′(x)=3x2-12,
由f
′(x)=0得x=±2,当x∈(-∞,-2)时,f
′(x)>0,函数f(x)单调递增,
当x∈(-2,2)时,f
′(x)<0,函数f(x)单调递减,
当x∈(2,+∞)时,f
′(x)>0,函数f(x)单调递增,所以a=2.
D
3.已知函数f(x)=ax3+bx2+cx,其导函数y=f′(x)的图像经过点(1,0),(2,0),如下图所示,下列说法不正确的是__.
②f(x)有两个极值点;
③当x=2时函数取得极小值;
④当x=1时函数取得极大值.
[解析] 由题图可以看出,当x∈(-∞,1)时,f′(x)>0;当x∈(1,2)时,f′(x)<0;当x∈(2,+∞)时,f′(x)>0,所以f(x)有两个极值点,为1和2,且当x=2时函数取得极小值,当x=1时函数取得极大值.故只有①说法不正确.
①
互动探究学案
求函数y=3x3-x+1的极值.
[思路分析] 首先对函数求导,然后求方程y′=0的根,再检查y′在方程根左、右两侧的值的符号.如果左正右负,那么y在这个根处取得极大值;如果左负右正,那么y在这个根处取得极小值.
命题方向1 利用导数求函数的极值
典例
1
『规律总结』 利用导数求函数极值的步骤:
(1)确定函数的定义域.
(2)求导数f
′(x).
(3)解方程f
′(x)=0得方程的根.
(4)利用方程f
′(x)=0的根将定义域分成若干个小开区间,列表,判定导函数在各个小开区间的符号.
(5)确定函数的极值,如果f
′(x)的符号在x0处由正(负)变负(正),则f(x)在x0处取得极大(小)值.
〔跟踪练习1〕
(1)(2019·武汉高二检测)函数f(x)的定义域为开区间(a,b),其导函数f
′(x)在(a,b)内的图像如图所示,则函数f(x)在开区间(a,b)内极小值点的个数为
( )
A.1
B.2
C.3
D.4
A
B
已知f(x)=ax5-bx3+c在x=±1处的极大值为4,极小值为0,试确定a、b、c的值.
[思路分析] 本题的关键是理解“f(x)在x=±1处的极大值为4,极小值为0”的含义.即x=±1是方程f
′(x)=0的两个根且在根x=±1处f
′(x)取值左、右异号.
[解析] f
′(x)=5ax4-3bx2=x2(5ax2-3b).
由题意,f
′(x)=0应有根x=±1,故5a=3b,
于是f
′(x)=5ax2(x2-1)
命题方向2 求参数的值或取值范围问题
典例
2
『规律总结』 已知函数极值,确定函数解析式中的参数时,注意以下两点:
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解.
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.
〔跟踪练习2〕
(1)已知函数f(x)的导数f
′(x)=a(x+1)(x-a),若f(x)在x=a处取到极大值,则a的取值范围是( )
A.(-∞,-1)
B.(0,+∞)
C.(0,1)
D.(-1,0)
(2)设a∈R,若函数y=ex+ax,x∈R,有大于零的极值点,则( )
D
C
[解析] (1)若a<-1,∵f
′(x)=a(x+1)(x-a),
∴f(x)在(-∞,a)上单调递减,在(a,-1)上单调递增,∴f(x)在x=a处取得极小值,与题意不符;
若-1
(2)y′=ex+a,由题意知a<0.
∵函数有大于零的极值点,x=x0为其极值点,
∴ex0+a=0,x0>0,∴a<-1,故选C.
如图是函数y=f(x)的导函数y=f
′(x)的图像,对此图像,有如下结论:
①在区间(-2,1)内f(x)是增函数;
②在区间(1,3)内f(x)是减函数;
③x=2时,f(x)取到极大值;
④在x=3时,f(x)取到极小值.
其中正确的是__(将你认为正确的序号填在横线上).
[思路分析] 给出了y=f
′(x)的图像,应观察图像找出使f
′(x)>0与
f
′(x)<0的x的取值范围,并区分f
′(x)的符号由正到负和由负到正,再做判断.
命题方向3 函数与其导函数图像间的关系问题
③
典例
3
『规律总结』 有关给出图像研究函数性质的题目,要分清给的是f(x)的图像还是f
′(x)的图像,若给的是f(x)的图像,应先找出f(x)的单调区间及极(最)值点,如果给的是f
′(x)的图像,应先找出f
′(x)的正负区间及由正变负还是由负变正,然后结合题目特点分析求解.
〔跟踪练习3〕
设函数f(x)在R上可导,其导函数为f
′(x),且函数y=(1-x)f
′(x)的图像如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
D
[解析] 由函数的图像可知,f
′(-2)=0,f
′(1)=0,f
′(2)=0,并且当x<-2时,f
′(x)>0,当-2<x<1,f
′(x)<0,函数f(x)有极大值f(-2).
又当1<x<2时,f
′(x)<0,当x>2时,f
′(x)>0,故函数f(x)有极小值f(2).
故选D.
在函数的综合问题中,涉及方程的根的个数时,常以函数极值为工具,并用数形结合来判断方程根的个数或已知方程根的个数来确定字母参数的取值范围.
已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极大值,直线y=m与y=f(x)的图像有三个不同的交点,求m的取值范围.
有关函数极值的综合应用
典例
4
(2)∵f(x)在x=-1处取得极大值,
∴f
′(-1)=3×(-1)2-3a=0,∴a=1.
∴f(x)=x3-3x-1,f
′(x)=3x2-3,
由f
′(x)=0解得x1=-1,x2=1.
由(1)中f(x)的单调性可知,f(x)在x=-1处取得极大值f(-1)=1,
在x=1处取得极小值f(1)=-3.
∵直线y=m与函数y=f(x)的图像有三个不同的交点,又f(-3)=-19<-3,f(3)=17>1,
结合f(x)的单调性可知,m的取值范围是(-3,1).
『规律总结』 函数极值可应用于求曲线与曲线(或坐标轴)的交点,求方程根的个数等问题时,往往先构造函数,利用极值,并结合图像来解决.
〔跟踪练习4〕
设a为实数,函数f(x)=x3-x2-x+a.
(1)求f(x)的极值;
(2)当a在什么范围内取值时,曲线f(x)与x轴有且只有一个交点?
极小值是f(1)=a-1.
(2)函数f(x)=x3-x2-x+a
=(x-1)2(x+1)+a-1,
由此可知,x取足够大的正数时,有f(x)>0,x取足够小的负数时,有f(x)<0,
所以曲线y=f(x)与x轴至少有一个交点.
已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a、b的值.
[辨析] 根据极值定义,函数先减后增为极小值,函数先增后减为极大值,上述解法未验证x=-1时函数两侧的单调性,导致错误.
注意极大值点与极小值点的区别
典例
5
[正解] (在上述解法之后继续)当a=1,b=3时,f
′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去;
当a=2,b=9时,f
′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈[-3,-1]时,f(x)为减函数;当x∈[-1,+∞)时,f(x)为增函数,
所以f(x)在x=-1时取得极小值.因此a=2,b=9.
[警示] f(x)在x=x0处有极值时,一定有f
′(x0)=0,f(x0)可能为极大值,也可能为极小值,应检验f(x)在x=x0两侧的符号后才可下结论;若f
′(x0)=0,则f(x)未必在x=x0处取得极值,只有确认x1
若函数f(x)=x3-2mx2+m2x在x=1处取得极小值,则实数m=__.
[解析] ∵f
′(x)=(3x-m)(x-m),
由题意得:f
′(1)=(3-m)(1-m)=0,
∴m=3或m=1.
经检验知,当m=3时,在x=1处取得极大值.
当m=1时,在x=1处取得极小值.∴m=1.
1
1.函数f(x)的定义域为R,导函数f
′(x)的图像如图所示,则函数f(x)( )
A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点
C
[解析] f
′(x)的符号由正变负,则f(x0)是极大值,f
′(x)的符号由负变正,则f(x0)是极小值.由图像易知有两个极大值点,两个极小值点.
A
3.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围是_______________.
[解析] f
′(x)=3x2+2ax+a+6,
∵f(x)有极大值与极小值,
∴f
′(x)=0有两不等实根,
∴Δ=4a2-12(a+6)>0,∴a<-3或a>6.
a<-3或a>6
4.(2018·全国卷Ⅰ文,21(1))已知函数f(x)=aex-ln
x-1.设x=2是f(x)的极值点,求a,并求f(x)的单调区间.
同课章节目录
