2.1.1平面(共29张PPT)
图片预览







文档简介
(共29张PPT)
2.1.1 平面
新课导入
桌子给我们平面的印象
黑板给我们平面的印象
墙面给我们平面的印象
平静的水面给我们平面的印象
平面的概念
光滑的桌面、平静的湖面、镜面和黑板面等都给我们以平面的印象。
几何中的“平面”是现实平面加以抽象的结果。
立体几何中的平面的特点:
1.平的
不是凹凸不平
2.四周无限延展
没有边界
3.不计大小
无所谓面积
4.不计厚薄
没有体积
平面的表示方法
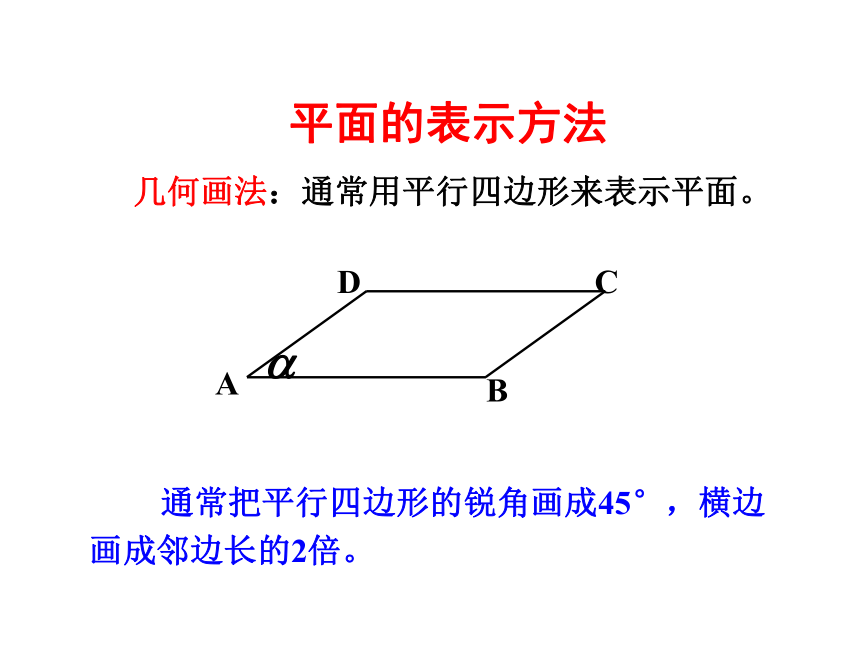
几何画法:通常用平行四边形来表示平面。
通常把平行四边形的锐角画成45°,横边画成邻边长的2倍。
A
D
C
B
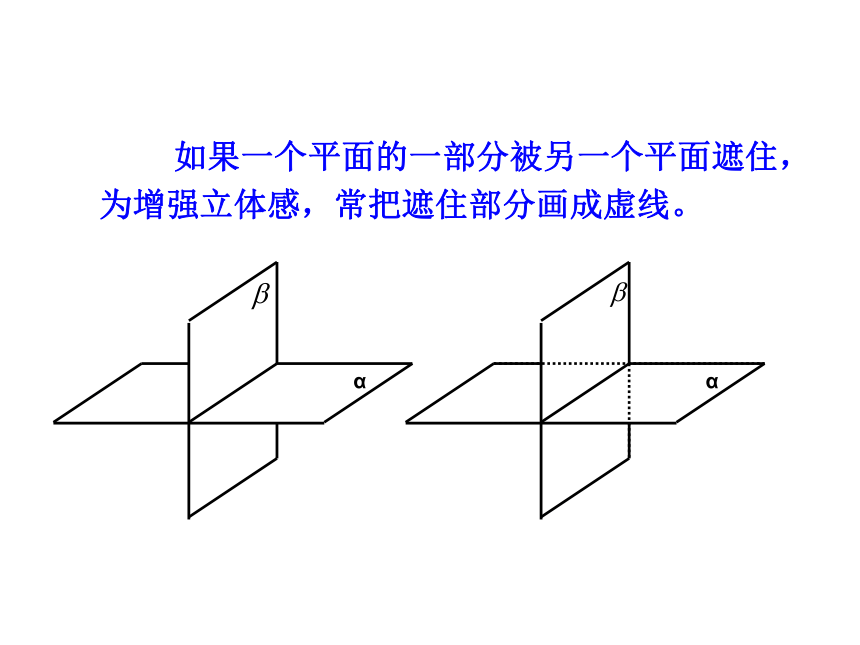
如果一个平面的一部分被另一个平面遮住,为增强立体感,常把遮住部分画成虚线。
α
α
符号表示:通常用希腊字母α,β,γ等来表示,如:平面α,平面β;也可用表示平行四边形的四个顶点,或两个相对顶点的大写字母来表示,如:平面ABCD,平面AC,平面BD。
A
D
C
B
点A在平面α内:记为:A∈α
A
B
α
点与平面的位置关系
点B不在平面α上:记为:B α
若一条直线l与平面α有一个公共点,直线l是否在平面α内?若直线l与平面α有两个公共点呢?
思考
把直尺和桌面分别看做一条直线和一个平面。(1)若直尺上的一个点在桌面内,直线可能不在面上。(2)若直尺上有两个点放在桌面上,整个直尺就落在了桌面上。
公理1 如果一条直线上两点在一个平面内,那么这条直线在此平面内。
α
l
A
B
符号表示:
1.可以用来判定一条直线是否在平面内.即要判定直线在平面内,只需确定直线上两个点在平面内即可。
2.可以用来判定点在平面内,即如果直线在平面内、点在直线上,则点在平面内。
3.表明平面是“平的”。
公理1的作用
直线l在平面α内:记为:l∈α
直线与平面的位置关系
直线l不在平面α上:记为:l α
α
生活中,我们常看到用三脚架固定相机等物品。这样做有什么原因吗?
思考
公理2 过不在同一直线上的三点,有且只有一个平面。
α
A
C
B
可记做平面ABC
公理2是确定平面的依据。
把三角板的一角放在桌面上,三角板所在平面与桌面只有一个交点吗?
在长方体中,两个相交平面都有一条公共直线.是否能够推广?
思考
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
1.是判定两个平面相交,即如果两个平面有一个公共点,那么这两个平面相交;
2.是判定点在直线上,即点若是某两个平面的公共点,那么这点就在这两个平面的交线上。
公理3的作用
长方体的ABCD-A‘B’C‘D’中如图三个面所在平面分别记做α,β,γ,用适当的符号填空。
∈
∈
∈
∈
∈
∈
∩
∩
∩
∩
∩
α
β
γ
例一
证明:经过两条平行直线,有且只有一个平面。
证明:设直线a、b满足a平行于b ,由平行线的定义,直线a、b在同一平面内,这就是说,过直线a、b有平面α。
设点A为直线a上任一点,则点A在直线b外,点A和直线b在过直线a、b的平面α内,由公理3的推论1,过点A和直线b的平面只有一个.过直线a、b的平面只有一个。
a
b
α
A
例二
课堂小结
A∈a
B∈a
A∈α
B∈α
α
a
α
A
b
a
B
a
A
α
A
B
b∩α=A
a∥α
点与直线位置关系
点与平面位置关系
直线与平面位置关系
公理1 如果一条直线上两点在一个平面内,那么这条直线在此平面内。
公理2 过不在同一直线上的三点,有且只有一个平面。
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
三个公理
随堂练习
1.已知命题:
①10个平面重叠起来,要比5个平面重叠起来要厚。
②有一个平面的长是50m,宽是20m。
③黑板面是平面。
④平面是绝对的平,没有大小,没有厚度,可以无限
延展的抽象的数学概念。
其中正确的命题是( )
④
2.填空题.
(1)一条直线可以将平面分成两部分,那么一个平面可以把空间分成 个部分。
(2)两个平面可以将空间分成 个部分。
(3)用符号表示:“点A在直线L 上, L在平面α 外”,是 。
2
3或4
A∈L,L α
3.下列叙述正确的是( )
因为P ∈ α,Q ∈α, 所以PQ ∈ α。
因为P ∈ α,Q ∈β所以α∩ β= PQ 。
C. 因为AB α, C ∈ AB ,D ∈AB 所以 CD ∈α
D. 因为AB α, AB β,所以A ∈ (α∩β)且 B ∈ (α∩β)
∩
∩
∩
D
4.两个平面能将空间分成几部分?
3或 4
两个平面相交
??
?
1
3
4
2
1
3
2
两个平面平行
5.三个平面能将空间分成几部分?
1
3
2
4
4
6
7
4个或6个或7个
2.1.1 平面
新课导入
桌子给我们平面的印象
黑板给我们平面的印象
墙面给我们平面的印象
平静的水面给我们平面的印象
平面的概念
光滑的桌面、平静的湖面、镜面和黑板面等都给我们以平面的印象。
几何中的“平面”是现实平面加以抽象的结果。
立体几何中的平面的特点:
1.平的
不是凹凸不平
2.四周无限延展
没有边界
3.不计大小
无所谓面积
4.不计厚薄
没有体积
平面的表示方法
几何画法:通常用平行四边形来表示平面。
通常把平行四边形的锐角画成45°,横边画成邻边长的2倍。
A
D
C
B
如果一个平面的一部分被另一个平面遮住,为增强立体感,常把遮住部分画成虚线。
α
α
符号表示:通常用希腊字母α,β,γ等来表示,如:平面α,平面β;也可用表示平行四边形的四个顶点,或两个相对顶点的大写字母来表示,如:平面ABCD,平面AC,平面BD。
A
D
C
B
点A在平面α内:记为:A∈α
A
B
α
点与平面的位置关系
点B不在平面α上:记为:B α
若一条直线l与平面α有一个公共点,直线l是否在平面α内?若直线l与平面α有两个公共点呢?
思考
把直尺和桌面分别看做一条直线和一个平面。(1)若直尺上的一个点在桌面内,直线可能不在面上。(2)若直尺上有两个点放在桌面上,整个直尺就落在了桌面上。
公理1 如果一条直线上两点在一个平面内,那么这条直线在此平面内。
α
l
A
B
符号表示:
1.可以用来判定一条直线是否在平面内.即要判定直线在平面内,只需确定直线上两个点在平面内即可。
2.可以用来判定点在平面内,即如果直线在平面内、点在直线上,则点在平面内。
3.表明平面是“平的”。
公理1的作用
直线l在平面α内:记为:l∈α
直线与平面的位置关系
直线l不在平面α上:记为:l α
α
生活中,我们常看到用三脚架固定相机等物品。这样做有什么原因吗?
思考
公理2 过不在同一直线上的三点,有且只有一个平面。
α
A
C
B
可记做平面ABC
公理2是确定平面的依据。
把三角板的一角放在桌面上,三角板所在平面与桌面只有一个交点吗?
在长方体中,两个相交平面都有一条公共直线.是否能够推广?
思考
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
1.是判定两个平面相交,即如果两个平面有一个公共点,那么这两个平面相交;
2.是判定点在直线上,即点若是某两个平面的公共点,那么这点就在这两个平面的交线上。
公理3的作用
长方体的ABCD-A‘B’C‘D’中如图三个面所在平面分别记做α,β,γ,用适当的符号填空。
∈
∈
∈
∈
∈
∈
∩
∩
∩
∩
∩
α
β
γ
例一
证明:经过两条平行直线,有且只有一个平面。
证明:设直线a、b满足a平行于b ,由平行线的定义,直线a、b在同一平面内,这就是说,过直线a、b有平面α。
设点A为直线a上任一点,则点A在直线b外,点A和直线b在过直线a、b的平面α内,由公理3的推论1,过点A和直线b的平面只有一个.过直线a、b的平面只有一个。
a
b
α
A
例二
课堂小结
A∈a
B∈a
A∈α
B∈α
α
a
α
A
b
a
B
a
A
α
A
B
b∩α=A
a∥α
点与直线位置关系
点与平面位置关系
直线与平面位置关系
公理1 如果一条直线上两点在一个平面内,那么这条直线在此平面内。
公理2 过不在同一直线上的三点,有且只有一个平面。
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
三个公理
随堂练习
1.已知命题:
①10个平面重叠起来,要比5个平面重叠起来要厚。
②有一个平面的长是50m,宽是20m。
③黑板面是平面。
④平面是绝对的平,没有大小,没有厚度,可以无限
延展的抽象的数学概念。
其中正确的命题是( )
④
2.填空题.
(1)一条直线可以将平面分成两部分,那么一个平面可以把空间分成 个部分。
(2)两个平面可以将空间分成 个部分。
(3)用符号表示:“点A在直线L 上, L在平面α 外”,是 。
2
3或4
A∈L,L α
3.下列叙述正确的是( )
因为P ∈ α,Q ∈α, 所以PQ ∈ α。
因为P ∈ α,Q ∈β所以α∩ β= PQ 。
C. 因为AB α, C ∈ AB ,D ∈AB 所以 CD ∈α
D. 因为AB α, AB β,所以A ∈ (α∩β)且 B ∈ (α∩β)
∩
∩
∩
D
4.两个平面能将空间分成几部分?
3或 4
两个平面相交
??
?
1
3
4
2
1
3
2
两个平面平行
5.三个平面能将空间分成几部分?
1
3
2
4
4
6
7
4个或6个或7个
