必修2第2章 空间点,线,面的位置关系章末复习(共30张PPT)
文档属性
| 名称 | 必修2第2章 空间点,线,面的位置关系章末复习(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 392.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 13:15:35 | ||
图片预览





文档简介
(共30张PPT)
第二章 点、直线、平面之间的位置关系
2.1空间点、直线、平面之间的位置关系
2.2直线、平面平行的判定及其性质
2.3直线、平面垂直的判定及其性质
学法指导
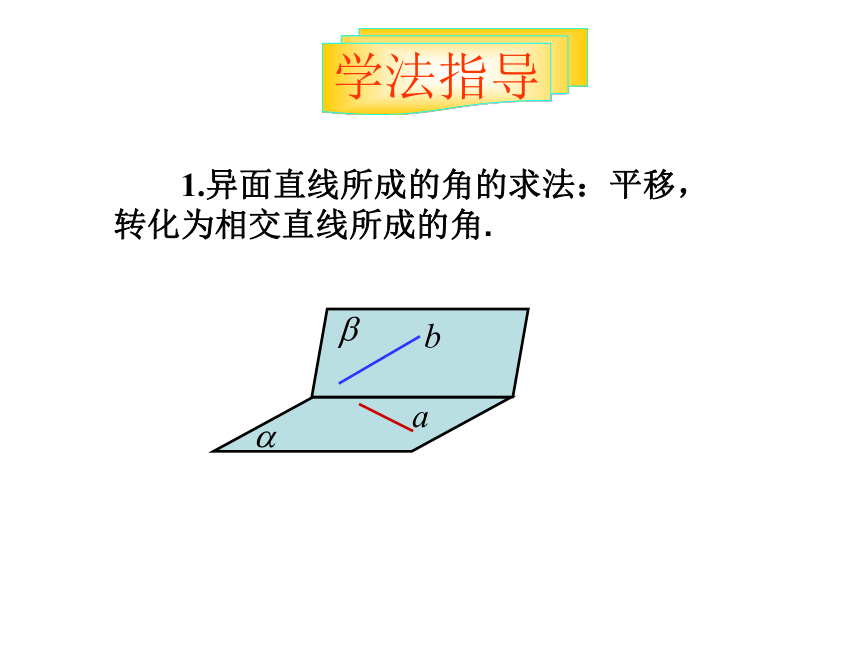
1.异面直线所成的角的求法:平移,转化为相交直线所成的角.
2.线线平行、线面平行、线线垂直、线面垂直的关系经常互相转化.要在证明题中灵活应用.
要点总结
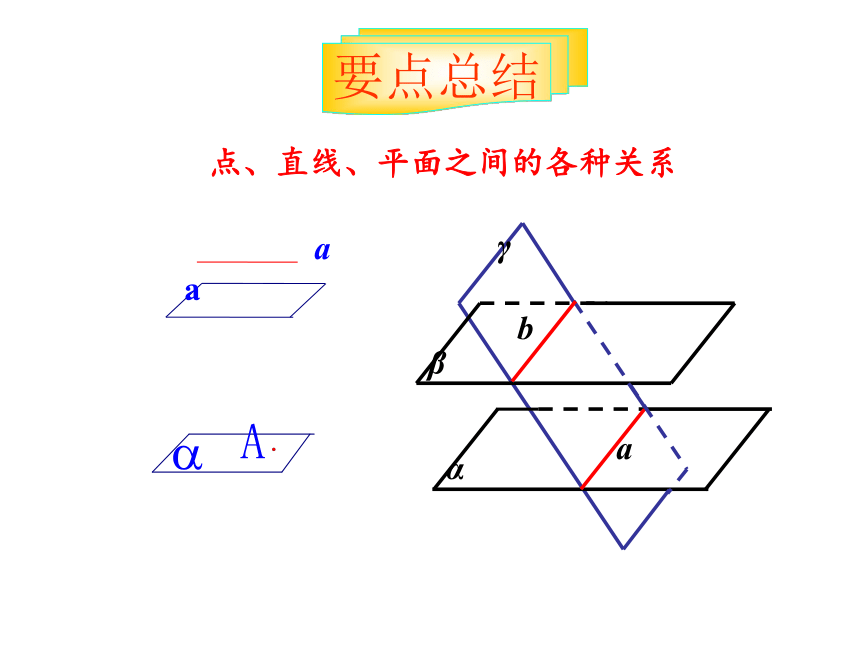
点、直线、平面之间的各种关系
2.1空间点、直线、平面之间的位置关系
2.1.1平面
点与直线位置关系
点与平面位置关系
直线与平面位置关系
点在直线上
点在直线外
点在平面上
点在平面外
直线在平面上
直线在平面外
公理1 如果一条直线上两点在一个平面内,那么这条直线在此平面内.
公理2 过不在同一直线上的三点,有且只有一个平面.
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
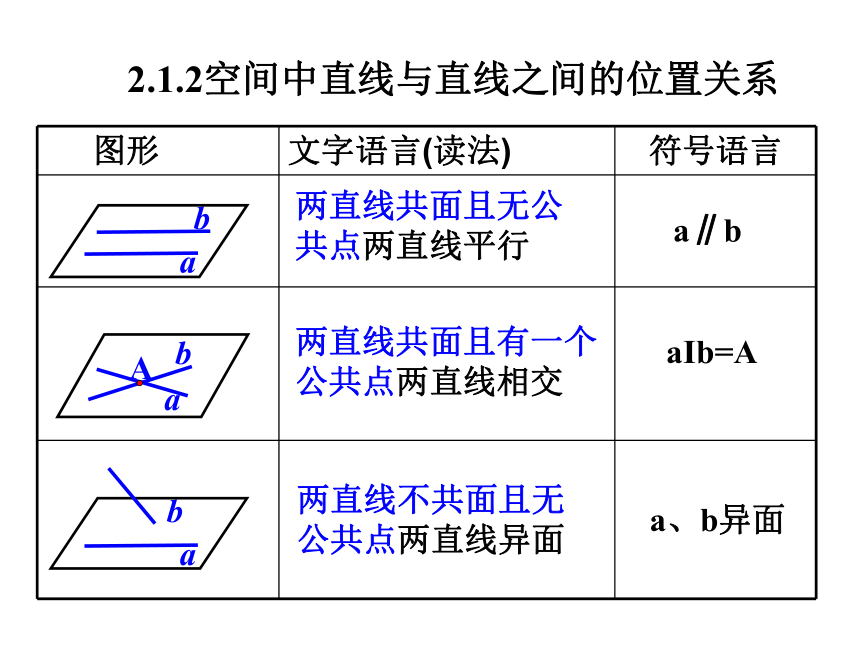
2.1.2空间中直线与直线之间的位置关系
a∥b
两直线不共面且无公共点两直线异面
两直线共面且有一个公共点两直线相交
两直线共面且无公共点两直线平行
a、b异面
aIb=A
图形 文字语言(读法) 符号语言
公理4:
在空间平行于同一条直线的两条直线互相平行.
空间中,如果两个角的两边分别对应平行, 那么这两个角相等或互补.
等角定理:
异面直线所成的角:
平移,转化为相交直线所成的角.
不同在任何一个平面内的两条直线叫做异面直线.
异面直线的定义:
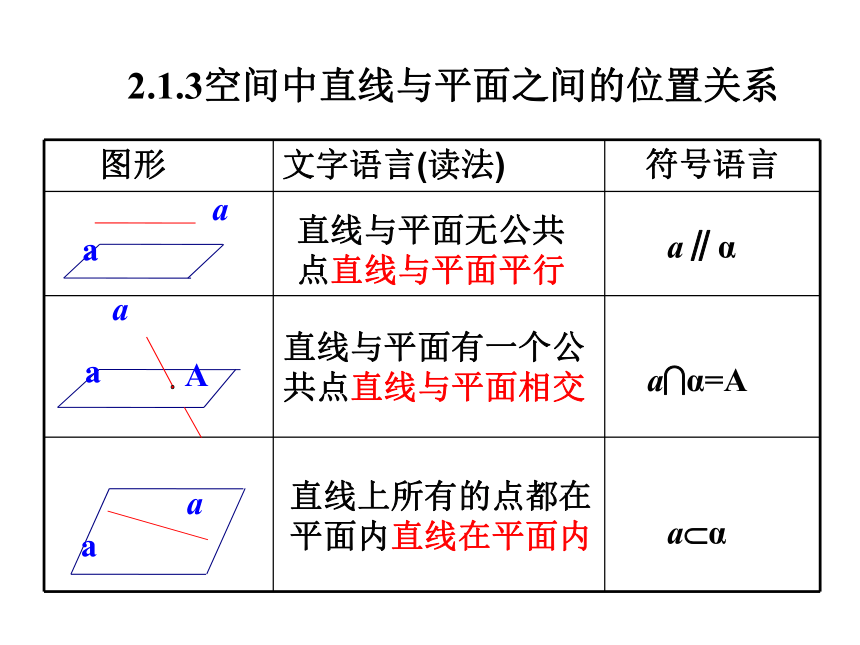
2.1.3空间中直线与平面之间的位置关系
直线上所有的点都在平面内直线在平面内
直线与平面有一个公共点直线与平面相交
直线与平面无公共点直线与平面平行
aIα=A
a∥α
a?α
图形 文字语言(读法) 符号语言
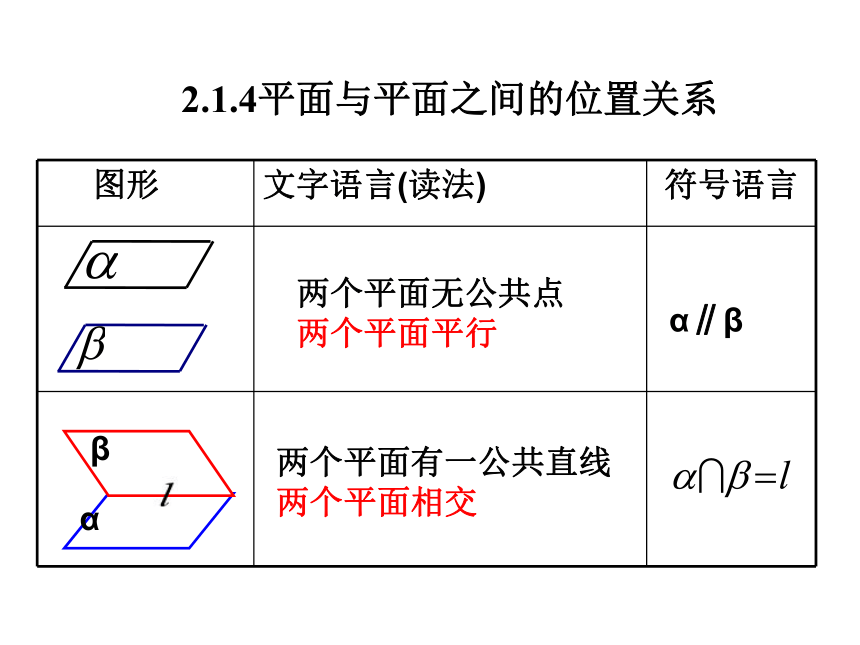
2.1.4平面与平面之间的位置关系
两个平面有一公共直线两个平面相交
两个平面无公共点两个平面平行
α∥β
图形 文字语言(读法) 符号语言
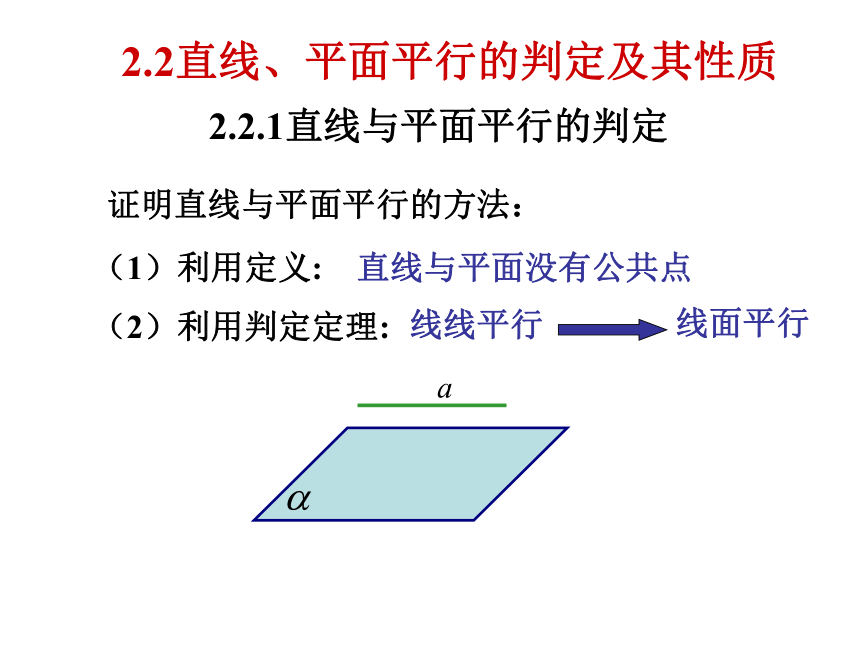
2.2直线、平面平行的判定及其性质
2.2.1直线与平面平行的判定
证明直线与平面平行的方法:
(1)利用定义:
(2)利用判定定理:
直线与平面没有公共点
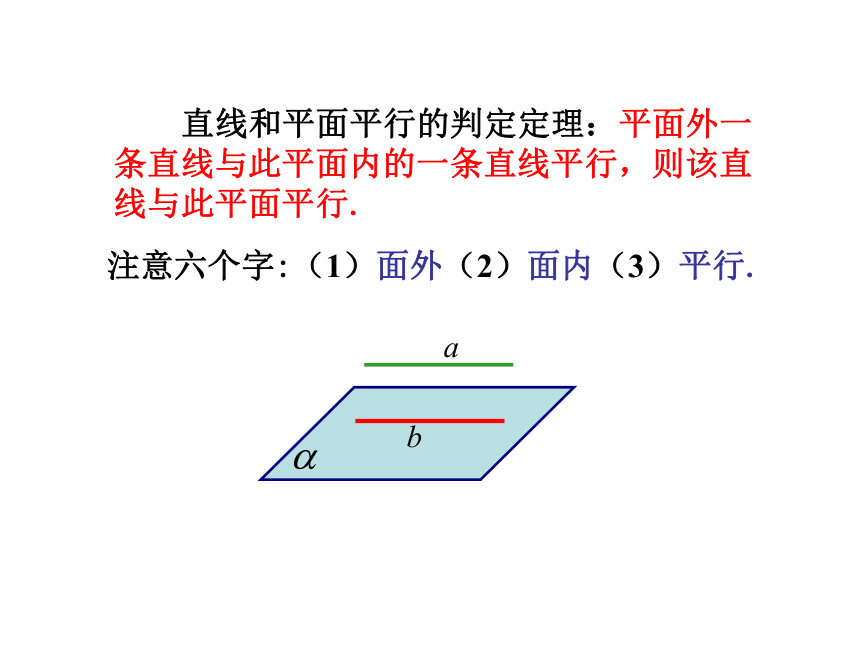
注意六个字:(1)面外(2)面内(3)平行.
直线和平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
2.2.2平面与平面平行的判定
证明平面与平面平行的方法:
(1)利用定义:
(2)利用判定定理:
平面与平面没有公共点
平面和平面平行的判定定理:一个平面内有两条相交直线与此另一平面平行,则这两个平面平行.
注意两点:
(1)有两条直线平行于同一个平面. (2)这两条直线必须相交.
2.2.3直线与平面平行的性质
线面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.
注意:使用定理时,必须具备三个条件:
(1)直线a与平面α平行,
(2)平面α与平面β相交于直线b,
(3)直线a在平面β内.
2.2.4平面与平面平行的性质
平面和平面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
2.3直线、平面垂直的判定及其性质
2.3.1直线与平面垂直的判定
直线和平面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
证明直线与平面垂直的方法:
(1)利用定义:
(2)利用判定定理:
直线与平面内每条直线都垂直
关键:线不在多,相交则行
斜线和射影所成的锐角叫做这条直线和平面所成的角.范围是:[0°,90°].
2.3.2平面与平面垂直的判定
从一条直线引出的两个半平面所组成的图形叫做二面角.
二面角的概念:
二面角的平面角:用来度量二面角的大小.
平面和平面垂直的判定定理:如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直.
2.3.3直线与平面垂直的性质
直线和平面垂直的性质定理:垂直于同一平面的两直线互相平行.
2.3.4 平面与平面垂直的性质
平面和平面垂直的性质定理:如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
证明线面垂直的两种方法:
线线垂直→线面垂直
面面垂直→线面垂直
高考热点
1.异面直线所成的角的求法.
2. 线面平行的性质的应用.
3. 线面垂直的判定.
本章易错点
1.直线和平面平行的判定定理注意六个字:(1)面外(2)面内(3)平行.
2.平面和平面平行的判定定理注意两点:
(1)有两条直线平行于同一个平面. (2)这两条直线必须相交.
3.直线与平面平行的性质注意必须具备三个条件:
(1)直线a与平面α平行,
(2)平面α与平面β相交于直线b,
(3)直线a在平面β内.
4.直线和平面垂直的判定定理线不在多,相交则行.
第二章 点、直线、平面之间的位置关系
2.1空间点、直线、平面之间的位置关系
2.2直线、平面平行的判定及其性质
2.3直线、平面垂直的判定及其性质
学法指导
1.异面直线所成的角的求法:平移,转化为相交直线所成的角.
2.线线平行、线面平行、线线垂直、线面垂直的关系经常互相转化.要在证明题中灵活应用.
要点总结
点、直线、平面之间的各种关系
2.1空间点、直线、平面之间的位置关系
2.1.1平面
点与直线位置关系
点与平面位置关系
直线与平面位置关系
点在直线上
点在直线外
点在平面上
点在平面外
直线在平面上
直线在平面外
公理1 如果一条直线上两点在一个平面内,那么这条直线在此平面内.
公理2 过不在同一直线上的三点,有且只有一个平面.
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
2.1.2空间中直线与直线之间的位置关系
a∥b
两直线不共面且无公共点两直线异面
两直线共面且有一个公共点两直线相交
两直线共面且无公共点两直线平行
a、b异面
aIb=A
图形 文字语言(读法) 符号语言
公理4:
在空间平行于同一条直线的两条直线互相平行.
空间中,如果两个角的两边分别对应平行, 那么这两个角相等或互补.
等角定理:
异面直线所成的角:
平移,转化为相交直线所成的角.
不同在任何一个平面内的两条直线叫做异面直线.
异面直线的定义:
2.1.3空间中直线与平面之间的位置关系
直线上所有的点都在平面内直线在平面内
直线与平面有一个公共点直线与平面相交
直线与平面无公共点直线与平面平行
aIα=A
a∥α
a?α
图形 文字语言(读法) 符号语言
2.1.4平面与平面之间的位置关系
两个平面有一公共直线两个平面相交
两个平面无公共点两个平面平行
α∥β
图形 文字语言(读法) 符号语言
2.2直线、平面平行的判定及其性质
2.2.1直线与平面平行的判定
证明直线与平面平行的方法:
(1)利用定义:
(2)利用判定定理:
直线与平面没有公共点
注意六个字:(1)面外(2)面内(3)平行.
直线和平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
2.2.2平面与平面平行的判定
证明平面与平面平行的方法:
(1)利用定义:
(2)利用判定定理:
平面与平面没有公共点
平面和平面平行的判定定理:一个平面内有两条相交直线与此另一平面平行,则这两个平面平行.
注意两点:
(1)有两条直线平行于同一个平面. (2)这两条直线必须相交.
2.2.3直线与平面平行的性质
线面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.
注意:使用定理时,必须具备三个条件:
(1)直线a与平面α平行,
(2)平面α与平面β相交于直线b,
(3)直线a在平面β内.
2.2.4平面与平面平行的性质
平面和平面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
2.3直线、平面垂直的判定及其性质
2.3.1直线与平面垂直的判定
直线和平面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
证明直线与平面垂直的方法:
(1)利用定义:
(2)利用判定定理:
直线与平面内每条直线都垂直
关键:线不在多,相交则行
斜线和射影所成的锐角叫做这条直线和平面所成的角.范围是:[0°,90°].
2.3.2平面与平面垂直的判定
从一条直线引出的两个半平面所组成的图形叫做二面角.
二面角的概念:
二面角的平面角:用来度量二面角的大小.
平面和平面垂直的判定定理:如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直.
2.3.3直线与平面垂直的性质
直线和平面垂直的性质定理:垂直于同一平面的两直线互相平行.
2.3.4 平面与平面垂直的性质
平面和平面垂直的性质定理:如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
证明线面垂直的两种方法:
线线垂直→线面垂直
面面垂直→线面垂直
高考热点
1.异面直线所成的角的求法.
2. 线面平行的性质的应用.
3. 线面垂直的判定.
本章易错点
1.直线和平面平行的判定定理注意六个字:(1)面外(2)面内(3)平行.
2.平面和平面平行的判定定理注意两点:
(1)有两条直线平行于同一个平面. (2)这两条直线必须相交.
3.直线与平面平行的性质注意必须具备三个条件:
(1)直线a与平面α平行,
(2)平面α与平面β相交于直线b,
(3)直线a在平面β内.
4.直线和平面垂直的判定定理线不在多,相交则行.
