必修2第一章空间几何体 单元复习(共25张PPT)
文档属性
| 名称 | 必修2第一章空间几何体 单元复习(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 885.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 13:16:54 | ||
图片预览




文档简介
(共25张PPT)
第一章 空间几何体
1.1 空间几何体的结构
1.2 空间几何体的三视图和直观图
1.3 空间几何体的表面积和体积
学法指导
1. 有两个面互相平行,其余各面都是平行四边形的几何体不一定是棱柱.要用棱柱定义判断.
2. 圆柱可以由矩形旋转得到,圆锥可以有直角三角形旋转得到,圆台直角梯形旋转得到.
3. 棱台、圆台可看作是棱锥、圆锥由平面截去一部分所得,所以棱台、圆台的问题常转化为棱锥、圆锥.
4. 画空间几何体的三视图时注意长对正,高平齐,宽相等.
5. 画空间几何体的直观图时注意x,y轴相交成45°,平行x轴的线段的长度保持不变.平行y轴的线段的长度变为原来的一半.
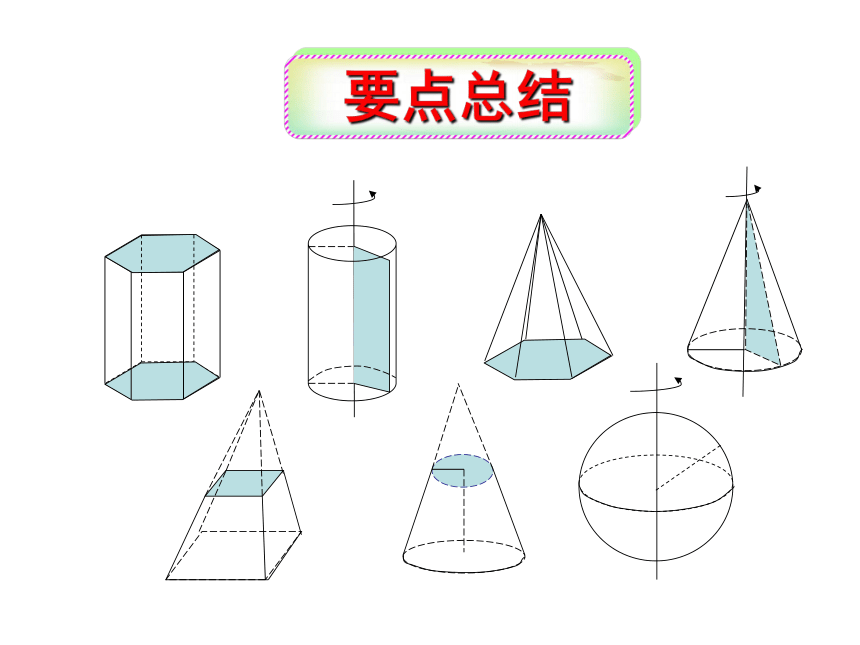
要点总结
1.1空间几何体的结构
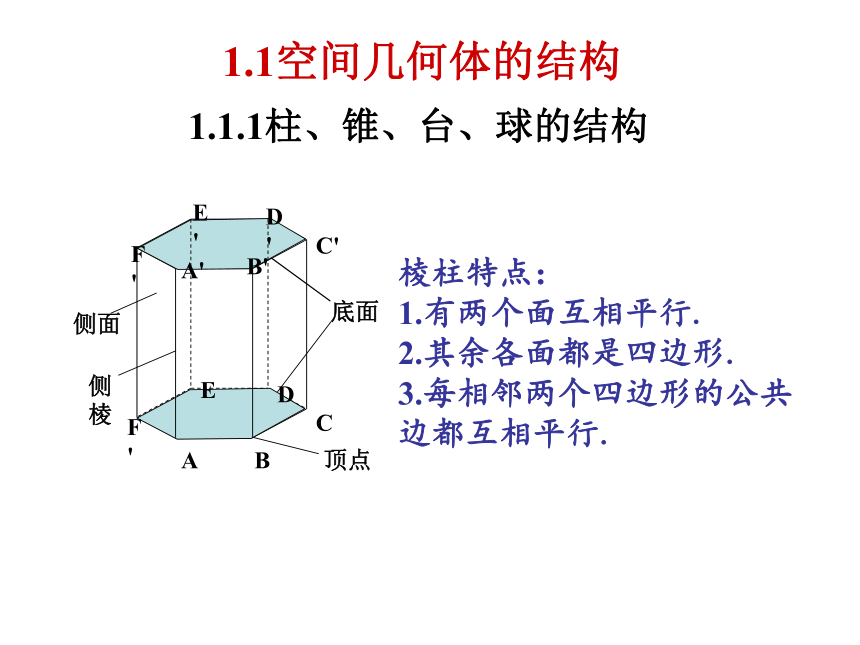
1.1.1柱、锥、台、球的结构
棱柱特点:
1.有两个面互相平行.
2.其余各面都是四边形.
3.每相邻两个四边形的公共边都互相平行.
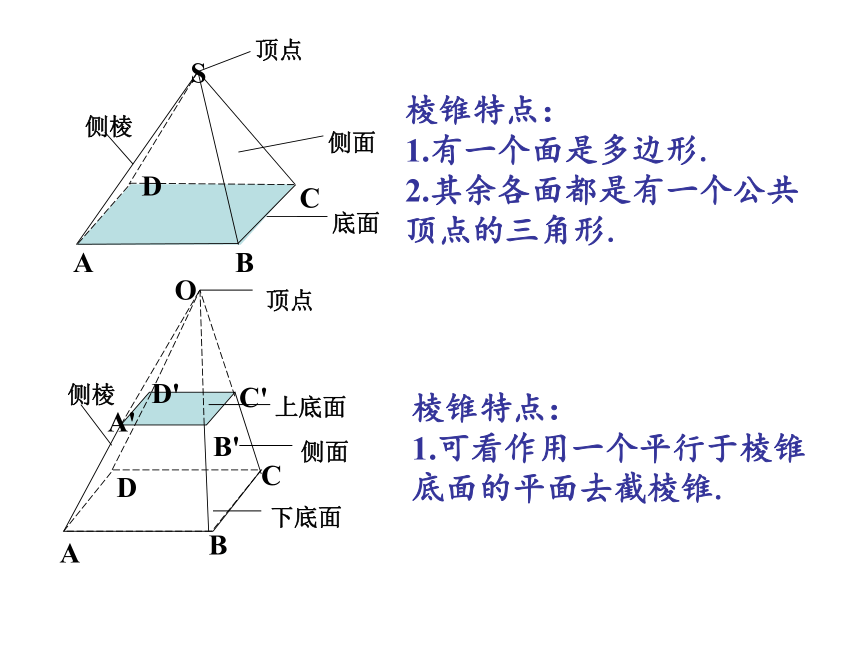
棱锥特点:
1.有一个面是多边形.
2.其余各面都是有一个公共顶点的三角形.
棱锥特点:
1.可看作用一个平行于棱锥底面的平面去截棱锥.
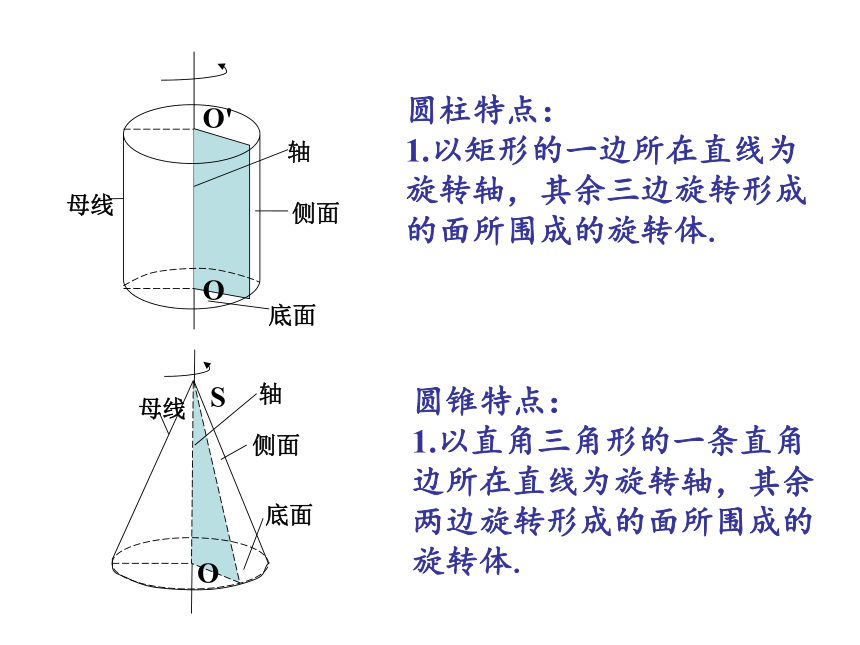
圆柱特点:
1.以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体.
圆锥特点:
1.以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体.
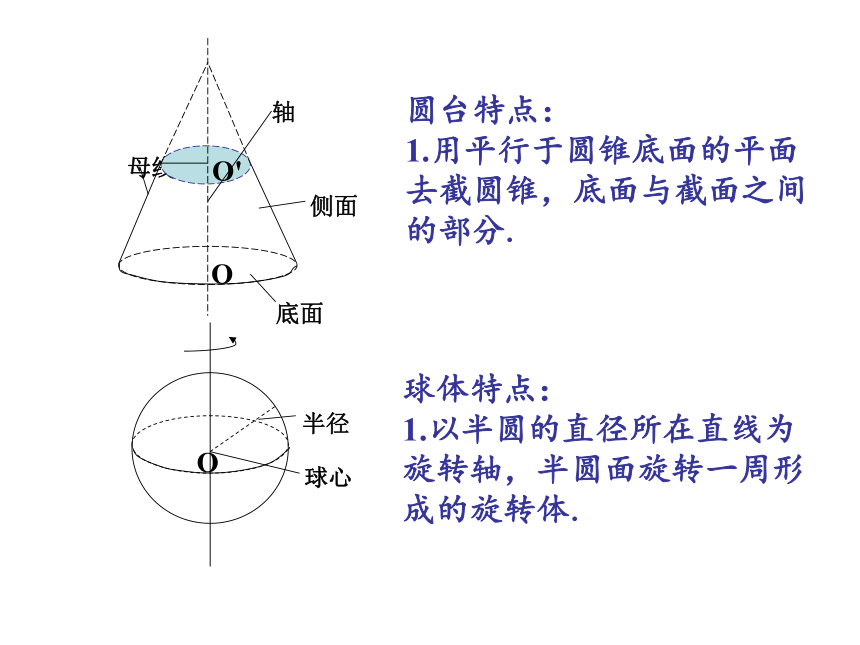
圆台特点:
1.用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分.
球体特点:
1.以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体.
回想转化的条件各是什么?
1.1.2简单组合体的结构特征
简单组合体的构成有两种基本形式
由简单几何体拼接而成.
简单几何体截去或挖去一部分而成.
1.2空间几何题的三视图和直观图
1.2.1中心投影与平行投影
投影
中心投影(投射线交于一点)
平行投影
正投影
斜投影
(投影线平行,且不正对投影面)
(投影线平行,且正对投影面)
1.2.2 空间几何体的三视图
三视图(根据平行投影得到的)
主视图——从正面看到的图
侧视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:主视图 侧视图
俯视图
大小:长对正,高平齐,宽相等.
常见几何体的三视图
几何体 正视图 侧视图 俯视图
·
常见几何体的三视图
几何体 正视图 侧视图 俯视图
1.2.3空间几何体的直观图
空间几何体的直观图通常是在平行投影下画的空间图形.
1、画轴
2、画底面
3、成图
确定平行线段
确定线段长度
画平面几何体的基本步骤:
1、画轴
2、画底面
3、画侧棱
4、成图
确定平行线段
确定线段长度
画空间几何体的基本步骤:
1.3空间几何体的表面积与体积
1.3.1柱体、椎体、台体、球体的表面积与体积
柱体、椎体、台体的表面积
柱体、椎体、台体的体积
1.3.2球的体积和表面积
半径是R的球的体积:
半径是R的球的表面积:
高考热点
1. 柱体、椎体、台体、球体的定义.
2. 简单几何体的三视图的画法.
3.体积问题几乎是每年必考,要能够应用体积公式解决一些问题.
本章易错点
1. 有两个面互相平行,其余各面都是平行四边形的几何体不一定是棱柱.要用棱柱定义判断.
2.画三视图时要注意长对正,高平齐,宽相等,并且能看到的地方用实线表示,不能看到的地方用虚线表示.
第一章 空间几何体
1.1 空间几何体的结构
1.2 空间几何体的三视图和直观图
1.3 空间几何体的表面积和体积
学法指导
1. 有两个面互相平行,其余各面都是平行四边形的几何体不一定是棱柱.要用棱柱定义判断.
2. 圆柱可以由矩形旋转得到,圆锥可以有直角三角形旋转得到,圆台直角梯形旋转得到.
3. 棱台、圆台可看作是棱锥、圆锥由平面截去一部分所得,所以棱台、圆台的问题常转化为棱锥、圆锥.
4. 画空间几何体的三视图时注意长对正,高平齐,宽相等.
5. 画空间几何体的直观图时注意x,y轴相交成45°,平行x轴的线段的长度保持不变.平行y轴的线段的长度变为原来的一半.
要点总结
1.1空间几何体的结构
1.1.1柱、锥、台、球的结构
棱柱特点:
1.有两个面互相平行.
2.其余各面都是四边形.
3.每相邻两个四边形的公共边都互相平行.
棱锥特点:
1.有一个面是多边形.
2.其余各面都是有一个公共顶点的三角形.
棱锥特点:
1.可看作用一个平行于棱锥底面的平面去截棱锥.
圆柱特点:
1.以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体.
圆锥特点:
1.以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体.
圆台特点:
1.用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分.
球体特点:
1.以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体.
回想转化的条件各是什么?
1.1.2简单组合体的结构特征
简单组合体的构成有两种基本形式
由简单几何体拼接而成.
简单几何体截去或挖去一部分而成.
1.2空间几何题的三视图和直观图
1.2.1中心投影与平行投影
投影
中心投影(投射线交于一点)
平行投影
正投影
斜投影
(投影线平行,且不正对投影面)
(投影线平行,且正对投影面)
1.2.2 空间几何体的三视图
三视图(根据平行投影得到的)
主视图——从正面看到的图
侧视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:主视图 侧视图
俯视图
大小:长对正,高平齐,宽相等.
常见几何体的三视图
几何体 正视图 侧视图 俯视图
·
常见几何体的三视图
几何体 正视图 侧视图 俯视图
1.2.3空间几何体的直观图
空间几何体的直观图通常是在平行投影下画的空间图形.
1、画轴
2、画底面
3、成图
确定平行线段
确定线段长度
画平面几何体的基本步骤:
1、画轴
2、画底面
3、画侧棱
4、成图
确定平行线段
确定线段长度
画空间几何体的基本步骤:
1.3空间几何体的表面积与体积
1.3.1柱体、椎体、台体、球体的表面积与体积
柱体、椎体、台体的表面积
柱体、椎体、台体的体积
1.3.2球的体积和表面积
半径是R的球的体积:
半径是R的球的表面积:
高考热点
1. 柱体、椎体、台体、球体的定义.
2. 简单几何体的三视图的画法.
3.体积问题几乎是每年必考,要能够应用体积公式解决一些问题.
本章易错点
1. 有两个面互相平行,其余各面都是平行四边形的几何体不一定是棱柱.要用棱柱定义判断.
2.画三视图时要注意长对正,高平齐,宽相等,并且能看到的地方用实线表示,不能看到的地方用虚线表示.
