必修2 第4章 圆与方程 单元复习(共16张PPT)
文档属性
| 名称 | 必修2 第4章 圆与方程 单元复习(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 514.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 13:13:50 | ||
图片预览





文档简介
(共16张PPT)
第四章 圆与方程
4.1圆的方程
4.2直线、圆的位置关系
4.3空间直角坐标系
①若知道或涉及圆心和半径,我们一般采用圆的标准方程较简单.
1.要学会根据题目条件,恰当选择圆方程形式:
②若已知三点求圆的方程,我们常常采用圆的一般方程用待定系数法求解.
2. 直线与圆的位置关系可以通过公共点的个数来来判断,但圆与圆的位置关系不能只通过公共点的个数来判断.
4.1圆的方程
4.1.1圆的标准方程
1.圆的基本要素:圆心位置、半径.
4.判断点与直线的位置关系:点到圆心的距离与半径的大小关系.
1.圆的一般方程:
2.圆的一般方程与圆的标准方程的联系:
4.1.2圆的一般方程
3.配方法求解:给出圆的一般方程,如何求圆心和半径.
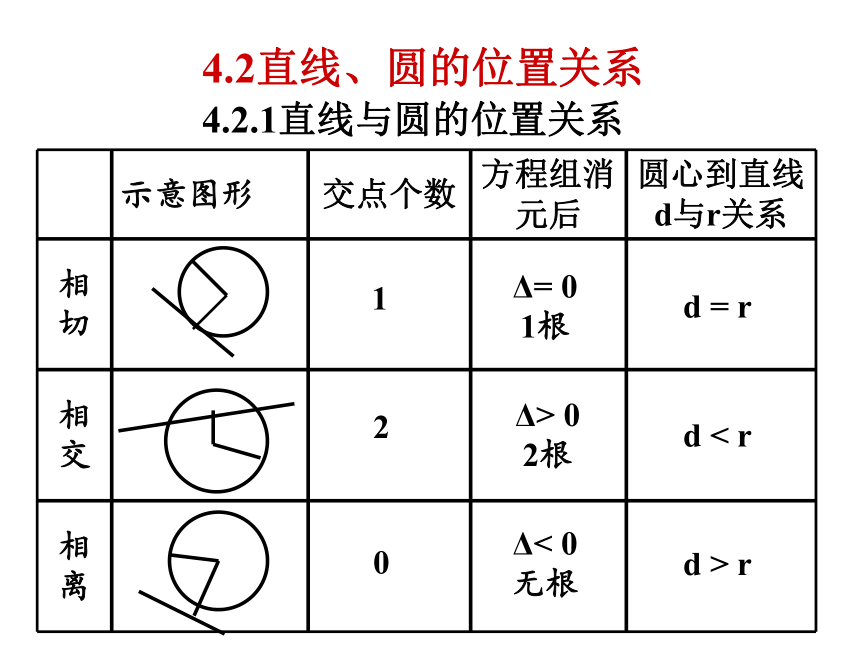
4.2直线、圆的位置关系
4.2.1直线与圆的位置关系
1
Δ= 0
1根
d = r
2
Δ> 0
2根
d < r
0
Δ< 0
无根
d > r
示意图形 交点个数 方程组消元后 圆心到直线d与r关系
相切
相交
相离
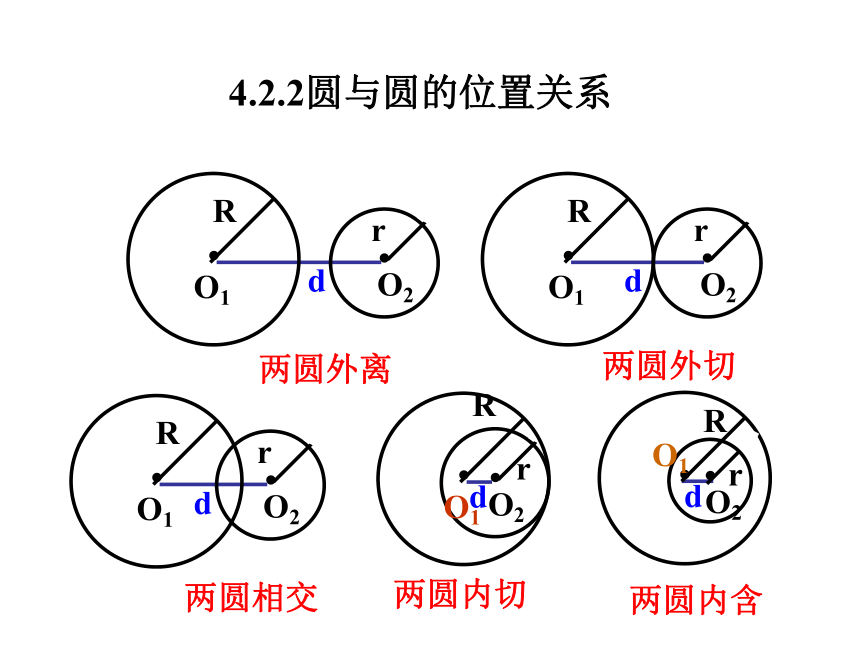
4.2.2圆与圆的位置关系
判断两圆的位置关系的两种方法:
1.根据圆心距与半径和之间的大小关系.
若d<|R-r|,则两圆内含;
若d=|R-r|,则两圆内切;
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离.
2.联立两圆方程,看截得解得个数.
4.2.3直线与圆的方程的应用
坐标法解决平面几何问题的“三步曲”
第一步:建系,几何问题代数化;
第二步:解决代数问题;
第三步:还原结论.
4.3空间直角坐标系
4.3.1空间直角坐标系
右手坐标系
点在空间直角坐标系中的坐标
4.3.2空间两点间的距离公式
2.几何问题转化为代数问题求解的思想.
1.用圆的标准方程和一般方程解决问题.
2.直线与圆的位置关系,及圆与圆位置关系的判定.
3.空间两点间距离公式的应用.
3.建立直角坐标系,满足建系规则才能建立右手坐标系.
2.判断圆与圆的位置关系时,不能只看交点个数,两圆有一个公共点,可能是外切,也可能是内切;
两圆没有公共点,可能是外离,也可能是内含.
第四章 圆与方程
4.1圆的方程
4.2直线、圆的位置关系
4.3空间直角坐标系
①若知道或涉及圆心和半径,我们一般采用圆的标准方程较简单.
1.要学会根据题目条件,恰当选择圆方程形式:
②若已知三点求圆的方程,我们常常采用圆的一般方程用待定系数法求解.
2. 直线与圆的位置关系可以通过公共点的个数来来判断,但圆与圆的位置关系不能只通过公共点的个数来判断.
4.1圆的方程
4.1.1圆的标准方程
1.圆的基本要素:圆心位置、半径.
4.判断点与直线的位置关系:点到圆心的距离与半径的大小关系.
1.圆的一般方程:
2.圆的一般方程与圆的标准方程的联系:
4.1.2圆的一般方程
3.配方法求解:给出圆的一般方程,如何求圆心和半径.
4.2直线、圆的位置关系
4.2.1直线与圆的位置关系
1
Δ= 0
1根
d = r
2
Δ> 0
2根
d < r
0
Δ< 0
无根
d > r
示意图形 交点个数 方程组消元后 圆心到直线d与r关系
相切
相交
相离
4.2.2圆与圆的位置关系
判断两圆的位置关系的两种方法:
1.根据圆心距与半径和之间的大小关系.
若d<|R-r|,则两圆内含;
若d=|R-r|,则两圆内切;
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离.
2.联立两圆方程,看截得解得个数.
4.2.3直线与圆的方程的应用
坐标法解决平面几何问题的“三步曲”
第一步:建系,几何问题代数化;
第二步:解决代数问题;
第三步:还原结论.
4.3空间直角坐标系
4.3.1空间直角坐标系
右手坐标系
点在空间直角坐标系中的坐标
4.3.2空间两点间的距离公式
2.几何问题转化为代数问题求解的思想.
1.用圆的标准方程和一般方程解决问题.
2.直线与圆的位置关系,及圆与圆位置关系的判定.
3.空间两点间距离公式的应用.
3.建立直角坐标系,满足建系规则才能建立右手坐标系.
2.判断圆与圆的位置关系时,不能只看交点个数,两圆有一个公共点,可能是外切,也可能是内切;
两圆没有公共点,可能是外离,也可能是内含.
