北师大版九年级数学下册第三章 圆达标检测题(含答案)
文档属性
| 名称 | 北师大版九年级数学下册第三章 圆达标检测题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-30 00:00:00 | ||
图片预览



文档简介
北师大版九年级数学下册 第三章 达标检测题
(时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
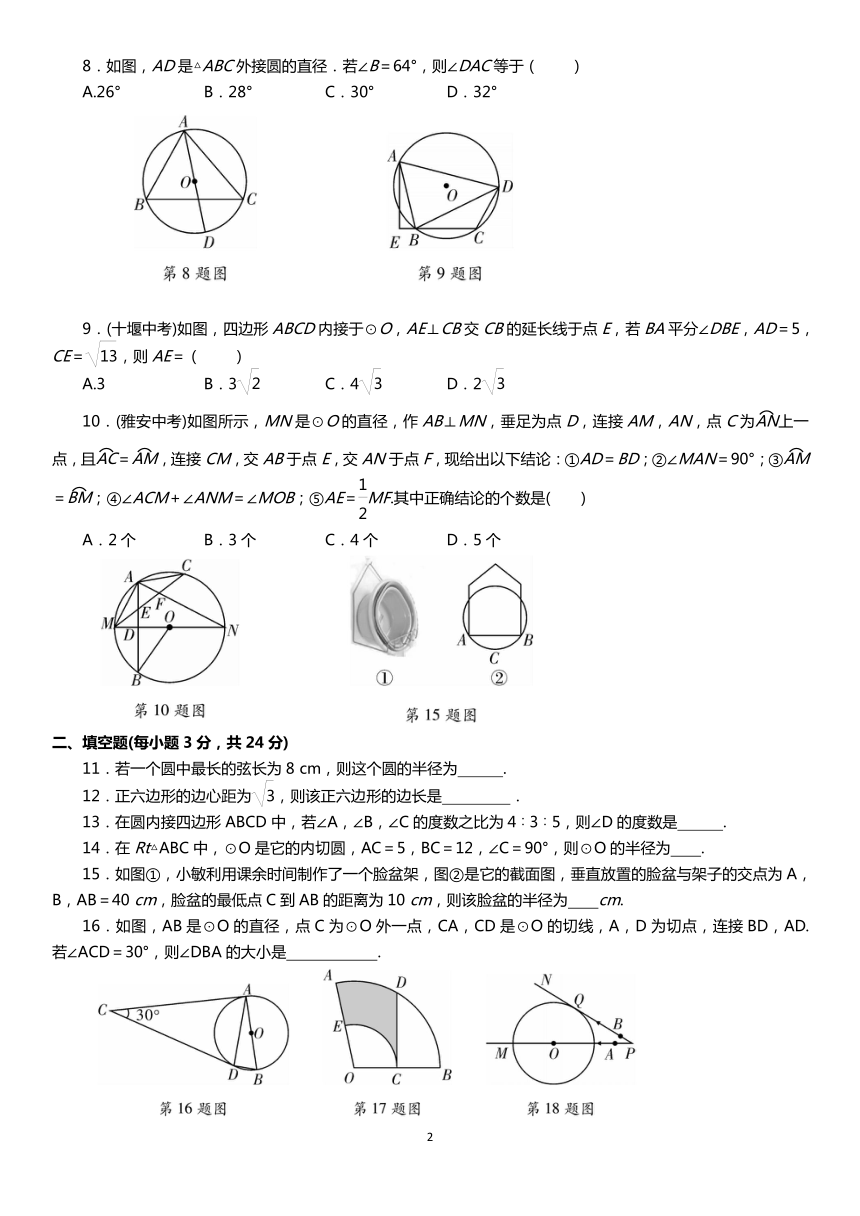
1.下列说法中,正确的是( )
A.两点确定一个圆
B.度数相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2.如图,在⊙O中,=,∠AOB=40°,则∠COD的度数为( )
A.20° B.40° C.50° D.60°
3.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径OC为5 m,则水面宽AB为( )
A.4 m B.5 m C.6 m D.8 m
4.如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
A.30° B.35° C.45° D.60°
5.已知⊙O的半径是5 cm,点O到直线l的距离OP=3 cm,Q为l上一点,且PQ=4.2 cm,则点Q( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.不确定
6.如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A.40° B.50° C.60° D.70°
如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,AB=8,则的长为( )
A.π B.π C.2π D.π
8.如图,AD是△ABC外接圆的直径.若∠B=64°,则∠DAC等于( )
A.26° B.28° C.30° D.32°
9.(十堰中考)如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE=( )
A.3 B.3 C.4 D.2
10.(雅安中考)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共24分)
11.若一个圆中最长的弦长为8 cm,则这个圆的半径为 .
12.正六边形的边心距为,则该正六边形的边长是 .
13.在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是 .
14.在Rt△ABC中,⊙O是它的内切圆,AC=5,BC=12,∠C=90°,则⊙O的半径为 .
15.如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为 cm.
16.如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是 .
17.如图,在扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交于点D,以OC为半径的交OA于点E,则图中阴影部分的面积是 .
18.如图,已知⊙O的半径为9 cm,射线PM经过点O,OP=15 cm,射线PN与⊙O相切于点Q,动点A自P点以 cm/s的速度沿射线PM方向运动,同时动点B也自P点以2 cm/s的速度沿射线PN方向运动,则它们从点P出发 后,AB所在直线与⊙O相切.
三、解答题(共66分)
19.(8分)已知等腰△ABC.
(1)用直尺和圆规作△ABC的外接圆;
(2)设△ABC的外接圆的圆心为点O.若∠BOC=128°,求∠BAC的度数.
20.(10分)已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
求证:(1)△ABC是等边三角形;
(2).
21.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
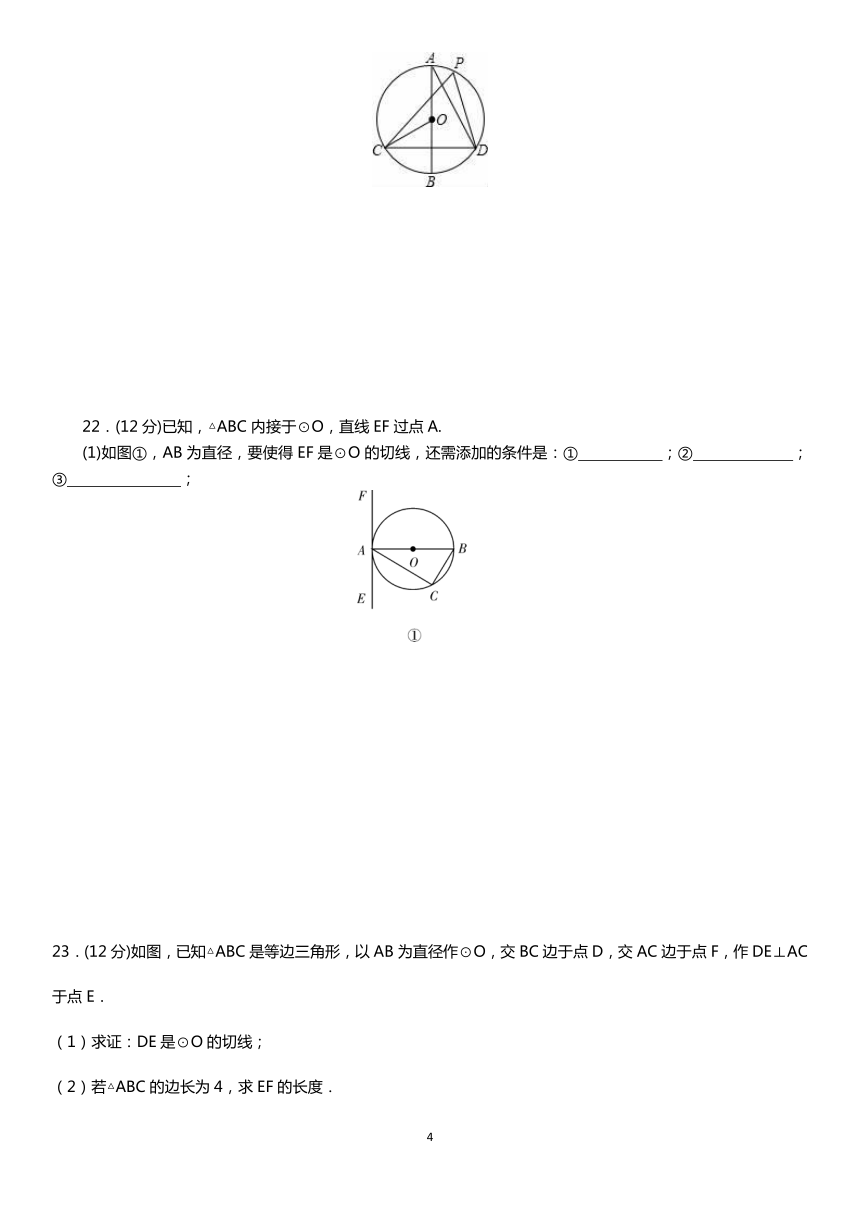
22.(12分)已知,△ABC内接于⊙O,直线EF过点A.
(1)如图①,AB为直径,要使得EF是⊙O的切线,还需添加的条件是:① ;② ;③ ;
23.(12分)如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
24.(14分)如图①所示,已知AB为⊙O的直径,∠A=∠B=90°,DE与⊙O相切于点E,⊙O的半径为,AD=2.
(1)求BC的长;
(2)如图②所示,延长AE交BC的延长线于G点,求EG的长.
参考答案
一、选择题(每小题3分,共30分)
1.下列说法中,正确的是( C )
A.两点确定一个圆
B.度数相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2.如图,在⊙O中,=,∠AOB=40°,则∠COD的度数为( B )
A.20° B.40° C.50° D.60°
3.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径OC为5 m,则水面宽AB为( D )
A.4 m B.5 m C.6 m D.8 m
4.如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( A )
A.30° B.35° C.45° D.60°
5.已知⊙O的半径是5 cm,点O到直线l的距离OP=3 cm,Q为l上一点,且PQ=4.2 cm,则点Q( C )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.不确定
6.如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( A )
A.40° B.50° C.60° D.70°
如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,AB=8,则的长为( D )
A.π B.π C.2π D.π
8.如图,AD是△ABC外接圆的直径.若∠B=64°,则∠DAC等于( A )
A.26° B.28° C.30° D.32°
9.(十堰中考)如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE=( D )
A.3 B.3 C.4 D.2
10.(雅安中考)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是( D )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共24分)
11.若一个圆中最长的弦长为8 cm,则这个圆的半径为 4 cm .
12.正六边形的边心距为,则该正六边形的边长是__2__.
13.在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是 120° .
14.在Rt△ABC中,⊙O是它的内切圆,AC=5,BC=12,∠C=90°,则⊙O的半径为 2 .
15.如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为 25 cm.
16.如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是 75° .
17.如图,在扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交于点D,以OC为半径的交OA于点E,则图中阴影部分的面积是 6π+18 .
18.如图,已知⊙O的半径为9 cm,射线PM经过点O,OP=15 cm,射线PN与⊙O相切于点Q,动点A自P点以 cm/s的速度沿射线PM方向运动,同时动点B也自P点以2 cm/s的速度沿射线PN方向运动,则它们从点P出发 1.5 s或10.5 s 后,AB所在直线与⊙O相切.
三、解答题(共66分)
19.(8分)如图,已知等腰△ABC.
(1)用直尺和圆规作△ABC的外接圆;
(2)设△ABC的外接圆的圆心为点O.若∠BOC=128°,求∠BAC的度数.
解:(1)如图所示.
(2)在优弧BC上任取一点D,连接BD,CD.
∵∠BOC=128°,∴∠BDC=∠BOC=64°.
∴∠BAC=180°-∠BDC=116°.
20.(10分)已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
求证:(1)△ABC是等边三角形;
(2).
【解答】证明:(1)连接OD,得OD∥AC;
∴∠BDO=∠A;
又OB=OD,
∴∠OBD=∠ODB;
∴∠OBD=∠A;
∴BC=AC;
又∵AB=AC,
∴△ABC是等边三角形;
(2)如上图,连接CD,则CD⊥AB;
∴D是AB中点;
∵AE=AD=AB,
∴EC=3AE;
∴AE=CE.
21.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
【解答】(1)证明:连接OD,
∵AB是直径,AB⊥CD,
∴.
∴∠COB=∠DOB=∠COD.
又∵∠CPD=∠COD,
∴∠CPD=∠COB.
(2)解:∠CP′D+∠COB=180°.
理由如下:连接OD,
∵∠CPD+∠CP′D=180°,∠COB=∠DOB=∠COD,
又∵∠CPD=∠COD,
∴∠COB=∠CPD,
∴∠CP′D+∠COB=180°.
22.(12分)已知,△ABC内接于⊙O,直线EF过点A.
(1)如图①,AB为直径,要使得EF是⊙O的切线,还需添加的条件是:① ∠ABC=∠EAC;② ∠FAB=∠C ;③ ∠BAE=90° ;
(2)如图②,AB为非直径弦,且∠CAE=∠B,求证:EF为⊙O的切线.
证明:连接AO并延长交圆上于点M,连接CM,
∵∠M=∠B,∠CAE=∠B,∴∠M=∠CAE.
∵AM为直径,∴∠ACM=90°,∴∠BAC+∠BAM+∠M=90°,
∴∠BAC+∠BAM+∠CAE=90°,∴OA⊥EF,∴EF为⊙O的切线.
23.(12分)如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
【解答】(1)证明:如图1,连接OD,
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:如图2,连接AD,BF,
∵AB为⊙O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴,.
∵∠EDC=30°,
∴.
∴FE=FC﹣EC=1.
24.(14分)如图①所示,已知AB为⊙O的直径,∠A=∠B=90°,DE与⊙O相切于点E,⊙O的半径为,AD=2.
(1)求BC的长;
(2)如图②所示,延长AE交BC的延长线于G点,求EG的长.
题图 答图
解:(1)如图,过点D作DF⊥BC于点F,∵AB为⊙O的直径,∠A=∠B=90°,∴四边形ABFD是矩形,AD与BC是⊙O的切线,∴DF=AB=2,BF=AD=2.∵DE与⊙O相切,
∴DE=AD=2,CE=BC,
设BC=x,则CF=BC-BF=x-2,
DC=DE+CE=2+x.
在Rt△DCF中,
由勾股定理得DC2=CF2+DF2,
∴(2+x)2=(x-2)2+(2)2,
解得x=,即BC=.
(2)∵AB为⊙O的直径,∠DAB=∠B=90°,∴AD∥BC,
∴△ADE∽△GCE,∴AD∶CG=DE∶CE,AE∶EG=AD∶CG.
又易知AD=DE=2,∴CG=CE=BC=,∴BG=BC+CG=5,
∴AE∶EG=4∶5,在Rt△ABG中,
由勾股定理得AG==3,∴EG=AG=.
(时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列说法中,正确的是( )
A.两点确定一个圆
B.度数相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2.如图,在⊙O中,=,∠AOB=40°,则∠COD的度数为( )
A.20° B.40° C.50° D.60°
3.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径OC为5 m,则水面宽AB为( )
A.4 m B.5 m C.6 m D.8 m
4.如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
A.30° B.35° C.45° D.60°
5.已知⊙O的半径是5 cm,点O到直线l的距离OP=3 cm,Q为l上一点,且PQ=4.2 cm,则点Q( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.不确定
6.如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A.40° B.50° C.60° D.70°
如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,AB=8,则的长为( )
A.π B.π C.2π D.π
8.如图,AD是△ABC外接圆的直径.若∠B=64°,则∠DAC等于( )
A.26° B.28° C.30° D.32°
9.(十堰中考)如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE=( )
A.3 B.3 C.4 D.2
10.(雅安中考)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共24分)
11.若一个圆中最长的弦长为8 cm,则这个圆的半径为 .
12.正六边形的边心距为,则该正六边形的边长是 .
13.在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是 .
14.在Rt△ABC中,⊙O是它的内切圆,AC=5,BC=12,∠C=90°,则⊙O的半径为 .
15.如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为 cm.
16.如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是 .
17.如图,在扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交于点D,以OC为半径的交OA于点E,则图中阴影部分的面积是 .
18.如图,已知⊙O的半径为9 cm,射线PM经过点O,OP=15 cm,射线PN与⊙O相切于点Q,动点A自P点以 cm/s的速度沿射线PM方向运动,同时动点B也自P点以2 cm/s的速度沿射线PN方向运动,则它们从点P出发 后,AB所在直线与⊙O相切.
三、解答题(共66分)
19.(8分)已知等腰△ABC.
(1)用直尺和圆规作△ABC的外接圆;
(2)设△ABC的外接圆的圆心为点O.若∠BOC=128°,求∠BAC的度数.
20.(10分)已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
求证:(1)△ABC是等边三角形;
(2).
21.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
22.(12分)已知,△ABC内接于⊙O,直线EF过点A.
(1)如图①,AB为直径,要使得EF是⊙O的切线,还需添加的条件是:① ;② ;③ ;
23.(12分)如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
24.(14分)如图①所示,已知AB为⊙O的直径,∠A=∠B=90°,DE与⊙O相切于点E,⊙O的半径为,AD=2.
(1)求BC的长;
(2)如图②所示,延长AE交BC的延长线于G点,求EG的长.
参考答案
一、选择题(每小题3分,共30分)
1.下列说法中,正确的是( C )
A.两点确定一个圆
B.度数相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2.如图,在⊙O中,=,∠AOB=40°,则∠COD的度数为( B )
A.20° B.40° C.50° D.60°
3.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径OC为5 m,则水面宽AB为( D )
A.4 m B.5 m C.6 m D.8 m
4.如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( A )
A.30° B.35° C.45° D.60°
5.已知⊙O的半径是5 cm,点O到直线l的距离OP=3 cm,Q为l上一点,且PQ=4.2 cm,则点Q( C )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.不确定
6.如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( A )
A.40° B.50° C.60° D.70°
如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,AB=8,则的长为( D )
A.π B.π C.2π D.π
8.如图,AD是△ABC外接圆的直径.若∠B=64°,则∠DAC等于( A )
A.26° B.28° C.30° D.32°
9.(十堰中考)如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE=( D )
A.3 B.3 C.4 D.2
10.(雅安中考)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是( D )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共24分)
11.若一个圆中最长的弦长为8 cm,则这个圆的半径为 4 cm .
12.正六边形的边心距为,则该正六边形的边长是__2__.
13.在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是 120° .
14.在Rt△ABC中,⊙O是它的内切圆,AC=5,BC=12,∠C=90°,则⊙O的半径为 2 .
15.如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为 25 cm.
16.如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是 75° .
17.如图,在扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交于点D,以OC为半径的交OA于点E,则图中阴影部分的面积是 6π+18 .
18.如图,已知⊙O的半径为9 cm,射线PM经过点O,OP=15 cm,射线PN与⊙O相切于点Q,动点A自P点以 cm/s的速度沿射线PM方向运动,同时动点B也自P点以2 cm/s的速度沿射线PN方向运动,则它们从点P出发 1.5 s或10.5 s 后,AB所在直线与⊙O相切.
三、解答题(共66分)
19.(8分)如图,已知等腰△ABC.
(1)用直尺和圆规作△ABC的外接圆;
(2)设△ABC的外接圆的圆心为点O.若∠BOC=128°,求∠BAC的度数.
解:(1)如图所示.
(2)在优弧BC上任取一点D,连接BD,CD.
∵∠BOC=128°,∴∠BDC=∠BOC=64°.
∴∠BAC=180°-∠BDC=116°.
20.(10分)已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
求证:(1)△ABC是等边三角形;
(2).
【解答】证明:(1)连接OD,得OD∥AC;
∴∠BDO=∠A;
又OB=OD,
∴∠OBD=∠ODB;
∴∠OBD=∠A;
∴BC=AC;
又∵AB=AC,
∴△ABC是等边三角形;
(2)如上图,连接CD,则CD⊥AB;
∴D是AB中点;
∵AE=AD=AB,
∴EC=3AE;
∴AE=CE.
21.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
【解答】(1)证明:连接OD,
∵AB是直径,AB⊥CD,
∴.
∴∠COB=∠DOB=∠COD.
又∵∠CPD=∠COD,
∴∠CPD=∠COB.
(2)解:∠CP′D+∠COB=180°.
理由如下:连接OD,
∵∠CPD+∠CP′D=180°,∠COB=∠DOB=∠COD,
又∵∠CPD=∠COD,
∴∠COB=∠CPD,
∴∠CP′D+∠COB=180°.
22.(12分)已知,△ABC内接于⊙O,直线EF过点A.
(1)如图①,AB为直径,要使得EF是⊙O的切线,还需添加的条件是:① ∠ABC=∠EAC;② ∠FAB=∠C ;③ ∠BAE=90° ;
(2)如图②,AB为非直径弦,且∠CAE=∠B,求证:EF为⊙O的切线.
证明:连接AO并延长交圆上于点M,连接CM,
∵∠M=∠B,∠CAE=∠B,∴∠M=∠CAE.
∵AM为直径,∴∠ACM=90°,∴∠BAC+∠BAM+∠M=90°,
∴∠BAC+∠BAM+∠CAE=90°,∴OA⊥EF,∴EF为⊙O的切线.
23.(12分)如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
【解答】(1)证明:如图1,连接OD,
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:如图2,连接AD,BF,
∵AB为⊙O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴,.
∵∠EDC=30°,
∴.
∴FE=FC﹣EC=1.
24.(14分)如图①所示,已知AB为⊙O的直径,∠A=∠B=90°,DE与⊙O相切于点E,⊙O的半径为,AD=2.
(1)求BC的长;
(2)如图②所示,延长AE交BC的延长线于G点,求EG的长.
题图 答图
解:(1)如图,过点D作DF⊥BC于点F,∵AB为⊙O的直径,∠A=∠B=90°,∴四边形ABFD是矩形,AD与BC是⊙O的切线,∴DF=AB=2,BF=AD=2.∵DE与⊙O相切,
∴DE=AD=2,CE=BC,
设BC=x,则CF=BC-BF=x-2,
DC=DE+CE=2+x.
在Rt△DCF中,
由勾股定理得DC2=CF2+DF2,
∴(2+x)2=(x-2)2+(2)2,
解得x=,即BC=.
(2)∵AB为⊙O的直径,∠DAB=∠B=90°,∴AD∥BC,
∴△ADE∽△GCE,∴AD∶CG=DE∶CE,AE∶EG=AD∶CG.
又易知AD=DE=2,∴CG=CE=BC=,∴BG=BC+CG=5,
∴AE∶EG=4∶5,在Rt△ABG中,
由勾股定理得AG==3,∴EG=AG=.
