2.3.2 两个变量的线性关系 课件(共27张PPT)
文档属性
| 名称 | 2.3.2 两个变量的线性关系 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
导入新课
1. 变量之间的相互关系
两个变量之间的关系,可能是确定关系或非确定关系。当自变量却只一定,因变量的取值带有一定随机性时,两个变量之间的关系成为相关关系。相关关系是一种不确定性关系。
3. 通过收集大量的数据,进行统计,对数据分析,找出其中的规律,对其相关关系作出一定判断.
4. 由于变量之间相关关系的广泛性和不确定性,所以样本数据应较大和有代表性,才能对它们之间的关系作出正确的判断。
2. 前面我们学习了现实生活中存在许多相关关系:商品销售与广告、粮食生产与施肥量、人体的脂肪量与年龄等等的相关关系。
2.3.2 两个变量的线性关系
1.最小二乘法;
2.建立线性回归方程;
3.理解变量之间的相关关系。
知识与技能
教学目标
过程与方法
在解决统计问题的过程中,逐步体会用变量间相关关系,理解数形结合的数学思想和逻辑推理的数学方法。
情感态度与价值观
会用变量之间的相关关系解决一些简单的实际问题,认识统计的作用,能够辨证地理解数学知识与现实世界的联系。
重点
1.了解最小二乘法的思想;
2.根据给出的线性回归方程的系数公式建立线性回归方程,变量之间相关关系的理解。
教学重难点
回归思想的建立;
对回归直线与观测数据的关系的理解。
难点
在一次对人体脂肪含量和年龄的关系研究中,研究人员获得了一份样本数据:
根据上述数据,人体的脂肪含量与年龄之间有什么样的关系?
说明:各个年龄阶段的脂肪数据是这个年龄样本的平均数
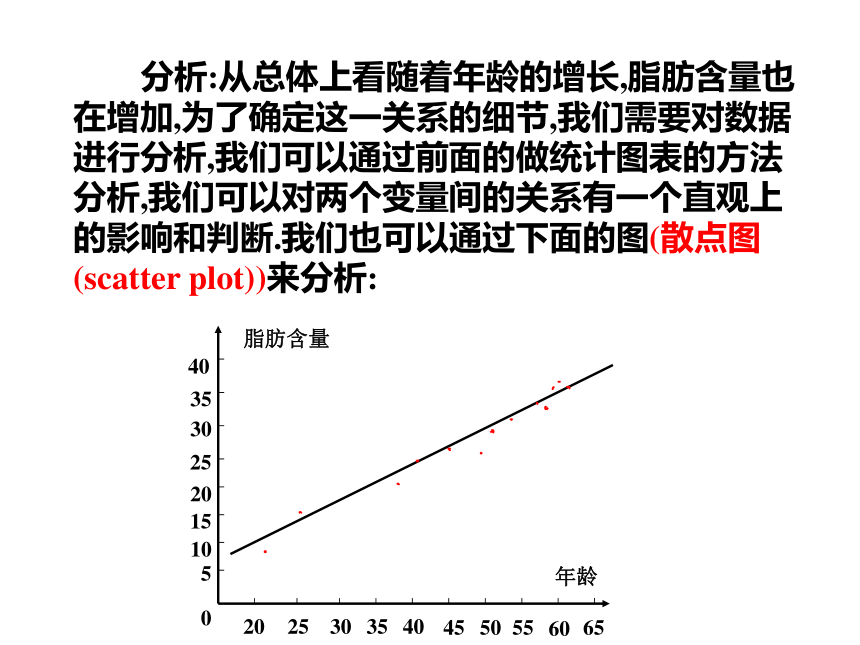
分析:从总体上看随着年龄的增长,脂肪含量也在增加,为了确定这一关系的细节,我们需要对数据进行分析,我们可以通过前面的做统计图表的方法分析,我们可以对两个变量间的关系有一个直观上的影响和判断.我们也可以通过下面的图(散点图(scatter plot))来分析:
20
25
30
35
40
45
50
55
60
65
年龄
脂肪含量
0
5
10
15
20
25
30
35
40
通过分析、观察可以看到:随着年龄的增长,人体脂肪含量越高,这表明两个变量之间的确存在一定的关系。
递增我们叫它们正相关
递减我们叫它们负相关
20
25
30
35
40
45
50
55
60
65
年龄
脂肪含量
0
5
10
15
20
25
30
35
40
知识要点
回归直线
从散点图可以看出:所有的点大致在一条直线附近波动,我们称这两个变量间存在线性相关关系,这条直线叫做回归直线(regression line) 。
如果可以求出这条直线的方程(回归方程),那么我们就可以比较清楚的了解年龄与体内脂肪含量的相关性.这条直线就可以作为两个变量具有线性相关关系的代表
怎样求线性回归方程呢?
想一想
1. 测量法:移动直线l使所有点到它的距离之和最小
方法
2.两点确定法:选取两点作直线,使其两边点个数一样
3.分组法:将点进行分组点,分别求其斜率和截距,求平均值
如何用你熟悉的数学知识来刻画“从整体上看各点与此直线距离最短”呢?
人们经过长期的实践与研究,已经找到了
计算回归方程的斜率与截距的一般公式:
最小二乘法。
知识要点
最小二乘法
即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。
最小二乘法的计算公式:
下表是某小卖部6天卖出热茶的杯数(y)与当天气温(x)的对比表:
(1)试用最小二乘法求出线性回归方程;
(2)如果某天的气温是-3℃,请预测这天可能会卖出热茶多少杯 ?
(1)作散点图如图所示
解:
由散点图知两个变量是线性相关的,计算各种数据如下表:
分步计算减少出错
于是:
则:
于是,线性回归方程为? y=57.557-1.648x
(2)由回归方程知,当某天的气温是-3℃时,卖出的热茶杯数为
57.557-1.648×(-3)≈63(杯)
课堂小结
1. 回归直线
从散点图可以看出:所有的点大致在一条直线附近波动,我们称这两个变量间存在线性相关关系,这条直线叫做回归直线(regression line) 。
2. 最小二乘法法
即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。
1.首先要作出数据的散点图,利用散点图观
察数据是否具有线性关系;
2.散点图呈现线性关系时,利用最小二乘公
式求出回归方程;
3.求出相应的解。
3. 最小二乘法法的步骤
1、对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图①;对变量u,v有观测数据(ui,vi)(i=1,2,….,10),得散点图②。由这两个散点图可以判断( )
针对性练习
C
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
解析:
本题主要考查两个变量的线性相关性,由图①可看出离散点分布在一条斜率为负的直线周围,所以变量x,y成负相关;而图②的离散点分布在一条斜率为正的直线周围,所以变量u,v成正相关。
1. 球的体积和球的半径具有( )
A. 函数关系 B. 相关关系
C. 不确定关系 D. 无任何关系
2. 下列两个变量之间的关系不是函数关系的是( )
角的度数和正弦值
B. 速度一定时,距离和时间的关系
C. 正方体的棱长和体积
D. 日照时间和水稻的亩产量
A
D
随堂练习
3.三点(3,10),(7,20),(11,24)的线性回归方程是 ( )
D
导入新课
1. 变量之间的相互关系
两个变量之间的关系,可能是确定关系或非确定关系。当自变量却只一定,因变量的取值带有一定随机性时,两个变量之间的关系成为相关关系。相关关系是一种不确定性关系。
3. 通过收集大量的数据,进行统计,对数据分析,找出其中的规律,对其相关关系作出一定判断.
4. 由于变量之间相关关系的广泛性和不确定性,所以样本数据应较大和有代表性,才能对它们之间的关系作出正确的判断。
2. 前面我们学习了现实生活中存在许多相关关系:商品销售与广告、粮食生产与施肥量、人体的脂肪量与年龄等等的相关关系。
2.3.2 两个变量的线性关系
1.最小二乘法;
2.建立线性回归方程;
3.理解变量之间的相关关系。
知识与技能
教学目标
过程与方法
在解决统计问题的过程中,逐步体会用变量间相关关系,理解数形结合的数学思想和逻辑推理的数学方法。
情感态度与价值观
会用变量之间的相关关系解决一些简单的实际问题,认识统计的作用,能够辨证地理解数学知识与现实世界的联系。
重点
1.了解最小二乘法的思想;
2.根据给出的线性回归方程的系数公式建立线性回归方程,变量之间相关关系的理解。
教学重难点
回归思想的建立;
对回归直线与观测数据的关系的理解。
难点
在一次对人体脂肪含量和年龄的关系研究中,研究人员获得了一份样本数据:
根据上述数据,人体的脂肪含量与年龄之间有什么样的关系?
说明:各个年龄阶段的脂肪数据是这个年龄样本的平均数
分析:从总体上看随着年龄的增长,脂肪含量也在增加,为了确定这一关系的细节,我们需要对数据进行分析,我们可以通过前面的做统计图表的方法分析,我们可以对两个变量间的关系有一个直观上的影响和判断.我们也可以通过下面的图(散点图(scatter plot))来分析:
20
25
30
35
40
45
50
55
60
65
年龄
脂肪含量
0
5
10
15
20
25
30
35
40
通过分析、观察可以看到:随着年龄的增长,人体脂肪含量越高,这表明两个变量之间的确存在一定的关系。
递增我们叫它们正相关
递减我们叫它们负相关
20
25
30
35
40
45
50
55
60
65
年龄
脂肪含量
0
5
10
15
20
25
30
35
40
知识要点
回归直线
从散点图可以看出:所有的点大致在一条直线附近波动,我们称这两个变量间存在线性相关关系,这条直线叫做回归直线(regression line) 。
如果可以求出这条直线的方程(回归方程),那么我们就可以比较清楚的了解年龄与体内脂肪含量的相关性.这条直线就可以作为两个变量具有线性相关关系的代表
怎样求线性回归方程呢?
想一想
1. 测量法:移动直线l使所有点到它的距离之和最小
方法
2.两点确定法:选取两点作直线,使其两边点个数一样
3.分组法:将点进行分组点,分别求其斜率和截距,求平均值
如何用你熟悉的数学知识来刻画“从整体上看各点与此直线距离最短”呢?
人们经过长期的实践与研究,已经找到了
计算回归方程的斜率与截距的一般公式:
最小二乘法。
知识要点
最小二乘法
即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。
最小二乘法的计算公式:
下表是某小卖部6天卖出热茶的杯数(y)与当天气温(x)的对比表:
(1)试用最小二乘法求出线性回归方程;
(2)如果某天的气温是-3℃,请预测这天可能会卖出热茶多少杯 ?
(1)作散点图如图所示
解:
由散点图知两个变量是线性相关的,计算各种数据如下表:
分步计算减少出错
于是:
则:
于是,线性回归方程为? y=57.557-1.648x
(2)由回归方程知,当某天的气温是-3℃时,卖出的热茶杯数为
57.557-1.648×(-3)≈63(杯)
课堂小结
1. 回归直线
从散点图可以看出:所有的点大致在一条直线附近波动,我们称这两个变量间存在线性相关关系,这条直线叫做回归直线(regression line) 。
2. 最小二乘法法
即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。
1.首先要作出数据的散点图,利用散点图观
察数据是否具有线性关系;
2.散点图呈现线性关系时,利用最小二乘公
式求出回归方程;
3.求出相应的解。
3. 最小二乘法法的步骤
1、对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图①;对变量u,v有观测数据(ui,vi)(i=1,2,….,10),得散点图②。由这两个散点图可以判断( )
针对性练习
C
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
解析:
本题主要考查两个变量的线性相关性,由图①可看出离散点分布在一条斜率为负的直线周围,所以变量x,y成负相关;而图②的离散点分布在一条斜率为正的直线周围,所以变量u,v成正相关。
1. 球的体积和球的半径具有( )
A. 函数关系 B. 相关关系
C. 不确定关系 D. 无任何关系
2. 下列两个变量之间的关系不是函数关系的是( )
角的度数和正弦值
B. 速度一定时,距离和时间的关系
C. 正方体的棱长和体积
D. 日照时间和水稻的亩产量
A
D
随堂练习
3.三点(3,10),(7,20),(11,24)的线性回归方程是 ( )
D
