北师大版八年级上册数学第七章平行线的证明回顾与思考导学案+课外拓展AB(无答案)
文档属性
| 名称 | 北师大版八年级上册数学第七章平行线的证明回顾与思考导学案+课外拓展AB(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 116.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-30 22:52:23 | ||
图片预览

文档简介
八年级数学(上)导学案
《第七章 回顾与思考2》导学案
【教学目标】
1.熟练掌握平行线的判定和性质定理的综合应用;
2. 运用三角形的内角和定理和外角定理,完成相关的证明和计算;
【教学重点】运用平行线的判定和性质定理以及内外角定理,熟练完成规范的演绎推理;
【教学难点】相关探究类题目的处理。
【教学方法】自主探究
【教学流程】
知识整理:
三角形内角和定理: 。
三角形外角定理: 。
(二) 新知探究:
探究活动一: 平行线的判定和性质定理的综合应用
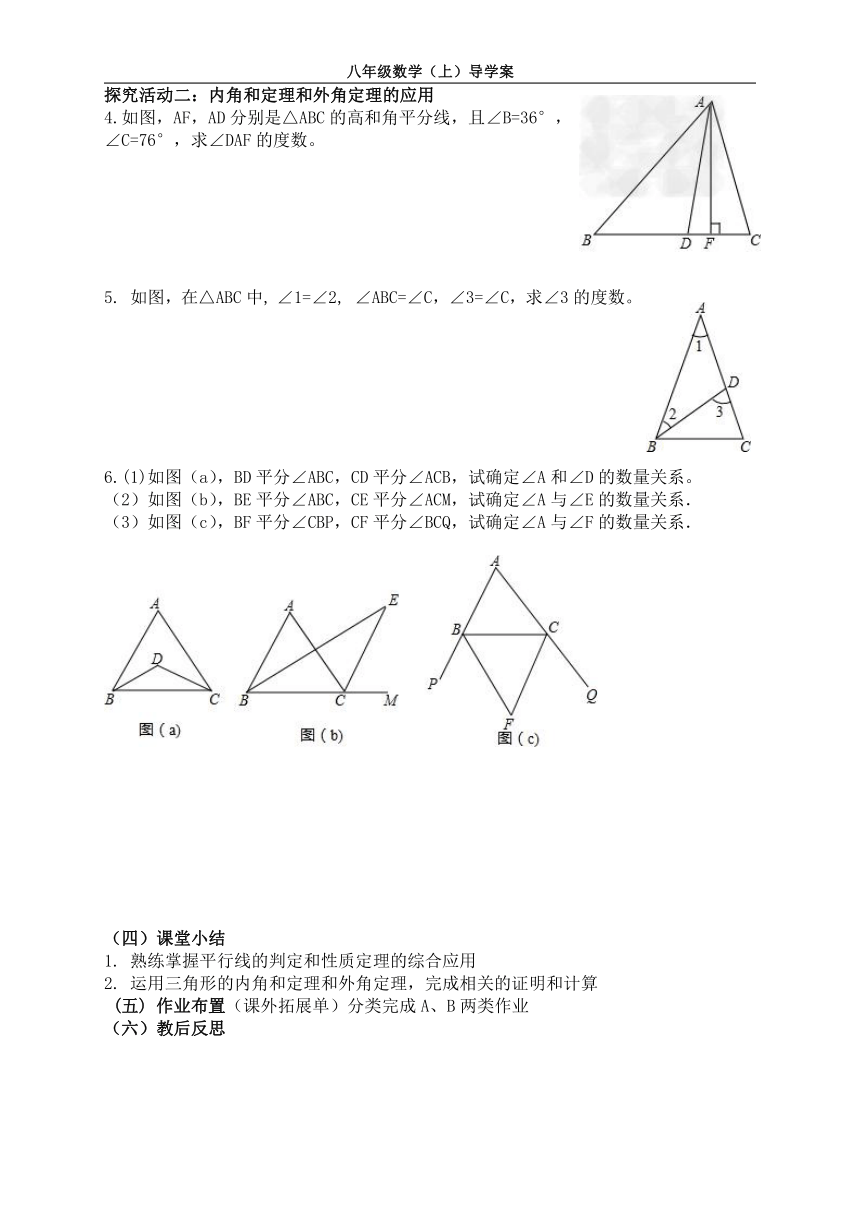
1.如图,在四边形ABCD中,∠A=104°-∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F,能辨认∠1=∠2吗?试说明理由.
2.如图,四边形ABCD中,∠C=70°,∠A=100°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN.若MF∥AD,FN∥DC,求∠D.
3.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.
探究活动二:内角和定理和外角定理的应用
4.如图,AF,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,求∠DAF的度数。
5. 如图,在△ABC中, ∠1=∠2, ∠ABC=∠C,∠3=∠C,求∠3的度数。
6.(1)如图(a),BD平分∠ABC,CD平分∠ACB,试确定∠A和∠D的数量关系。
(2)如图(b),BE平分∠ABC,CE平分∠ACM,试确定∠A与∠E的数量关系.
(3)如图(c),BF平分∠CBP,CF平分∠BCQ,试确定∠A与∠F的数量关系.
(四)课堂小结
1. 熟练掌握平行线的判定和性质定理的综合应用
2. 运用三角形的内角和定理和外角定理,完成相关的证明和计算
(五) 作业布置(课外拓展单)分类完成A、B两类作业
(六)教后反思
《7.2定义与证明2》课外巩固--评价单
姓名_________ 班级_________ 组名___________
A基础演练
1.如图,在△ABC中,AC⊥BC于C,DE⊥BC于E,FG⊥AB于G,∠1=∠2,求证:∠2与∠3互余。
2. 如图,在△ABC中,∠A:∠ABC:∠ACB=3:4:5,BD、CE分别是边AC、AB上的高,BD、CE相交于点H,求∠BHC的度数。
3.如图,在△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,求∠BDC的度数.
B能力提升(在背面)
4.如图,将三角形纸片ABC沿DE折叠,使点A落在A ' 处的位置,
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是______.
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
教师评价:
《第七章 回顾与思考2》导学案
【教学目标】
1.熟练掌握平行线的判定和性质定理的综合应用;
2. 运用三角形的内角和定理和外角定理,完成相关的证明和计算;
【教学重点】运用平行线的判定和性质定理以及内外角定理,熟练完成规范的演绎推理;
【教学难点】相关探究类题目的处理。
【教学方法】自主探究
【教学流程】
知识整理:
三角形内角和定理: 。
三角形外角定理: 。
(二) 新知探究:
探究活动一: 平行线的判定和性质定理的综合应用
1.如图,在四边形ABCD中,∠A=104°-∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F,能辨认∠1=∠2吗?试说明理由.
2.如图,四边形ABCD中,∠C=70°,∠A=100°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN.若MF∥AD,FN∥DC,求∠D.
3.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB,∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.
探究活动二:内角和定理和外角定理的应用
4.如图,AF,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,求∠DAF的度数。
5. 如图,在△ABC中, ∠1=∠2, ∠ABC=∠C,∠3=∠C,求∠3的度数。
6.(1)如图(a),BD平分∠ABC,CD平分∠ACB,试确定∠A和∠D的数量关系。
(2)如图(b),BE平分∠ABC,CE平分∠ACM,试确定∠A与∠E的数量关系.
(3)如图(c),BF平分∠CBP,CF平分∠BCQ,试确定∠A与∠F的数量关系.
(四)课堂小结
1. 熟练掌握平行线的判定和性质定理的综合应用
2. 运用三角形的内角和定理和外角定理,完成相关的证明和计算
(五) 作业布置(课外拓展单)分类完成A、B两类作业
(六)教后反思
《7.2定义与证明2》课外巩固--评价单
姓名_________ 班级_________ 组名___________
A基础演练
1.如图,在△ABC中,AC⊥BC于C,DE⊥BC于E,FG⊥AB于G,∠1=∠2,求证:∠2与∠3互余。
2. 如图,在△ABC中,∠A:∠ABC:∠ACB=3:4:5,BD、CE分别是边AC、AB上的高,BD、CE相交于点H,求∠BHC的度数。
3.如图,在△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,求∠BDC的度数.
B能力提升(在背面)
4.如图,将三角形纸片ABC沿DE折叠,使点A落在A ' 处的位置,
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是______.
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
教师评价:
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
