5.2.2 平行线的判定课件
图片预览








文档简介
(共26张PPT)
人教版 七年级数学下
5.2.2平行线的判定
学习目标
1.掌握平行线的三种判定方法,会运用判定方法来判断两条直线是否平行;(重点)
2.能够根据平行线的判定方法进行简单的推理.(难点)
回顾旧知
问题1 在同一平面内,两条不重合的直线的位置关系有哪几种?
问题2 怎样的两条直线平行?
问题3 上节课你学了平行线的哪些内容?
相交(包括垂直)和平行两种.
在同一平面内,不相交的两条直线平行.
2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
1.经过直线外一点,有且只有一条直线与已知直线平行.
回顾旧知
思考: 根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否相交来判定是否平行,那么有没有其他判定方法呢?
合作探究---平行线的判定
●
一、放
二、靠
三、移
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
合作探究---平行线的判定
b
A
2
1
a
B
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
同位角
平行
合作探究---平行线的判定
(3)将其最初和最终的两种特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(4) 由上面的操作过程,你能发现判定两直线平行的方法吗?
合作探究---平行线的判定
A
B
C
D
E
F
H
G
1
2
平行线的判定方法1:
两条直线被第三条直线所截,如果同位角相等,
那么这两条直线平行。
简单说成:
同位角相等,两直线平行。
(任何一对)
∵ ∠1=∠2(已知)
∴ AB∥CD(同位角相等,两直线平行)
几何语言:
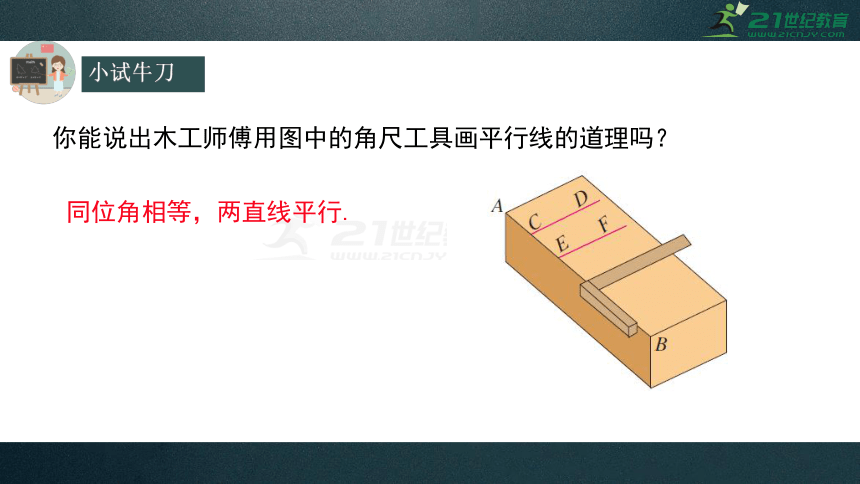
小试牛刀
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
同位角相等,两直线平行.
合作探究---平行线的判定
3
证明:∵ ∠1=∠2 (已知)
∴ AB∥CD
2
A
B
C
D
E
F
1
【问题1】如图,已知∠1=∠2,求证:AB∥CD.
∠1=∠3 (对顶角相等)
∴∠2=∠3 (等量代换)
(同位角相等,两直线平行)
合作探究---平行线的判定
A
B
C
D
E
F
H
G
1
2
平行线的判定方法2:
两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行。
简单说成:
内错角相等,两直线平行。
(任何一对)
∵ ∠1=∠2(已知)
∴ AB∥CD(内错角相等,两直线平行)
几何语言:
合作探究---平行线的判定
【问题2】如图,∠1+∠2=180°,求证:AB∥CD.
证明:∵ ∠1+∠2=180° (已知)
∠1+∠3=180° (邻补角定义)
∴ AB∥CD
(同角的补角相等)
∴∠3=∠2
3
2
A
B
C
D
E
F
1
(同位角相等,两直线平行)
合作探究---平行线的判定
A
B
C
D
E
F
H
G
1
2
平行线的判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行。
简单说成:
同旁内角互补,两直线平行。
(任何一对)
∵ ∠1+∠2=180°(已知)
∴ AB∥CD(内错角相等,两直线平行)
几何语言:
还有其他证明方法吗?
合作探究---平行线的判定
【问题3】在同一平面内,如果两条直线都垂直于 同一条直线,那么这两条直线平行吗?为什么?
解:这两条直线平行。理由如下:
如图,已知:直线 a⊥c,b⊥c,求证:直线 a∥b
a
b
c
1
2
证明:∵ a⊥c,b⊥c (已知)
∴∠1=∠2=90° (垂直的定义)
∴ 直线 a∥b
(同位角相等,两直线平行)
合作探究---平行线的判定
平行线的判定方法4:
在同一平面内,如果两条直线都垂直于 同一条直线,那么这两条直线平行。
∴ AB∥CD
几何语言:
a
b
c
1
2
∵ a⊥c,b⊥c (已知)
归纳总结
同位角相等,两直线平行。
判定方法1:
判定方法2:
内错角相等,两直线平行。
判定方法3:
同旁内角互补,两直线平行。
判定方法4:
平行于同一条直线的两条直线互相平行。
判定方法5:
垂直于同一条直线的两条直线互相平行。
前提条件:在同一个平面内!
综合演练
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
知识点拨:同位角相等,两直线平行。
综合演练
2.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. B. C . D.
C
知识点拨:内错角相等,两直线平行。
A
B
C
D
E
F
H
G
1
2
2
A
B
C
D
)
1
)
1
2
C
D
A
B
A
B
C
D
1
2
综合演练
3.如图,已知∠1=70 °要使AB∥CE,则需要具备的另一个条件是( )
A.∠2= 70 °B. ∠2=100 ° C. ∠2= 110 °D. ∠3= 110 °
C
知识点拨:同旁内角互补,两直线平行。
F
2
3
1
E
D
C
B
A
综合演练
① ∵ ∠1 =_____(已知)
∴ AB∥CE( )
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
4.根据条件完成填空.
综合演练
5.如图,E是AB上一点,F是DC上一点,G是BC延长线上一点。
⑴ 如果∠B=∠DCG,可以判断哪两条直线平行?
为什么?
A
B
C
D
E
F
G
解:∵∠B=∠DCG (已知)
∴ 直线AB∥CD
(同位角相等,两直线平行)
综合演练
⑵ 如果∠D=∠DCG,可以判断哪两条直线平行?
为什么?
A
B
C
D
E
F
G
解:∵∠D=∠DCG (已知)
∴ 直线AD∥BG
(内错角相等,两直线平行)
综合演练
⑶ 如果∠D+∠DFE=180°,可以判断哪两条直线平行?
为什么?
A
B
C
D
E
F
G
解:∵∠D+∠DFE=180° (已知)
∴ 直线AD∥EF
(同旁内角互补,两直线平行)
综合演练
理由如下:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
6.如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
课后作业
课本教材第15页:4、6题
https://www.21cnjy.com/help/help_extract.php
人教版 七年级数学下
5.2.2平行线的判定
学习目标
1.掌握平行线的三种判定方法,会运用判定方法来判断两条直线是否平行;(重点)
2.能够根据平行线的判定方法进行简单的推理.(难点)
回顾旧知
问题1 在同一平面内,两条不重合的直线的位置关系有哪几种?
问题2 怎样的两条直线平行?
问题3 上节课你学了平行线的哪些内容?
相交(包括垂直)和平行两种.
在同一平面内,不相交的两条直线平行.
2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
1.经过直线外一点,有且只有一条直线与已知直线平行.
回顾旧知
思考: 根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否相交来判定是否平行,那么有没有其他判定方法呢?
合作探究---平行线的判定
●
一、放
二、靠
三、移
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
合作探究---平行线的判定
b
A
2
1
a
B
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
同位角
平行
合作探究---平行线的判定
(3)将其最初和最终的两种特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(4) 由上面的操作过程,你能发现判定两直线平行的方法吗?
合作探究---平行线的判定
A
B
C
D
E
F
H
G
1
2
平行线的判定方法1:
两条直线被第三条直线所截,如果同位角相等,
那么这两条直线平行。
简单说成:
同位角相等,两直线平行。
(任何一对)
∵ ∠1=∠2(已知)
∴ AB∥CD(同位角相等,两直线平行)
几何语言:
小试牛刀
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
同位角相等,两直线平行.
合作探究---平行线的判定
3
证明:∵ ∠1=∠2 (已知)
∴ AB∥CD
2
A
B
C
D
E
F
1
【问题1】如图,已知∠1=∠2,求证:AB∥CD.
∠1=∠3 (对顶角相等)
∴∠2=∠3 (等量代换)
(同位角相等,两直线平行)
合作探究---平行线的判定
A
B
C
D
E
F
H
G
1
2
平行线的判定方法2:
两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行。
简单说成:
内错角相等,两直线平行。
(任何一对)
∵ ∠1=∠2(已知)
∴ AB∥CD(内错角相等,两直线平行)
几何语言:
合作探究---平行线的判定
【问题2】如图,∠1+∠2=180°,求证:AB∥CD.
证明:∵ ∠1+∠2=180° (已知)
∠1+∠3=180° (邻补角定义)
∴ AB∥CD
(同角的补角相等)
∴∠3=∠2
3
2
A
B
C
D
E
F
1
(同位角相等,两直线平行)
合作探究---平行线的判定
A
B
C
D
E
F
H
G
1
2
平行线的判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行。
简单说成:
同旁内角互补,两直线平行。
(任何一对)
∵ ∠1+∠2=180°(已知)
∴ AB∥CD(内错角相等,两直线平行)
几何语言:
还有其他证明方法吗?
合作探究---平行线的判定
【问题3】在同一平面内,如果两条直线都垂直于 同一条直线,那么这两条直线平行吗?为什么?
解:这两条直线平行。理由如下:
如图,已知:直线 a⊥c,b⊥c,求证:直线 a∥b
a
b
c
1
2
证明:∵ a⊥c,b⊥c (已知)
∴∠1=∠2=90° (垂直的定义)
∴ 直线 a∥b
(同位角相等,两直线平行)
合作探究---平行线的判定
平行线的判定方法4:
在同一平面内,如果两条直线都垂直于 同一条直线,那么这两条直线平行。
∴ AB∥CD
几何语言:
a
b
c
1
2
∵ a⊥c,b⊥c (已知)
归纳总结
同位角相等,两直线平行。
判定方法1:
判定方法2:
内错角相等,两直线平行。
判定方法3:
同旁内角互补,两直线平行。
判定方法4:
平行于同一条直线的两条直线互相平行。
判定方法5:
垂直于同一条直线的两条直线互相平行。
前提条件:在同一个平面内!
综合演练
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
知识点拨:同位角相等,两直线平行。
综合演练
2.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. B. C . D.
C
知识点拨:内错角相等,两直线平行。
A
B
C
D
E
F
H
G
1
2
2
A
B
C
D
)
1
)
1
2
C
D
A
B
A
B
C
D
1
2
综合演练
3.如图,已知∠1=70 °要使AB∥CE,则需要具备的另一个条件是( )
A.∠2= 70 °B. ∠2=100 ° C. ∠2= 110 °D. ∠3= 110 °
C
知识点拨:同旁内角互补,两直线平行。
F
2
3
1
E
D
C
B
A
综合演练
① ∵ ∠1 =_____(已知)
∴ AB∥CE( )
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
4.根据条件完成填空.
综合演练
5.如图,E是AB上一点,F是DC上一点,G是BC延长线上一点。
⑴ 如果∠B=∠DCG,可以判断哪两条直线平行?
为什么?
A
B
C
D
E
F
G
解:∵∠B=∠DCG (已知)
∴ 直线AB∥CD
(同位角相等,两直线平行)
综合演练
⑵ 如果∠D=∠DCG,可以判断哪两条直线平行?
为什么?
A
B
C
D
E
F
G
解:∵∠D=∠DCG (已知)
∴ 直线AD∥BG
(内错角相等,两直线平行)
综合演练
⑶ 如果∠D+∠DFE=180°,可以判断哪两条直线平行?
为什么?
A
B
C
D
E
F
G
解:∵∠D+∠DFE=180° (已知)
∴ 直线AD∥EF
(同旁内角互补,两直线平行)
综合演练
理由如下:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
6.如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
课后作业
课本教材第15页:4、6题
https://www.21cnjy.com/help/help_extract.php
