第八章 机械能守恒定律应用—单物体运动圆周运动临界问题(共23张ppt)
文档属性
| 名称 | 第八章 机械能守恒定律应用—单物体运动圆周运动临界问题(共23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 470.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-31 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
机械能守恒定律应用(一)
单物体运动
单体机械能守恒定律表达式:
二、研究物体的能量转化过程:
复习:
1、机械能:定义、注意的问题
2、机械能守恒定律:
条件:
一:研究物体的初末状态:
注意零势面
(1)确定研究对象,画出过程示意图;
应用机械能守恒定律解题的一般步骤:
(2)受力分析,做功分析,检验守恒条件;
(3)选取参考平面,确定物体初、末状态的机械能(势能和动能);
(4)根据机械能守恒定律列方程求解。
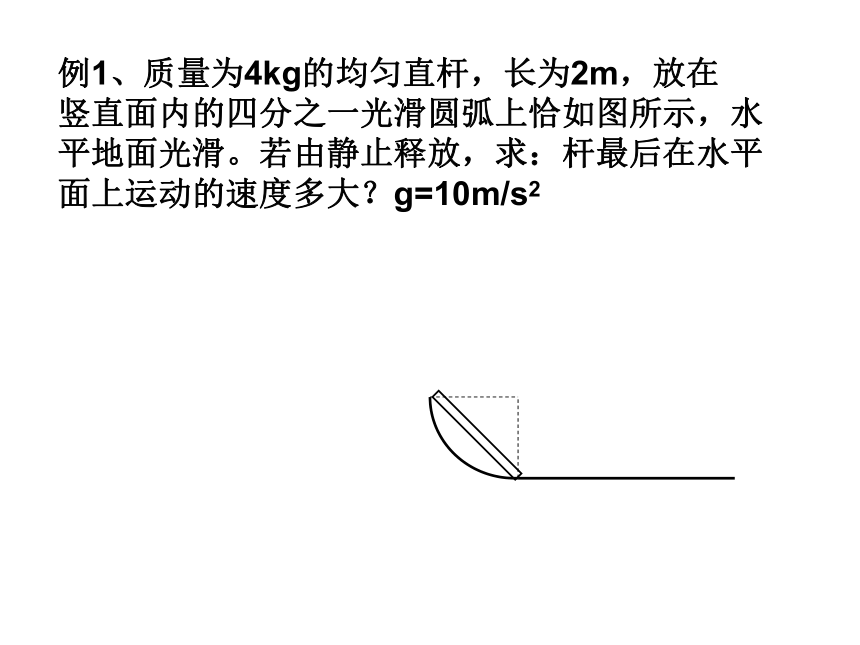
例1、质量为4kg的均匀直杆,长为2m,放在
竖直面内的四分之一光滑圆弧上恰如图所示,水
平地面光滑。若由静止释放,求:杆最后在水平
面上运动的速度多大?g=10m/s2
例2:在地面以8m/s的初速度抛出一个石块,若初速度与水平成60°。取g=10m/s2 。
求:1)石块在最高点速度多大?
石块能达到的最大高度是多少?
2)怎样抛出,能达到的高度最大?
例题3:细绳和小球连在一起,悬挂在O点。已知:
绳长L=0.2m,球质量m=0.2kg,g=10m/s2. 将绳
拉直在水平位置给小球竖直向下的初速度v0=2m/s,
则小球在竖直面内摆动。
求:1)经过最低点时,小球的速度多大?
2)在最低点时,绳的拉力多大?
解:小球摆动的过程中,机械能守恒:
以最低点为参考平面
在最低点处:
例题4:将质量5kg的物体轻放在竖直的轻弹簧上,
物体向下运动到最低点时,下落0.2m的距离。
求:此时的弹簧的弹性势能多大?g=10m/s2
小球和弹簧系统,机械能守恒:
小球的重力势能减少等于弹簧的弹性势能的增加
方法: 研究系统内能量之间的转化
若地面、小球均与弹簧相连,将弹簧拉长
10cm后由静止释放,当小球将弹簧压缩
10cm时,速度多大?
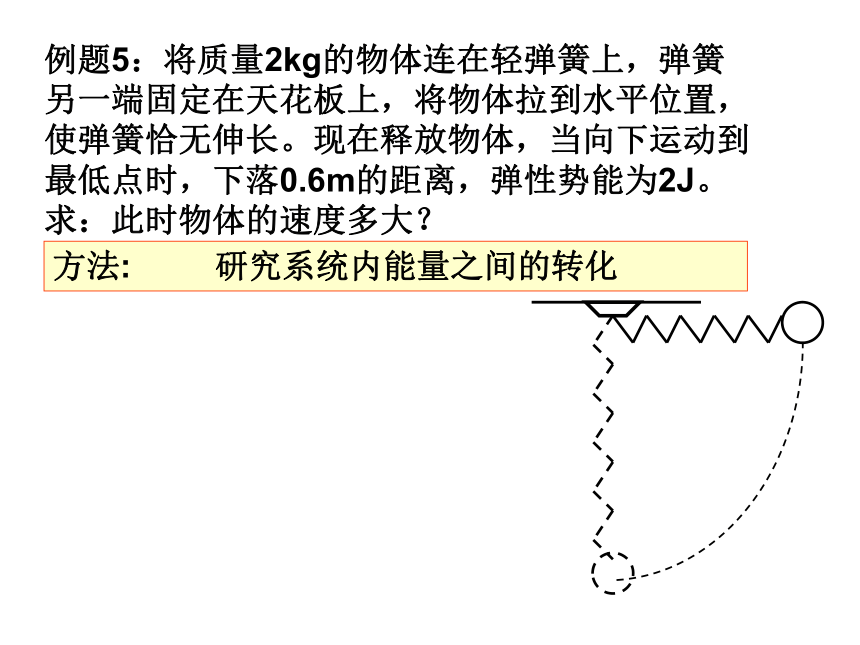
例题5:将质量2kg的物体连在轻弹簧上,弹簧
另一端固定在天花板上,将物体拉到水平位置,
使弹簧恰无伸长。现在释放物体,当向下运动到
最低点时,下落0.6m的距离,弹性势能为2J。
求:此时物体的速度多大?
方法: 研究系统内能量之间的转化
答:(1)3m/s (2)3.2N 方向向下
例6
例 7. 一根内壁光滑的细圆管,形状如下图所示,放在竖直平面内,一个小球自A口的正上方高h处自由落下,第一次小球恰能抵达B点;第二次落入A口后,自B口射出,恰能再进入A口,则两次小球下落的高度之比h1:h2= ______
解:第一次恰能抵达B点,不难看出
v B1=0
由机械能守恒定律
mg h1 =mgR+1/2·mvB12
∴h1 =R
第二次从B点平抛
R=vB2t R=1/2·gt 2
mg h2 =mgR+1/2·mvB22
h2 =5R/4
h1 :h2 = 4:5
4:5
例题、小球沿光滑斜面由静止从A点开始下滑,A高为h1=6m,B高h2=1m, 求小球到达B点时的速率。
G
N
小球从A到B过程中机械能守恒。
以斜面底面为参考平面。
A
B
机械能守恒求解:
G
G
N
A
B
机械能守恒定律:关注初末状态的机械能的关系
即 能与能的关系 ;
利用 时,会算能量变化。
例题、小球沿光滑斜面由静止开始下滑,A高为h1=6m,B高h2=1m, 求小球到达斜面底端时的速率。
小球从A到B过程,减少的重力势能等于增加的动能
机械能守恒定律应用(二)
机械能守恒+圆周运动的临界问题
例题1:如图,竖直面内的光滑轨道,底部水平半圆
部分的半径为R=2m,球质量m=2kg,g=10m/s2.
求:给小球多大的初速度,小球可以恰好通过轨道
的最高点?
10m/s
在一过程中,使用机械能守恒定律,
建立两个位置间速度关系 ;
在一个位置处,使用向心力公式,
建立力与速度的关系
例2、如图示,长为l 的轻质硬棒的底端和中点各固定一个质量为m的小球,为使轻质硬棒能绕转轴O转到最高点,则底端小球在如图示位置应具有的最小速度v= 。
解:系统的机械能守恒,
因为小球转到最高点的最小速度可以为0 ,所以,
例3:如甲图所示,小球以v0初速度沿光滑的斜面可
以上升到最大高度B处。则在a、b、c、d四个图中,
小球均以相等速度v0切入光滑的轨道,则四个图中,
小球能上升到与B等高处的是__________图。
ACD
例4:如图:
例5. 小球A用不可伸长的轻绳悬于O点,在O点的正下方有一固定的钉子B,OB=d,初始时小球A与O同水平面无初速释放,绳长为L,绳的最大承受能力为9mg。为使球能绕B点做完整的圆周运动,试求d的取值范围?
习题课
机械能守恒+极值讨论
机械能守恒+弹簧+恰要分离
例题1:如图所示,半径为r,质量不计的圆盘与地面垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点r/2处固定一个质量也为m的小球B.放开盘让其自由转动,问:
(1)A球转到最低点时的线速度是多少?
(2)在转动过程中半径OA向左偏离竖直方向的最大角度是多少?
例2;如图:两等长的杆固定连接,在O处穿过一光滑
水平固定转轴,杆两端AB物体质量为M、2M,从
图示位置由静止释放,求:转动中两球的最大速
度.杆长为L。
例题3:质量均为m的A、B物块,用轻弹簧连接在一起,
竖直放置静止,如图所示。A物体连接一轻绳,绕过定
滑轮与一个不计质量的挂钩相连,绳恰拉直。现将一
个2m的物块C挂在挂钩上,由静止释放,若弹簧劲度系
数为k,则当物块B恰要离地时,物块c的速度多大?
例4、如所示,质量为m1的物体A,经一轻质弹簧与下
方地面上的质量为m2的物体B相连,弹簧的劲度系数为
k,物体A、B都处于静止状态.一不可伸长的轻绳一端绕
过轻滑轮连接物体,另一端连接一轻挂钩.开始时各段
绳都处于伸直状态,物体A上方的一段绳沿竖直方向.现
给挂钩挂一质量为m2的物体C并从静止释放,已知它恰
好能使物体B离开地面但不继续上升.若将物体C换成另
一质量为(m1+m2)的物体D,仍从上述初始位置由静止释
放,则这次物体B刚离地时物体D的速度大小是多少?
已知重力加速度为g.
机械能守恒定律应用(一)
单物体运动
单体机械能守恒定律表达式:
二、研究物体的能量转化过程:
复习:
1、机械能:定义、注意的问题
2、机械能守恒定律:
条件:
一:研究物体的初末状态:
注意零势面
(1)确定研究对象,画出过程示意图;
应用机械能守恒定律解题的一般步骤:
(2)受力分析,做功分析,检验守恒条件;
(3)选取参考平面,确定物体初、末状态的机械能(势能和动能);
(4)根据机械能守恒定律列方程求解。
例1、质量为4kg的均匀直杆,长为2m,放在
竖直面内的四分之一光滑圆弧上恰如图所示,水
平地面光滑。若由静止释放,求:杆最后在水平
面上运动的速度多大?g=10m/s2
例2:在地面以8m/s的初速度抛出一个石块,若初速度与水平成60°。取g=10m/s2 。
求:1)石块在最高点速度多大?
石块能达到的最大高度是多少?
2)怎样抛出,能达到的高度最大?
例题3:细绳和小球连在一起,悬挂在O点。已知:
绳长L=0.2m,球质量m=0.2kg,g=10m/s2. 将绳
拉直在水平位置给小球竖直向下的初速度v0=2m/s,
则小球在竖直面内摆动。
求:1)经过最低点时,小球的速度多大?
2)在最低点时,绳的拉力多大?
解:小球摆动的过程中,机械能守恒:
以最低点为参考平面
在最低点处:
例题4:将质量5kg的物体轻放在竖直的轻弹簧上,
物体向下运动到最低点时,下落0.2m的距离。
求:此时的弹簧的弹性势能多大?g=10m/s2
小球和弹簧系统,机械能守恒:
小球的重力势能减少等于弹簧的弹性势能的增加
方法: 研究系统内能量之间的转化
若地面、小球均与弹簧相连,将弹簧拉长
10cm后由静止释放,当小球将弹簧压缩
10cm时,速度多大?
例题5:将质量2kg的物体连在轻弹簧上,弹簧
另一端固定在天花板上,将物体拉到水平位置,
使弹簧恰无伸长。现在释放物体,当向下运动到
最低点时,下落0.6m的距离,弹性势能为2J。
求:此时物体的速度多大?
方法: 研究系统内能量之间的转化
答:(1)3m/s (2)3.2N 方向向下
例6
例 7. 一根内壁光滑的细圆管,形状如下图所示,放在竖直平面内,一个小球自A口的正上方高h处自由落下,第一次小球恰能抵达B点;第二次落入A口后,自B口射出,恰能再进入A口,则两次小球下落的高度之比h1:h2= ______
解:第一次恰能抵达B点,不难看出
v B1=0
由机械能守恒定律
mg h1 =mgR+1/2·mvB12
∴h1 =R
第二次从B点平抛
R=vB2t R=1/2·gt 2
mg h2 =mgR+1/2·mvB22
h2 =5R/4
h1 :h2 = 4:5
4:5
例题、小球沿光滑斜面由静止从A点开始下滑,A高为h1=6m,B高h2=1m, 求小球到达B点时的速率。
G
N
小球从A到B过程中机械能守恒。
以斜面底面为参考平面。
A
B
机械能守恒求解:
G
G
N
A
B
机械能守恒定律:关注初末状态的机械能的关系
即 能与能的关系 ;
利用 时,会算能量变化。
例题、小球沿光滑斜面由静止开始下滑,A高为h1=6m,B高h2=1m, 求小球到达斜面底端时的速率。
小球从A到B过程,减少的重力势能等于增加的动能
机械能守恒定律应用(二)
机械能守恒+圆周运动的临界问题
例题1:如图,竖直面内的光滑轨道,底部水平半圆
部分的半径为R=2m,球质量m=2kg,g=10m/s2.
求:给小球多大的初速度,小球可以恰好通过轨道
的最高点?
10m/s
在一过程中,使用机械能守恒定律,
建立两个位置间速度关系 ;
在一个位置处,使用向心力公式,
建立力与速度的关系
例2、如图示,长为l 的轻质硬棒的底端和中点各固定一个质量为m的小球,为使轻质硬棒能绕转轴O转到最高点,则底端小球在如图示位置应具有的最小速度v= 。
解:系统的机械能守恒,
因为小球转到最高点的最小速度可以为0 ,所以,
例3:如甲图所示,小球以v0初速度沿光滑的斜面可
以上升到最大高度B处。则在a、b、c、d四个图中,
小球均以相等速度v0切入光滑的轨道,则四个图中,
小球能上升到与B等高处的是__________图。
ACD
例4:如图:
例5. 小球A用不可伸长的轻绳悬于O点,在O点的正下方有一固定的钉子B,OB=d,初始时小球A与O同水平面无初速释放,绳长为L,绳的最大承受能力为9mg。为使球能绕B点做完整的圆周运动,试求d的取值范围?
习题课
机械能守恒+极值讨论
机械能守恒+弹簧+恰要分离
例题1:如图所示,半径为r,质量不计的圆盘与地面垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点r/2处固定一个质量也为m的小球B.放开盘让其自由转动,问:
(1)A球转到最低点时的线速度是多少?
(2)在转动过程中半径OA向左偏离竖直方向的最大角度是多少?
例2;如图:两等长的杆固定连接,在O处穿过一光滑
水平固定转轴,杆两端AB物体质量为M、2M,从
图示位置由静止释放,求:转动中两球的最大速
度.杆长为L。
例题3:质量均为m的A、B物块,用轻弹簧连接在一起,
竖直放置静止,如图所示。A物体连接一轻绳,绕过定
滑轮与一个不计质量的挂钩相连,绳恰拉直。现将一
个2m的物块C挂在挂钩上,由静止释放,若弹簧劲度系
数为k,则当物块B恰要离地时,物块c的速度多大?
例4、如所示,质量为m1的物体A,经一轻质弹簧与下
方地面上的质量为m2的物体B相连,弹簧的劲度系数为
k,物体A、B都处于静止状态.一不可伸长的轻绳一端绕
过轻滑轮连接物体,另一端连接一轻挂钩.开始时各段
绳都处于伸直状态,物体A上方的一段绳沿竖直方向.现
给挂钩挂一质量为m2的物体C并从静止释放,已知它恰
好能使物体B离开地面但不继续上升.若将物体C换成另
一质量为(m1+m2)的物体D,仍从上述初始位置由静止释
放,则这次物体B刚离地时物体D的速度大小是多少?
已知重力加速度为g.
