数学必修第二册 第六章《平面向量初步》教学建议课件(共28张PPT)(共28张ppt)
文档属性
| 名称 | 数学必修第二册 第六章《平面向量初步》教学建议课件(共28张PPT)(共28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 13:06:53 | ||
图片预览








文档简介
(共28张PPT)
《平面向量》教学建议
目录
课标要求
课时安排建议
教学建议
向量高考题汇编
2
3
课标要求
《普通高中数学课程标准(2017年版)》
主题三:几何与代数中:平面向量(12课时)
旧教材内容与课时安排
2.1 向量的线性运算
2.1.1向量的概念
2.1.2向量的加法
2.1.3向量的减法
2.1.4数乘向量
2.1.5向量共线条件与轴上向量坐标运算
2.2 向量的分解与向量的坐标运算
2.2.1平面向量基本定理
2.2.2向量的正交分解与向量的直角坐标运算
2.2.3 用平面向量坐标表示向量共线条件
4
2.3 平面向量的数量积
2.3.1向量数量积的物理背景与定义
2.3.2 向量数量积的运算律
2.3.3向量数量积的坐标运算与度量公式
2.4向量的应用
2.4.1向量在几何中的应用
2.4.2向量在物理中的应用
本章小结·阅读与欣赏
向量概念的推广与应用
5
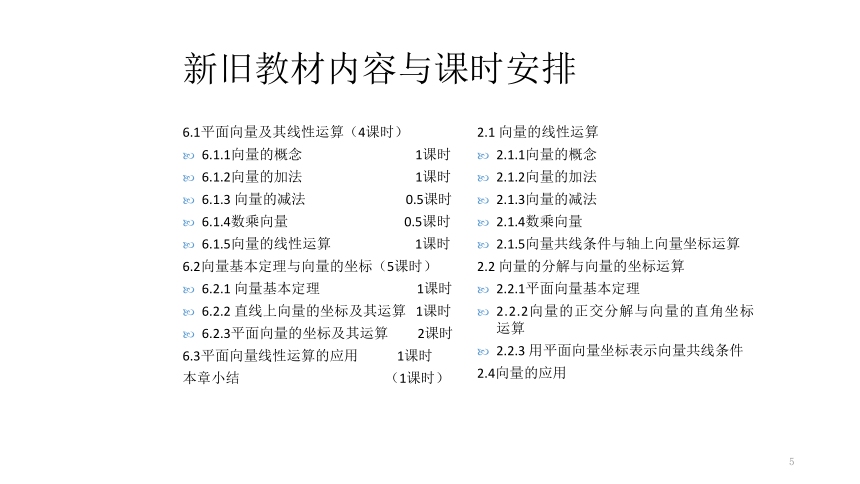
6.1平面向量及其线性运算(4课时)
6.1.1向量的概念 1课时
6.1.2向量的加法 1课时
6.1.3 向量的减法 0.5课时
6.1.4数乘向量 0.5课时
6.1.5向量的线性运算 1课时
6.2向量基本定理与向量的坐标(5课时)
6.2.1 向量基本定理 1课时
6.2.2 直线上向量的坐标及其运算 1课时
6.2.3平面向量的坐标及其运算 2课时
6.3平面向量线性运算的应用 1课时
本章小结 (1课时)
新旧教材内容与课时安排
2.1 向量的线性运算
2.1.1向量的概念
2.1.2向量的加法
2.1.3向量的减法
2.1.4数乘向量
2.1.5向量共线条件与轴上向量坐标运算
2.2 向量的分解与向量的坐标运算
2.2.1平面向量基本定理
2.2.2向量的正交分解与向量的直角坐标运算
2.2.3 用平面向量坐标表示向量共线条件
2.4向量的应用
6
A版和湘教版将本部分内容安排在三角函数学习的后面,整体内容含有数量积的内容。
B版放在三角函数的学习前面出现,无数量积的内容。主要是基础内容。
不建议再增加课时。
课时安排
教学建议---向量的概念中的情景的设置与引入
7
1、基于核心素养的教学,要特别重视情境的创设和问题的提出.核心素养是在特定情境中表现出来的知识、能力和态度,只有通过合适的情境才有利于学生感悟和形成.设计情境和提出问题的目的是启发学生思考,设计情境和提出问题的根基是数学内容的本质.
2、情境与问题是多样的、多层次的.情境可以包括:现实情境、数学情境、科学情境……情境与问题是联系在一起的,一个情境是否合适并不仅仅取决于情境本身,而在于所提出的问题是否能够揭示数学的本质.
8
教学建议---向量的概念中的情景的设置与引入
9
向量概念的教学主要突出情境设置,丰富的问题情境,比如物理中的速度加速度,还有风向风力的问题,以及尝试与发现,更多的给学生提供了一个理解平面向量概念的实质。既让向量具体化,又突出向量的代数与几何的特征,体现数形结合思想。同时又给学生提出双向认识向量的基本思路。
教学建议---向量的概念中的情景的设置与引入
10
教学建议---向量的概念中的情景的设置与引入
增加判断题
11
向量是数形结合的最好载体,因此向量教学中多结合几何图形,直观的说明运算法则,让学生动手做图,比如新教材中的练习题,尤其是第1道题,都设置了网格图,这样学生就可以动手操作,使他去体会一下向量的长度(模),体会向量的平移变换,理解向量运算的实质。
教学建议-------网格图的教学
12
阅读多版本的教材后,只有B版教材使用了网格图,网格图的使用更好的突出了向量的“形”,让学生动手作图,感受到向量的起始点,方向,平移,共线,平行关系等诸多相关的因素,便于学生接受并理解这个教学概念。
教学建议-------网格图的教学
13
向量线性运算单独成为一节,这样使学生更好的归纳和总结,对于加减数乘三个运算,明确他们之间的区别与联系,使学生更容易的类比出运算之间的关系,比如说他们的结果都是向量,也可以与实数运算类比,得到它们之间的区别与联系,更好地理解向量的线性运算。
教学建议------线性运算
14
数形结合思想的渗透
向量是体现数形结合思想的最好的知识载体,它既体现了代数的特点,又可以从几何图形的性质入手去研究,因此向量法解决问题更好地体现了数形结合的思想。
15
教学建议------数学思想方法的教学
类比的思想方法
最贴近学生的思维习惯,数学思维是可以教会的。
类比的教学是在这里用的非常多的一个方法,让学
生掌握它。
16
教学建议------数学思想方法的教学
类比的数学思想方法的体现
17
①法则的讲授:
向量的加法------向量的数乘(相等向量的求和)
------向量的减法(与反向量求和)
②实数与向量的运算类比:
探索实数运算与向量运算的共性与差异
18
类比的数学思想方法的体现
类比的数学思想方法的体现
③习题的编排:
数学组
19
从简单问题入手,大道至简。
问题设置有梯度,学生很容易的到相关的结论
为将来学习完向量的数量积,可以用来严格的证明
20
类比的数学思想方法的体现
④定理的类比:
共线向量基本定理-----平面向量基本定理
21
类比的数学思想方法的体现
⑤一维到二维的类比:
直线上的坐标(一维数轴)
平面上的坐标(二维平面)
22
类比的数学思想方法的体现
教学建议-----向量的工具性
向量理论具有深刻的数学内涵、丰富的物理背景。向量既是几何研究对象,也是代数研究对象,是沟通几何与代数的桥梁。向量理论是描述直线、曲线、平面、曲面以及高维空间数学问题的基本工具,是进一步学习和研究其他数学领域问题的基础,在解决实际问题中发挥重要作用。
平面向量线性运算的应用主要是两方面,一个是在平面几何中的应用,一个是在物理中的应用,
23
向量的工具性--向量的应用(几何)
24
在平面几何中重点要突出的是向量相等,那么以前咱们在初中说平行四边形,强调是两组对边平行,两组对边相等,一组对边平行且相等,而到了高中我们转化成了只要一组对边平行且相等,即向量相等,就能明确它是平行四边形。
因为在这个向量相等中,它既体现长度又体现方向,所以强调的是一组对边平行且相等。
25
向量的工具性-----向量的应用(物理)
26
向量的工具性-----向量的应用(物理)
在物理中我们所说的应用就是斜面上放的小木块,它的受力情况既有力的合成,也有力的分解。
向量高考题汇编
特点:以中低档题居多,考查内容主要涉及到四种运算、平行、垂直、坐标运算,平面向量基本定理。相关联知识有充要条件、函数、解析几何思想、不等式,通常涉及到的内容也比较简单。以前考查多以坐标为主,比较简单,近几年的考查以向量法、几何意义以及与其他知识相结合的小综合为主。可以发现高考题命题思路更关注向量的实质含义,能力立意。
27
28
谢 谢 !
《平面向量》教学建议
目录
课标要求
课时安排建议
教学建议
向量高考题汇编
2
3
课标要求
《普通高中数学课程标准(2017年版)》
主题三:几何与代数中:平面向量(12课时)
旧教材内容与课时安排
2.1 向量的线性运算
2.1.1向量的概念
2.1.2向量的加法
2.1.3向量的减法
2.1.4数乘向量
2.1.5向量共线条件与轴上向量坐标运算
2.2 向量的分解与向量的坐标运算
2.2.1平面向量基本定理
2.2.2向量的正交分解与向量的直角坐标运算
2.2.3 用平面向量坐标表示向量共线条件
4
2.3 平面向量的数量积
2.3.1向量数量积的物理背景与定义
2.3.2 向量数量积的运算律
2.3.3向量数量积的坐标运算与度量公式
2.4向量的应用
2.4.1向量在几何中的应用
2.4.2向量在物理中的应用
本章小结·阅读与欣赏
向量概念的推广与应用
5
6.1平面向量及其线性运算(4课时)
6.1.1向量的概念 1课时
6.1.2向量的加法 1课时
6.1.3 向量的减法 0.5课时
6.1.4数乘向量 0.5课时
6.1.5向量的线性运算 1课时
6.2向量基本定理与向量的坐标(5课时)
6.2.1 向量基本定理 1课时
6.2.2 直线上向量的坐标及其运算 1课时
6.2.3平面向量的坐标及其运算 2课时
6.3平面向量线性运算的应用 1课时
本章小结 (1课时)
新旧教材内容与课时安排
2.1 向量的线性运算
2.1.1向量的概念
2.1.2向量的加法
2.1.3向量的减法
2.1.4数乘向量
2.1.5向量共线条件与轴上向量坐标运算
2.2 向量的分解与向量的坐标运算
2.2.1平面向量基本定理
2.2.2向量的正交分解与向量的直角坐标运算
2.2.3 用平面向量坐标表示向量共线条件
2.4向量的应用
6
A版和湘教版将本部分内容安排在三角函数学习的后面,整体内容含有数量积的内容。
B版放在三角函数的学习前面出现,无数量积的内容。主要是基础内容。
不建议再增加课时。
课时安排
教学建议---向量的概念中的情景的设置与引入
7
1、基于核心素养的教学,要特别重视情境的创设和问题的提出.核心素养是在特定情境中表现出来的知识、能力和态度,只有通过合适的情境才有利于学生感悟和形成.设计情境和提出问题的目的是启发学生思考,设计情境和提出问题的根基是数学内容的本质.
2、情境与问题是多样的、多层次的.情境可以包括:现实情境、数学情境、科学情境……情境与问题是联系在一起的,一个情境是否合适并不仅仅取决于情境本身,而在于所提出的问题是否能够揭示数学的本质.
8
教学建议---向量的概念中的情景的设置与引入
9
向量概念的教学主要突出情境设置,丰富的问题情境,比如物理中的速度加速度,还有风向风力的问题,以及尝试与发现,更多的给学生提供了一个理解平面向量概念的实质。既让向量具体化,又突出向量的代数与几何的特征,体现数形结合思想。同时又给学生提出双向认识向量的基本思路。
教学建议---向量的概念中的情景的设置与引入
10
教学建议---向量的概念中的情景的设置与引入
增加判断题
11
向量是数形结合的最好载体,因此向量教学中多结合几何图形,直观的说明运算法则,让学生动手做图,比如新教材中的练习题,尤其是第1道题,都设置了网格图,这样学生就可以动手操作,使他去体会一下向量的长度(模),体会向量的平移变换,理解向量运算的实质。
教学建议-------网格图的教学
12
阅读多版本的教材后,只有B版教材使用了网格图,网格图的使用更好的突出了向量的“形”,让学生动手作图,感受到向量的起始点,方向,平移,共线,平行关系等诸多相关的因素,便于学生接受并理解这个教学概念。
教学建议-------网格图的教学
13
向量线性运算单独成为一节,这样使学生更好的归纳和总结,对于加减数乘三个运算,明确他们之间的区别与联系,使学生更容易的类比出运算之间的关系,比如说他们的结果都是向量,也可以与实数运算类比,得到它们之间的区别与联系,更好地理解向量的线性运算。
教学建议------线性运算
14
数形结合思想的渗透
向量是体现数形结合思想的最好的知识载体,它既体现了代数的特点,又可以从几何图形的性质入手去研究,因此向量法解决问题更好地体现了数形结合的思想。
15
教学建议------数学思想方法的教学
类比的思想方法
最贴近学生的思维习惯,数学思维是可以教会的。
类比的教学是在这里用的非常多的一个方法,让学
生掌握它。
16
教学建议------数学思想方法的教学
类比的数学思想方法的体现
17
①法则的讲授:
向量的加法------向量的数乘(相等向量的求和)
------向量的减法(与反向量求和)
②实数与向量的运算类比:
探索实数运算与向量运算的共性与差异
18
类比的数学思想方法的体现
类比的数学思想方法的体现
③习题的编排:
数学组
19
从简单问题入手,大道至简。
问题设置有梯度,学生很容易的到相关的结论
为将来学习完向量的数量积,可以用来严格的证明
20
类比的数学思想方法的体现
④定理的类比:
共线向量基本定理-----平面向量基本定理
21
类比的数学思想方法的体现
⑤一维到二维的类比:
直线上的坐标(一维数轴)
平面上的坐标(二维平面)
22
类比的数学思想方法的体现
教学建议-----向量的工具性
向量理论具有深刻的数学内涵、丰富的物理背景。向量既是几何研究对象,也是代数研究对象,是沟通几何与代数的桥梁。向量理论是描述直线、曲线、平面、曲面以及高维空间数学问题的基本工具,是进一步学习和研究其他数学领域问题的基础,在解决实际问题中发挥重要作用。
平面向量线性运算的应用主要是两方面,一个是在平面几何中的应用,一个是在物理中的应用,
23
向量的工具性--向量的应用(几何)
24
在平面几何中重点要突出的是向量相等,那么以前咱们在初中说平行四边形,强调是两组对边平行,两组对边相等,一组对边平行且相等,而到了高中我们转化成了只要一组对边平行且相等,即向量相等,就能明确它是平行四边形。
因为在这个向量相等中,它既体现长度又体现方向,所以强调的是一组对边平行且相等。
25
向量的工具性-----向量的应用(物理)
26
向量的工具性-----向量的应用(物理)
在物理中我们所说的应用就是斜面上放的小木块,它的受力情况既有力的合成,也有力的分解。
向量高考题汇编
特点:以中低档题居多,考查内容主要涉及到四种运算、平行、垂直、坐标运算,平面向量基本定理。相关联知识有充要条件、函数、解析几何思想、不等式,通常涉及到的内容也比较简单。以前考查多以坐标为主,比较简单,近几年的考查以向量法、几何意义以及与其他知识相结合的小综合为主。可以发现高考题命题思路更关注向量的实质含义,能力立意。
27
28
谢 谢 !
