人教版七年级数学下册6.3 实数课件(20张PPT)
文档属性
| 名称 | 人教版七年级数学下册6.3 实数课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-30 23:43:39 | ||
图片预览



文档简介
(共20张PPT)
6.3 实数
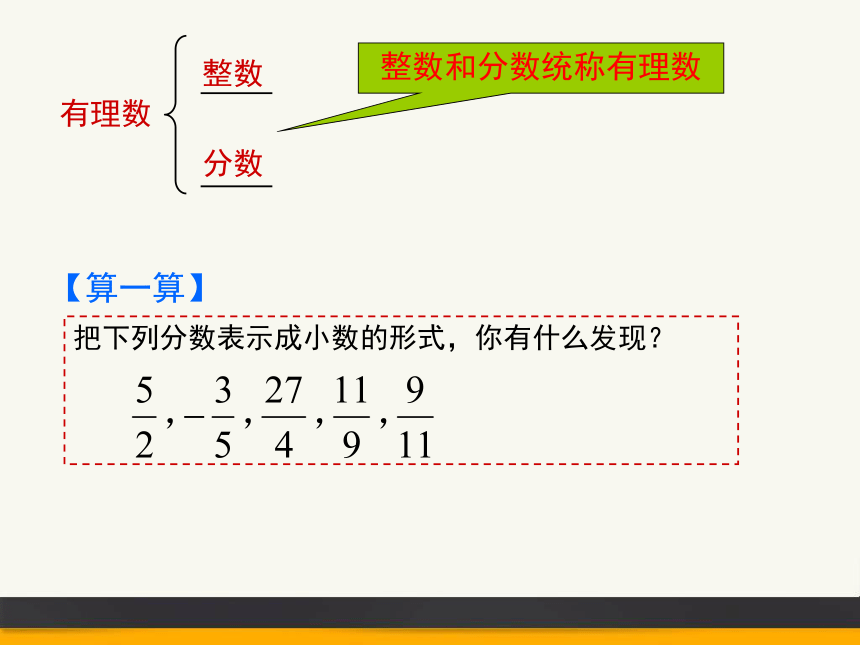
【复习】
1、到目前为止,我们已经学习了哪些数?
2、什么是有理数,有理数可以怎样分类?
3、正数的平方根怎样表示? 它有怎样的性质?
有理数
整数
分数
整数和分数统称有理数
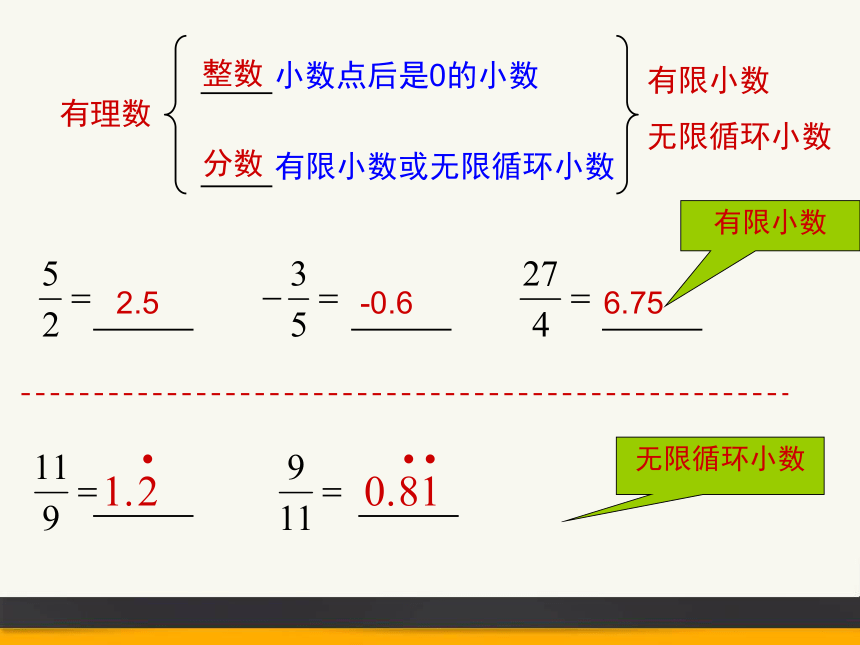
有理数
整数
分数
2.5
-0.6
6.75
有限小数
无限循环小数
有限小数或无限循环小数
小数点后是0的小数
有限小数
无限循环小数
任何一个有理数都可以写成有限小数或无限循环小数的形式
任何有限小数或无限循环小数都是有理数
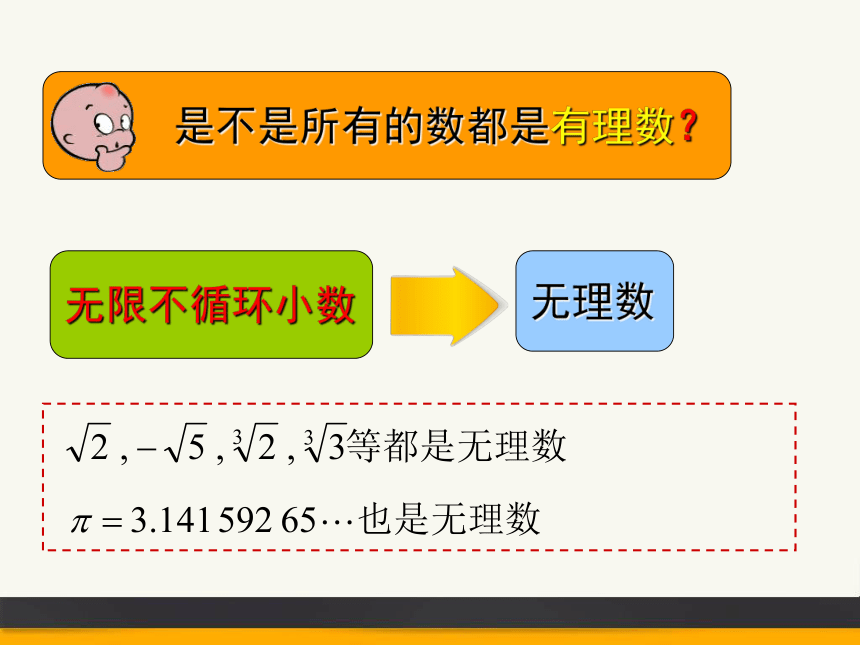
无限不循环小数
无理数
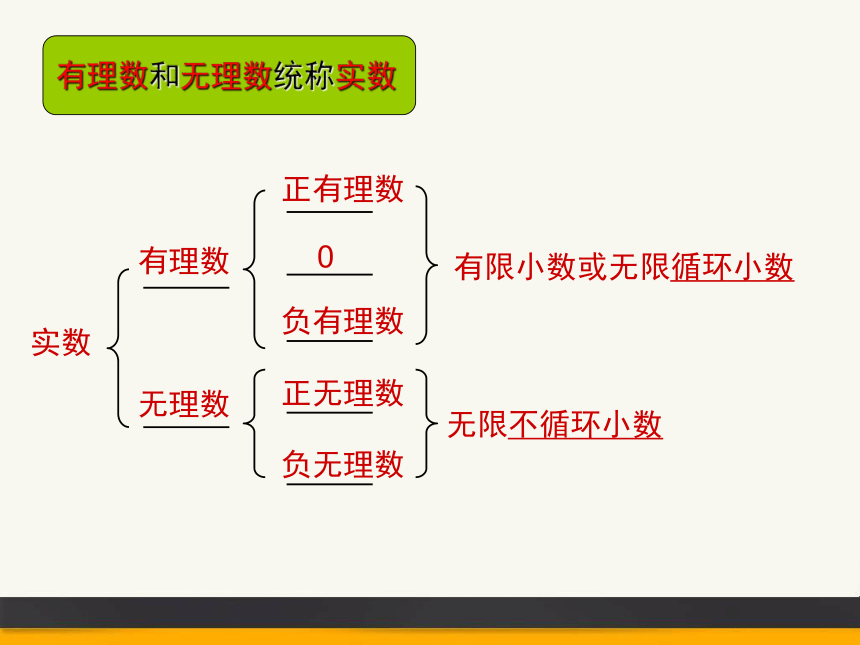
有理数和无理数统称实数
实数
有理数
无理数
正有理数
负有理数
0
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
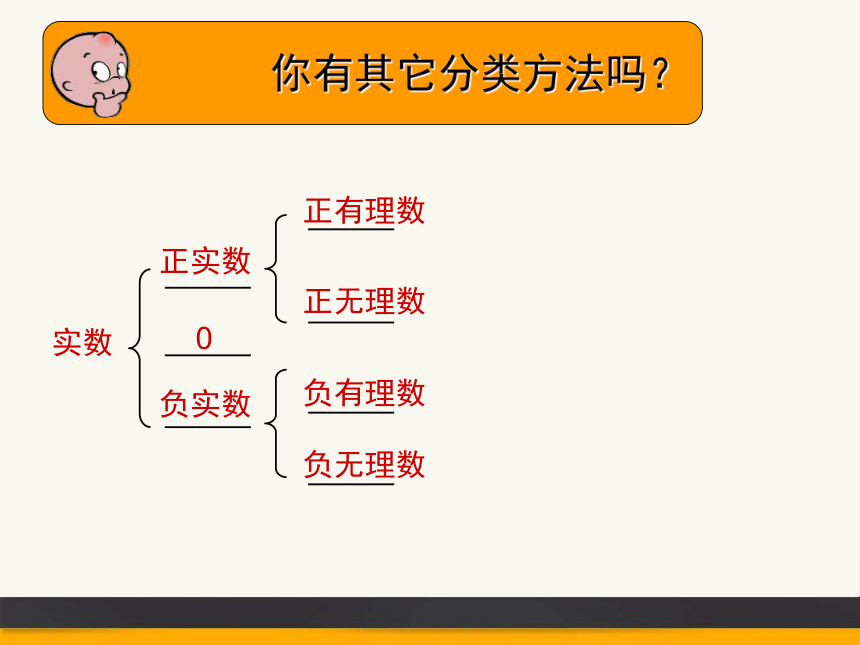
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
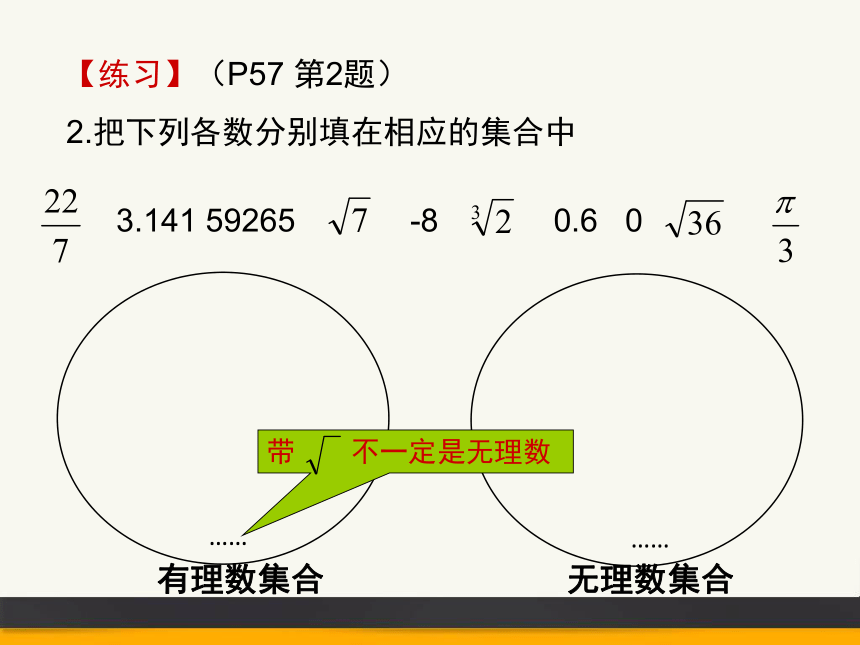
【练习】(P57 第2题)
2.把下列各数分别填在相应的集合中
……
……
有理数集合
无理数集合
3.141 59265
-8
0.6
0
【练习】
把下列各数分别填在相应的集合中
……
……
有理数集合
无理数集合
0.45
0.1010010001…
有规律不代表有循环
【想一想】
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O' ,点O' 对应的数是多少?
π
【想一想】
每一个无理数都可以用数轴上的一个点表示出来
实数与数轴上的点是一一对应的
A
0
B
C
D
4
-2
【练习】(P56 第1题)
1.将标有字母的各点与下列实数对应起来
.
.
.
.
.
E
A= B= C= .
D= E= .
-1
1
2
【练习】(P57 第1题)
1.判断下列说法是否正确
(1)无限小数都是无理数.
(2)无理数都是无限小数.
(3)带根号的数都是无理数.
(4)所有有理数都可以用数轴上的点表示,反过来,
数轴上的点都表示有理数.
(5)所有实数都可以用数轴上的点表示,反过来,
数轴上的点都表示实数.
(6)实数不是有理数就是无理数
×
√
×
×
√
√
D
■实数
有理数
无理数
有限小数或无限循环小数
无限不循环小数
■常见的无理数
①含根号且开方开不尽的数
②含π的式子
②无限不循环小数
■实数与数轴一一对应
6.3 实数
【复习】
1、到目前为止,我们已经学习了哪些数?
2、什么是有理数,有理数可以怎样分类?
3、正数的平方根怎样表示? 它有怎样的性质?
有理数
整数
分数
整数和分数统称有理数
有理数
整数
分数
2.5
-0.6
6.75
有限小数
无限循环小数
有限小数或无限循环小数
小数点后是0的小数
有限小数
无限循环小数
任何一个有理数都可以写成有限小数或无限循环小数的形式
任何有限小数或无限循环小数都是有理数
无限不循环小数
无理数
有理数和无理数统称实数
实数
有理数
无理数
正有理数
负有理数
0
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
【练习】(P57 第2题)
2.把下列各数分别填在相应的集合中
……
……
有理数集合
无理数集合
3.141 59265
-8
0.6
0
【练习】
把下列各数分别填在相应的集合中
……
……
有理数集合
无理数集合
0.45
0.1010010001…
有规律不代表有循环
【想一想】
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O' ,点O' 对应的数是多少?
π
【想一想】
每一个无理数都可以用数轴上的一个点表示出来
实数与数轴上的点是一一对应的
A
0
B
C
D
4
-2
【练习】(P56 第1题)
1.将标有字母的各点与下列实数对应起来
.
.
.
.
.
E
A= B= C= .
D= E= .
-1
1
2
【练习】(P57 第1题)
1.判断下列说法是否正确
(1)无限小数都是无理数.
(2)无理数都是无限小数.
(3)带根号的数都是无理数.
(4)所有有理数都可以用数轴上的点表示,反过来,
数轴上的点都表示有理数.
(5)所有实数都可以用数轴上的点表示,反过来,
数轴上的点都表示实数.
(6)实数不是有理数就是无理数
×
√
×
×
√
√
D
■实数
有理数
无理数
有限小数或无限循环小数
无限不循环小数
■常见的无理数
①含根号且开方开不尽的数
②含π的式子
②无限不循环小数
■实数与数轴一一对应
