人教A版 必修5 高中数学 1.2应用举例 上课课件(共39张PPT)
文档属性
| 名称 | 人教A版 必修5 高中数学 1.2应用举例 上课课件(共39张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 644.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 12:26:34 | ||
图片预览









文档简介
(共39张PPT)
新课导入
回顾旧知
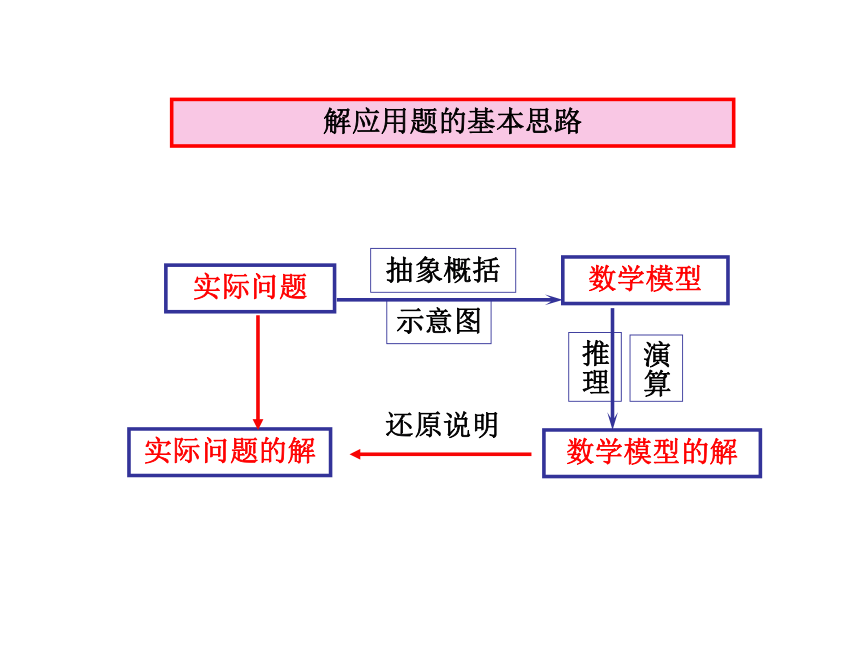
正弦定理:
R是圆的半径
余弦定理:
在生活中测量距离、高度、角度等问题上,方法很多,初中时学过应用全等三角形,相似三角形与解直角三角形等,但是有些问题不能使用这些方法了,那么使用正、余弦定理怎么样解决这些问题呢?
1.2应用举例
教学目标
知识与能力
能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题,了解常用的测量相关术语.
采用“提出问题——引发思考——探索猜想——总结规律——反馈训练”的教学过程,根据大纲要求以及教学内容之间的内在关系,铺开例题,设计变式,同时通过多媒体、图形观察等直观演示,帮助学生掌握解法,能够类比解决实际问题.
过程与方法
激发学生学习数学的兴趣,并体会数学的应用价值;同时培养学生运用图形、数学符号表达题意和应用转化思想解决数学问题的能力.
情感态度与价值观
教学重难点
由实际问题中抽象出一个或几个三角形,然后逐个解决三角形,得到实际问题的解决.
根据题意建立数学模型,画出示意图.
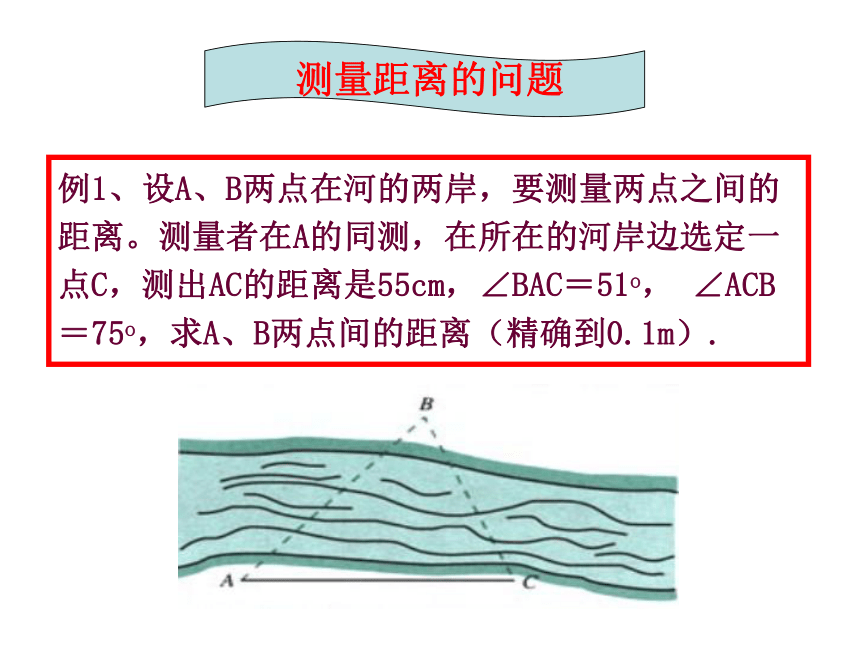
实际问题
抽象概括
示意图
数学模型
推理
演算
数学模型的解
实际问题的解
还原说明
解应用题的基本思路
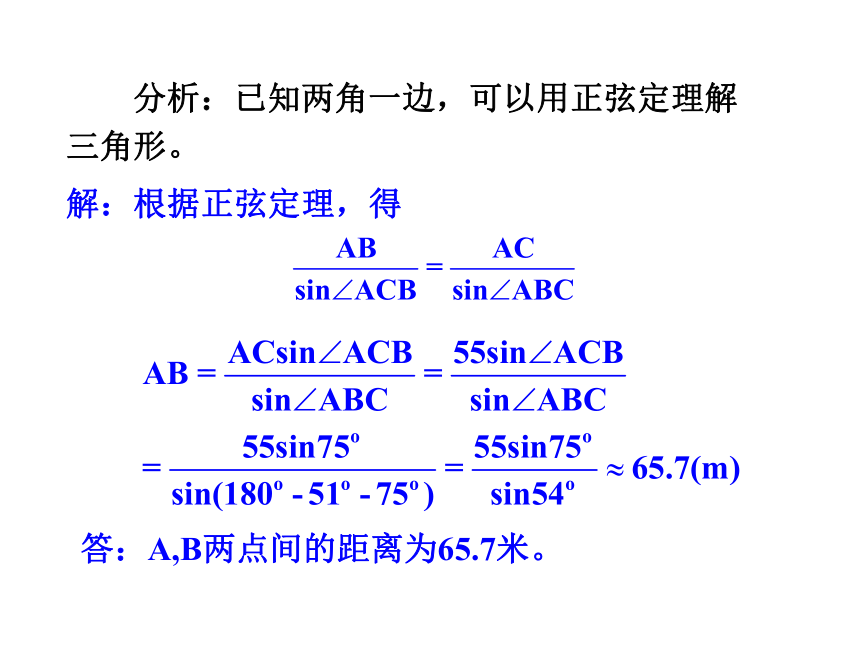
例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离是55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m).
测量距离的问题
分析:已知两角一边,可以用正弦定理解三角形。
解:根据正弦定理,得
答:A,B两点间的距离为65.7米。
例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法.
分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离.
解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在⊿ADC和⊿BDC中,应用正弦定理得
计算出AC和BC后,再在⊿ABC中,应用余弦定理计算出AB两点间的距离.
例3、 AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法.
测量高度的问题
解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在⊿ACD中,根据正弦定理可得
例4、 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m).
分析:根据已知条件,应该设法计算出AB或AC的长.
解:在⊿ABC中,∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,
CD=BD-BC≈177-27.3=150(m)
答:山的高度约为150米.
例5、 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.
解:在⊿ABC中,∠A=15°,
∠C=25°-15°=10°.
根据正弦定理,
CD=BC×tan∠DBC≈BC×tan8°≈1047(m)
答:山的高度约为1047米.
例1、在ABC中,根据下列条件,求三角形的面积S(精确到0.1cm2)
(1)已知a=14.8cm,c=23.5cm,B=148.50;
(2)已知B=62.70,C=650.8,b=3.16cm;
(3)已知三边的长分别为a=41.4cm,b=27.3cm,c=38.7cm
测量角度的问题
分析:这是一道在不同已知条件下求三角形的面积的问题,与解三角形问题有密切的关系,我们可以应用解三角形面积的知识,观察已知什么,尚缺什么?求出需要的元素,就可以求出三角形的面积。
解:(1)应用S= a c sinB,得
S= 14.8 23.5 sin148.50≈90.9(cm2)
(2)根据正弦定理,
=
c =
S = bcsinA = b2
A = 1800 - (B + C)= 1800-(62.70+ 65.80)=51.50 S ≈4.0(cm2)
(3)根据余弦定理的推论,得
cosB = = ≈0.7697
sinB = ≈ ≈0.6384
应用S= acsinB,得
S ≈511.4(cm2)
例6、在ABC中,求证:
(1)
(2)a2+b2+c2=2(bccosA+cacosB+abcosC)
分析:这是一道关于三角形边角关系恒等式的证明问题,观察式子左右两边的特点,联想到用正弦定理来证明.
证明:(1)根据正弦定理,可设
= = = k
显然 k 0,所以
左边=
= =右边
(2)根据余弦定理的推论,
右边=2(bc +ca + ab )
=(b2+c2- a2)+(c2+a2-b2)+(a2+b2-c2)
=a2+b2+c2=左边
已知在ABC中,B=30,b=6,c=6,求a及ABC的面积S.
变式练习
提示:解有关已知两边和其中一边对角的问题,注重分情况讨论解的个数 .
答案:a=6,S=9
;a=12,S=18
课堂小结
一、解斜三角形应用题的一般步骤:
(1)分析:理解题意,分清已知与未知,画出示意图.
(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型.
(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解.
(4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.
(5)评价设计.
二、利用正弦定理和余弦定理来解题时,要学会审题及根据题意画方位图,要懂得从所给的背景资料中进行加工、抽取主要因素,进行适当的简化.
三、解三角形的应用题时,通常会遇到两种情况:(1)已知量与未知量全部集中在一个三角形中,依次利用正弦定理或余弦定理解之。(2)已知量与未知量涉及两个或几个三角形,这时需要选择条件足够的三角形优先研究,再逐步在其余的三角形中求出问题的解.
四、利用正弦定理或余弦定理将已知条件转化为只含边的式子或只含角的三角函数式,然后化简并考察边或角的关系,从而确定三角形的形状。特别是有些条件既可用正弦定理也可用余弦定理甚至可以两者混用.
高考链接
1.(福建)在△ABC中,∠A,∠B,
∠C的对边分别为a,b,c,若
,则角B的值
为( )
A. B.
C. D.
D
【解析】由余弦定理知,
,∴条件等式变形为
, ,∵ ,∴B
= .
2.(山东)已知△ABC的三个角为ABC的
对边,向量 .
若 ,且acosB+BcosA=csinC,则角
B=________.
3.(全国卷)在△ABC中,内角A、B、C的
对边长分别为a、b、c.已知 ,
且 ,求b.
【解析】此题事实上比较简单,但考生反应不知从何入手.对已知条件(1) 左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2) 过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
解:由余弦定理得 ,
又 ,
又 ,
,
,
,
由正弦定理得 ,
故 。
由①② 解得,b=4.
一艘船以32.2n mile / hr的速度向正北航行。在A处看灯塔S在船的北偏东20o的方向,30min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
课堂练习
再见
新课导入
回顾旧知
正弦定理:
R是圆的半径
余弦定理:
在生活中测量距离、高度、角度等问题上,方法很多,初中时学过应用全等三角形,相似三角形与解直角三角形等,但是有些问题不能使用这些方法了,那么使用正、余弦定理怎么样解决这些问题呢?
1.2应用举例
教学目标
知识与能力
能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题,了解常用的测量相关术语.
采用“提出问题——引发思考——探索猜想——总结规律——反馈训练”的教学过程,根据大纲要求以及教学内容之间的内在关系,铺开例题,设计变式,同时通过多媒体、图形观察等直观演示,帮助学生掌握解法,能够类比解决实际问题.
过程与方法
激发学生学习数学的兴趣,并体会数学的应用价值;同时培养学生运用图形、数学符号表达题意和应用转化思想解决数学问题的能力.
情感态度与价值观
教学重难点
由实际问题中抽象出一个或几个三角形,然后逐个解决三角形,得到实际问题的解决.
根据题意建立数学模型,画出示意图.
实际问题
抽象概括
示意图
数学模型
推理
演算
数学模型的解
实际问题的解
还原说明
解应用题的基本思路
例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离是55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m).
测量距离的问题
分析:已知两角一边,可以用正弦定理解三角形。
解:根据正弦定理,得
答:A,B两点间的距离为65.7米。
例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法.
分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离.
解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在⊿ADC和⊿BDC中,应用正弦定理得
计算出AC和BC后,再在⊿ABC中,应用余弦定理计算出AB两点间的距离.
例3、 AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法.
测量高度的问题
解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在⊿ACD中,根据正弦定理可得
例4、 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m).
分析:根据已知条件,应该设法计算出AB或AC的长.
解:在⊿ABC中,∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,
CD=BD-BC≈177-27.3=150(m)
答:山的高度约为150米.
例5、 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.
解:在⊿ABC中,∠A=15°,
∠C=25°-15°=10°.
根据正弦定理,
CD=BC×tan∠DBC≈BC×tan8°≈1047(m)
答:山的高度约为1047米.
例1、在ABC中,根据下列条件,求三角形的面积S(精确到0.1cm2)
(1)已知a=14.8cm,c=23.5cm,B=148.50;
(2)已知B=62.70,C=650.8,b=3.16cm;
(3)已知三边的长分别为a=41.4cm,b=27.3cm,c=38.7cm
测量角度的问题
分析:这是一道在不同已知条件下求三角形的面积的问题,与解三角形问题有密切的关系,我们可以应用解三角形面积的知识,观察已知什么,尚缺什么?求出需要的元素,就可以求出三角形的面积。
解:(1)应用S= a c sinB,得
S= 14.8 23.5 sin148.50≈90.9(cm2)
(2)根据正弦定理,
=
c =
S = bcsinA = b2
A = 1800 - (B + C)= 1800-(62.70+ 65.80)=51.50 S ≈4.0(cm2)
(3)根据余弦定理的推论,得
cosB = = ≈0.7697
sinB = ≈ ≈0.6384
应用S= acsinB,得
S ≈511.4(cm2)
例6、在ABC中,求证:
(1)
(2)a2+b2+c2=2(bccosA+cacosB+abcosC)
分析:这是一道关于三角形边角关系恒等式的证明问题,观察式子左右两边的特点,联想到用正弦定理来证明.
证明:(1)根据正弦定理,可设
= = = k
显然 k 0,所以
左边=
= =右边
(2)根据余弦定理的推论,
右边=2(bc +ca + ab )
=(b2+c2- a2)+(c2+a2-b2)+(a2+b2-c2)
=a2+b2+c2=左边
已知在ABC中,B=30,b=6,c=6,求a及ABC的面积S.
变式练习
提示:解有关已知两边和其中一边对角的问题,注重分情况讨论解的个数 .
答案:a=6,S=9
;a=12,S=18
课堂小结
一、解斜三角形应用题的一般步骤:
(1)分析:理解题意,分清已知与未知,画出示意图.
(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型.
(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解.
(4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.
(5)评价设计.
二、利用正弦定理和余弦定理来解题时,要学会审题及根据题意画方位图,要懂得从所给的背景资料中进行加工、抽取主要因素,进行适当的简化.
三、解三角形的应用题时,通常会遇到两种情况:(1)已知量与未知量全部集中在一个三角形中,依次利用正弦定理或余弦定理解之。(2)已知量与未知量涉及两个或几个三角形,这时需要选择条件足够的三角形优先研究,再逐步在其余的三角形中求出问题的解.
四、利用正弦定理或余弦定理将已知条件转化为只含边的式子或只含角的三角函数式,然后化简并考察边或角的关系,从而确定三角形的形状。特别是有些条件既可用正弦定理也可用余弦定理甚至可以两者混用.
高考链接
1.(福建)在△ABC中,∠A,∠B,
∠C的对边分别为a,b,c,若
,则角B的值
为( )
A. B.
C. D.
D
【解析】由余弦定理知,
,∴条件等式变形为
, ,∵ ,∴B
= .
2.(山东)已知△ABC的三个角为ABC的
对边,向量 .
若 ,且acosB+BcosA=csinC,则角
B=________.
3.(全国卷)在△ABC中,内角A、B、C的
对边长分别为a、b、c.已知 ,
且 ,求b.
【解析】此题事实上比较简单,但考生反应不知从何入手.对已知条件(1) 左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2) 过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
解:由余弦定理得 ,
又 ,
又 ,
,
,
,
由正弦定理得 ,
故 。
由①② 解得,b=4.
一艘船以32.2n mile / hr的速度向正北航行。在A处看灯塔S在船的北偏东20o的方向,30min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
课堂练习
再见
