2.1数列的概念与简单表示法 课件(共47张PPT)
文档属性
| 名称 | 2.1数列的概念与简单表示法 课件(共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 882.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 13:38:01 | ||
图片预览











文档简介
(共47张PPT)
国际象棋起源于古印度,关于国际象棋还有一个传说。国王奖赏发明者,问他有什么要求,他答道:“在棋盘第一个格放1颗麦粒,在第二个格放2颗麦粒,在第三个格放4颗麦粒,在第四个格放8颗麦粒。以此类推,每个格子放的麦粒数是前一个格子的2倍,直到64个格子。国王觉得这太容易了,就欣然答应了他的要求,你认为国王能满足他的要求吗?
新课导入
4,
5,
6,
7,
8,
9,
10
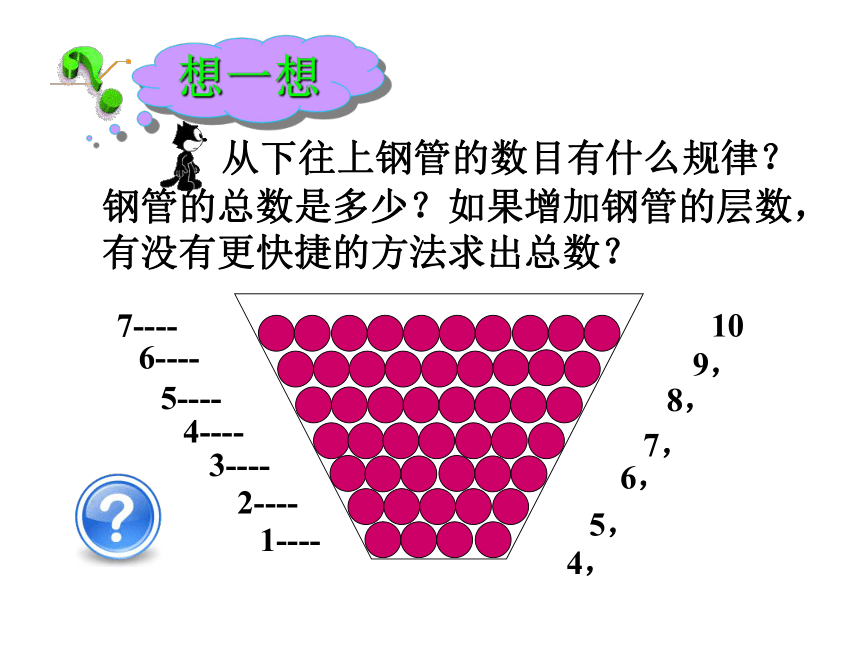
从下往上钢管的数目有什么规律?钢管的总数是多少?如果增加钢管的层数,有没有更快捷的方法求出总数?
1----
2----
3----
4----
5----
6----
7----
想一想
在本章我们将学习数列的知识,学完后解决这类问题那是小菜一碟,我们拭目以待。。。
2.1 数列的概念与简单
表示法
教学目标
(1)理解数列的概念及数列的表示方法(列表法、图象法、通项公式法),能用函数的观点认识数列;
(2)了解数列的通项公式和递推公式的意义,会根据数列的通项公式写出数列的任意一项 ;
(3)知道递推公式是给出数列的一种方法,并能根据递推公式写出数列的前n项.
知识与能力
过程与方法
(1)培养观察能力,推理能力,发展有条理地逻辑能力;
(2)经历探索数列的递推公式的的过程,体会利用递推公式获得数列每一项的过程.
情感态度与价值观
(1)经历和体验数学活动的过程以及数学在现实生活中的应用,树立学好数学的信心;
(2)让学生在民主、和谐的氛围中感受学习的乐趣;
(3)在探索求数列通项公式及其运用的过程中,培养一定的逻辑关系.
重点:数列的概念及数列的通项公式,数列递推公式的概念.
教学重难点
难点:各项的特点找出规律写出前n项的通项公式.根据递推关系求通项公式.
数列是初等数学和高等数学的一个衔接点历来是高考考察的重点,突出考察考生的思维能力、逻辑推理能力及解决问题的能力.有关数列的试题经常在数列知识、函数知识和不等式等知识网络的交汇点命题。学习中应注意应用“联系”的思想、从特殊到一般的思想方法,也要掌握常用方法.
考点分析及学法指导
请观察:
(1) 2, 3, 4, 5, 6,
(2) 1,3, 32 ,33,34,…
(3) 0, 10, 20, 30, …, 1000
(5) -1, 1, -1, 1, -1, …
(4) ….
(6) 66, 56, 34, 21, 11…
向上面的例子中,按一定次序排列的一列数叫数列.
数列中的每一个数叫做这个数列的项.各项依次叫做这个数列的第1项,第2项,······,第n项, ······
数列的一般形式可以写成 a1,a2,…,an,…
其中an是数列的第n项。简记为{an}.
数列的分类
(1)按项分类:可以分为有穷数列和无穷数列.
有穷数列:项数有限的数列
无穷数列:项数无限的数列
(2)按 的增减性分类:
递减数列:从第2项起,每一项都小于它的前一项的数列叫做递增数列.
摆动数列;如果从第2项起,有些项大于它的前一项,有些项小于它的前一项,这样的数列叫摆动数列.
常数列:如果它的每一项都相等,这个数列叫做常数列.
递增数列:从第2项起,每一项都不小于它的 前一项的数列叫做递增数列.
上述6个数列中的项与序号的关系有没有规律?如何总结这些规律?
数列中的每一个数都对应着一个序号,反过来,每个序号也都对应着一个数.如数列(1)
序号 1 2 3 4 5
项 2 3 4 5 6
←
←
←
←
←
如果已知一个数列的通项公式,那么依次用1,2,3,….代替公式中的n,就可以求出这个数列的各项.
从函数的观点看,数列可以看作是一个定义域为正整数集N*(或它的有限子集{1,2,…,n})的函数自变量从小到大一次取值时对应的一列函数值,且数列的通项公式也就是相应函数的解析式.
数列可以用图像来表示:(见下页)
注意:图像上这些点都是孤立的!
an
O
n
1 2 3 4 5 6 7
10
9
8
7
6
5
4
3
2
1
数列图象
是一些点
an=n+1的图象
如果数列{ an }中的第n项an与n之间的关系可以用一个公式来表示,则称此公式为数列的通项公式.
也满足
时,
才是数列的通项公式.
注意:只有当
a1
注意:
有些数列的通项公式并不唯一,如数列(5)
并不是所有的数列都有通项公式,如数列(6)
数列通项公式an=2n-1(n ≤ 64),只要依次用n=1,2,3,4,… 64代替公式中的n,就可以求出各项,也就是说,
a1=1, a2=2=2a1
a3 =4=2a2 ……
a64=263=2a63
即:a1=1, an=2an-1(2≤n ≤64)
递推公式
向上面那样,如果已知数列{an}的第一项(或前几项),且任一项 an与它的前一项an-1(或前几项)间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的递推公式.
递推公式也是给出数列的一种方法.
题型1
根据数列的前几项写出数列的一个通项公式
解决本类问题关键是观察归纳各项与对应的项数之间的联系.同时.要善于利用我们熟知的一些基本数列,建立合理的联想,转化而达到问题的解决.
例1
观察下面数列的特点,用适当的数填空,并写出每个数列的一个通项公式:
(1) (),
(2)1,2,4,8,(),32
答案
(1)括号内填 ,通项公式为:an=
(2)括号内填 16 ,通项公式为:an=2n-1
分析
(1)根据观察:分母的最小公倍数为12,把各项都改成以12为分母的分数.
(2)一看都是2的倍数,则要分析是2的几次幂.
例2
(1) 3,8,15,24,…
-1, 3, -6, 10, …
1, 0, 0, 0,…
6,66,666,6666,…
写出下面数列的通项公式,是它们的前四项分别是下列各数:
例2解析:
(1) 注意观察各项与对应序号的关系,可以发现:
3=1×3, 8=2×4, 15=3×5, 24=4×6
所以an=n(n+2)。
本小题也可以与数列4,9,16, 25,…(n+1)2比较,得出:
an=(n+2)2-1=n(n+2).
(2)各项的公共特点是负正相间。观察各项绝对值与对应序号关系,初看找不到规律,可将各项绝对值试迟疑序号:
= 1 =
=
= 2 =
=
所以:
=
于是an=(-1)n ●
数列分子是1,0重复变化,可看成是数列1,-1,1,-1…对应项和的 组成的新数列,分母是自然数列的各项,故所给数列的通项公式是
(3)所给数列可改写为 …
an =
(4) 将题设数列与数列9,99,999,9999,99999, …… an=10n-1
总结评述
已知一个数列的前几项,写出这个数列的一个通项公式时,将这个数列向我们熟悉的数列划归,是一种重要的思路.
相比较,可得an= (10n-1)
常见数列的通项公式:
(1)-1,1,-1,1,-1,1…,an= (-1)n
(2)1,2,3,4,5, … ,an= n
(3) 2 ,4,6,8,10 …,an= 2n
(4)1 ,3,5,7,9 …,an= 2n-1
(5)1,4,9,16,25 …,an= n2
(6) 9,99,999,9999 …,an= 10n-1
此题型大致分两类。一类是根据前几项的特点归纳猜想出的表达式。然后用数学归纳法证明:另一类是将已知递推关系式,用代数的一些变形技巧整理变形。然后采用累加法、累乘法、迭代法、换元法、或转化基本数列(等差或差比)方法求算通项.
题型2
已知数列的递推关系求数列的通项
例3
已知数列{an}满足下列条件,写出它的前5项,并归纳出数列的一个通项公式。
a1=0,an+1=an+(2n-1)
解:
∵
a1=0,an+1=an+(2n-1)
∴
a2=a1+(2×1-1)=1
a3=a2+(2×2-1)=4
a4=a3+(2×3-1)=9
a5=a4+(2×4-1)=16
∴
数列{an}为:0,1,4,9,16,…
∴
an=(n-1)2
例4
已知数列{an}满足a1=2,a2=5,a4=23,且an+1=Xan+Y,求实数X、Y的值.
分析:
通过地推公式求出a2,a4,解方程组,即求出未知数X、Y.
解:
由已知可得
a2=Xa1+Y 即:5=2X+Y
a3=Xa2+Y=5X+Y
a4=Xa3+Y=X(5X+Y)+Y 即:23=5a2+Xa+Y
①
②
联立① 、②得方程组
2X+Y=5
5a2+Xa+Y=23
解之得:
X=2
Y=1
或
X= -3
Y=11
1、数列的概念
数列是按照一定次序构成的一列数,其中数列中数的有序性是数列的灵魂.
2、数列的通项公式
并非每一个数列都可以写出通项公式;有些数列的通项公式也并非是唯一的.
课堂小结
如果数列{ an }中的第n项an与n之间的关系可以用一个公式来表示,则称此公式为数列的通项公式.
3、数列的分类
按项分类:
有穷数列:项数有限
无穷数列:项数无限
按 的增减性分类:
递增数列:
递减数列:
摆动数列:
常数数列:
如何求数列{an}的通项公式an的最大值?
﹖
探索延拓创新一
◆
思路一
思路二
数列是一个特殊的函数,我们可以利用函数求最值的方法去求解数列中的最值问题.
利用数列的单调性求解.
判断数列的单调性往往只需要比较相邻两项an和an+1的大小。这一点源于函数的单调性而有充分利用了数列的特殊性.
思路三
利用an最大的一个必要条件
首先求得满足条件的n的取值范围,然后找出此范围内的正整数的值,最后比较它们对应项的大小,其中最大的一项就是an的最大值.
an≥an-1
an≥an+1
求解.
◆
﹖
数列的通项公式an与前n项和公式sn
探索延拓创新二
an =
S1 , n=1
Sn-Sn-1 , n ≥ 2
an 与前n项和Sn之间的关系式为:
值得注意的是,
由前n项和sn求通项公式an=f(n)时,要n=1与n ≥ 2两种情况分别进行运算,然后验证两种情况可否用统一式子表示。若不能,就用分段函数表示.
探索延拓创新三
斐波那契数列指的是这样一个数列:
1、1、2、3、5、8、13、21、……
“斐波那契数列”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1240年,籍贯大概是比萨).
有趣的是:这样一个完全是自然数的数列,通项公式居然是用无理数来表达的.
这个数列从第三项开始,每一项都等于前两项之和.它的通项公式为:(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}(又叫“比内公式”,是用无理数表示有理数的一个范例.)(√5表示根号5)
随堂练习
一、根据下面各数列的前几项,写出数列的一个通项公式:
(1) 3,5,9,17,33,…;
(2) …
(3) …
(4) 0.9,0.99,0.999,0.9 999,…;
(5) 3,5,3,5,3,5,….
(1) 解法1 联系数列2,4,8,16,32,…, (想到这一点是关键)
(3)注意到分母分别是1×3,3×5,5×7,7×9,9×11,…为两个连续奇数的积.
(2)这个数列的各项由三部分组成:符号、分子、分母,所以应逐个考查其规律,先看符号,第一项有点违反规律,需写为 ,从而联系数列 ,再看分母,考虑数列 最后看分子,显然每个分子比分母都小3.
(4)原数列可转化成
…
(5)
,还可表示为
3,n为奇数
5,n为偶数
1. 已知数列的通项公式为an=(-1)n+1·(2n-3) ,则
a3+a4+a5=__________.
2. 已知数列的通项为an=2n(n+1),则a2+a8=_____________.
156
5
二、填空题:
国际象棋起源于古印度,关于国际象棋还有一个传说。国王奖赏发明者,问他有什么要求,他答道:“在棋盘第一个格放1颗麦粒,在第二个格放2颗麦粒,在第三个格放4颗麦粒,在第四个格放8颗麦粒。以此类推,每个格子放的麦粒数是前一个格子的2倍,直到64个格子。国王觉得这太容易了,就欣然答应了他的要求,你认为国王能满足他的要求吗?
新课导入
4,
5,
6,
7,
8,
9,
10
从下往上钢管的数目有什么规律?钢管的总数是多少?如果增加钢管的层数,有没有更快捷的方法求出总数?
1----
2----
3----
4----
5----
6----
7----
想一想
在本章我们将学习数列的知识,学完后解决这类问题那是小菜一碟,我们拭目以待。。。
2.1 数列的概念与简单
表示法
教学目标
(1)理解数列的概念及数列的表示方法(列表法、图象法、通项公式法),能用函数的观点认识数列;
(2)了解数列的通项公式和递推公式的意义,会根据数列的通项公式写出数列的任意一项 ;
(3)知道递推公式是给出数列的一种方法,并能根据递推公式写出数列的前n项.
知识与能力
过程与方法
(1)培养观察能力,推理能力,发展有条理地逻辑能力;
(2)经历探索数列的递推公式的的过程,体会利用递推公式获得数列每一项的过程.
情感态度与价值观
(1)经历和体验数学活动的过程以及数学在现实生活中的应用,树立学好数学的信心;
(2)让学生在民主、和谐的氛围中感受学习的乐趣;
(3)在探索求数列通项公式及其运用的过程中,培养一定的逻辑关系.
重点:数列的概念及数列的通项公式,数列递推公式的概念.
教学重难点
难点:各项的特点找出规律写出前n项的通项公式.根据递推关系求通项公式.
数列是初等数学和高等数学的一个衔接点历来是高考考察的重点,突出考察考生的思维能力、逻辑推理能力及解决问题的能力.有关数列的试题经常在数列知识、函数知识和不等式等知识网络的交汇点命题。学习中应注意应用“联系”的思想、从特殊到一般的思想方法,也要掌握常用方法.
考点分析及学法指导
请观察:
(1) 2, 3, 4, 5, 6,
(2) 1,3, 32 ,33,34,…
(3) 0, 10, 20, 30, …, 1000
(5) -1, 1, -1, 1, -1, …
(4) ….
(6) 66, 56, 34, 21, 11…
向上面的例子中,按一定次序排列的一列数叫数列.
数列中的每一个数叫做这个数列的项.各项依次叫做这个数列的第1项,第2项,······,第n项, ······
数列的一般形式可以写成 a1,a2,…,an,…
其中an是数列的第n项。简记为{an}.
数列的分类
(1)按项分类:可以分为有穷数列和无穷数列.
有穷数列:项数有限的数列
无穷数列:项数无限的数列
(2)按 的增减性分类:
递减数列:从第2项起,每一项都小于它的前一项的数列叫做递增数列.
摆动数列;如果从第2项起,有些项大于它的前一项,有些项小于它的前一项,这样的数列叫摆动数列.
常数列:如果它的每一项都相等,这个数列叫做常数列.
递增数列:从第2项起,每一项都不小于它的 前一项的数列叫做递增数列.
上述6个数列中的项与序号的关系有没有规律?如何总结这些规律?
数列中的每一个数都对应着一个序号,反过来,每个序号也都对应着一个数.如数列(1)
序号 1 2 3 4 5
项 2 3 4 5 6
←
←
←
←
←
如果已知一个数列的通项公式,那么依次用1,2,3,….代替公式中的n,就可以求出这个数列的各项.
从函数的观点看,数列可以看作是一个定义域为正整数集N*(或它的有限子集{1,2,…,n})的函数自变量从小到大一次取值时对应的一列函数值,且数列的通项公式也就是相应函数的解析式.
数列可以用图像来表示:(见下页)
注意:图像上这些点都是孤立的!
an
O
n
1 2 3 4 5 6 7
10
9
8
7
6
5
4
3
2
1
数列图象
是一些点
an=n+1的图象
如果数列{ an }中的第n项an与n之间的关系可以用一个公式来表示,则称此公式为数列的通项公式.
也满足
时,
才是数列的通项公式.
注意:只有当
a1
注意:
有些数列的通项公式并不唯一,如数列(5)
并不是所有的数列都有通项公式,如数列(6)
数列通项公式an=2n-1(n ≤ 64),只要依次用n=1,2,3,4,… 64代替公式中的n,就可以求出各项,也就是说,
a1=1, a2=2=2a1
a3 =4=2a2 ……
a64=263=2a63
即:a1=1, an=2an-1(2≤n ≤64)
递推公式
向上面那样,如果已知数列{an}的第一项(或前几项),且任一项 an与它的前一项an-1(或前几项)间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的递推公式.
递推公式也是给出数列的一种方法.
题型1
根据数列的前几项写出数列的一个通项公式
解决本类问题关键是观察归纳各项与对应的项数之间的联系.同时.要善于利用我们熟知的一些基本数列,建立合理的联想,转化而达到问题的解决.
例1
观察下面数列的特点,用适当的数填空,并写出每个数列的一个通项公式:
(1) (),
(2)1,2,4,8,(),32
答案
(1)括号内填 ,通项公式为:an=
(2)括号内填 16 ,通项公式为:an=2n-1
分析
(1)根据观察:分母的最小公倍数为12,把各项都改成以12为分母的分数.
(2)一看都是2的倍数,则要分析是2的几次幂.
例2
(1) 3,8,15,24,…
-1, 3, -6, 10, …
1, 0, 0, 0,…
6,66,666,6666,…
写出下面数列的通项公式,是它们的前四项分别是下列各数:
例2解析:
(1) 注意观察各项与对应序号的关系,可以发现:
3=1×3, 8=2×4, 15=3×5, 24=4×6
所以an=n(n+2)。
本小题也可以与数列4,9,16, 25,…(n+1)2比较,得出:
an=(n+2)2-1=n(n+2).
(2)各项的公共特点是负正相间。观察各项绝对值与对应序号关系,初看找不到规律,可将各项绝对值试迟疑序号:
= 1 =
=
= 2 =
=
所以:
=
于是an=(-1)n ●
数列分子是1,0重复变化,可看成是数列1,-1,1,-1…对应项和的 组成的新数列,分母是自然数列的各项,故所给数列的通项公式是
(3)所给数列可改写为 …
an =
(4) 将题设数列与数列9,99,999,9999,99999, …… an=10n-1
总结评述
已知一个数列的前几项,写出这个数列的一个通项公式时,将这个数列向我们熟悉的数列划归,是一种重要的思路.
相比较,可得an= (10n-1)
常见数列的通项公式:
(1)-1,1,-1,1,-1,1…,an= (-1)n
(2)1,2,3,4,5, … ,an= n
(3) 2 ,4,6,8,10 …,an= 2n
(4)1 ,3,5,7,9 …,an= 2n-1
(5)1,4,9,16,25 …,an= n2
(6) 9,99,999,9999 …,an= 10n-1
此题型大致分两类。一类是根据前几项的特点归纳猜想出的表达式。然后用数学归纳法证明:另一类是将已知递推关系式,用代数的一些变形技巧整理变形。然后采用累加法、累乘法、迭代法、换元法、或转化基本数列(等差或差比)方法求算通项.
题型2
已知数列的递推关系求数列的通项
例3
已知数列{an}满足下列条件,写出它的前5项,并归纳出数列的一个通项公式。
a1=0,an+1=an+(2n-1)
解:
∵
a1=0,an+1=an+(2n-1)
∴
a2=a1+(2×1-1)=1
a3=a2+(2×2-1)=4
a4=a3+(2×3-1)=9
a5=a4+(2×4-1)=16
∴
数列{an}为:0,1,4,9,16,…
∴
an=(n-1)2
例4
已知数列{an}满足a1=2,a2=5,a4=23,且an+1=Xan+Y,求实数X、Y的值.
分析:
通过地推公式求出a2,a4,解方程组,即求出未知数X、Y.
解:
由已知可得
a2=Xa1+Y 即:5=2X+Y
a3=Xa2+Y=5X+Y
a4=Xa3+Y=X(5X+Y)+Y 即:23=5a2+Xa+Y
①
②
联立① 、②得方程组
2X+Y=5
5a2+Xa+Y=23
解之得:
X=2
Y=1
或
X= -3
Y=11
1、数列的概念
数列是按照一定次序构成的一列数,其中数列中数的有序性是数列的灵魂.
2、数列的通项公式
并非每一个数列都可以写出通项公式;有些数列的通项公式也并非是唯一的.
课堂小结
如果数列{ an }中的第n项an与n之间的关系可以用一个公式来表示,则称此公式为数列的通项公式.
3、数列的分类
按项分类:
有穷数列:项数有限
无穷数列:项数无限
按 的增减性分类:
递增数列:
递减数列:
摆动数列:
常数数列:
如何求数列{an}的通项公式an的最大值?
﹖
探索延拓创新一
◆
思路一
思路二
数列是一个特殊的函数,我们可以利用函数求最值的方法去求解数列中的最值问题.
利用数列的单调性求解.
判断数列的单调性往往只需要比较相邻两项an和an+1的大小。这一点源于函数的单调性而有充分利用了数列的特殊性.
思路三
利用an最大的一个必要条件
首先求得满足条件的n的取值范围,然后找出此范围内的正整数的值,最后比较它们对应项的大小,其中最大的一项就是an的最大值.
an≥an-1
an≥an+1
求解.
◆
﹖
数列的通项公式an与前n项和公式sn
探索延拓创新二
an =
S1 , n=1
Sn-Sn-1 , n ≥ 2
an 与前n项和Sn之间的关系式为:
值得注意的是,
由前n项和sn求通项公式an=f(n)时,要n=1与n ≥ 2两种情况分别进行运算,然后验证两种情况可否用统一式子表示。若不能,就用分段函数表示.
探索延拓创新三
斐波那契数列指的是这样一个数列:
1、1、2、3、5、8、13、21、……
“斐波那契数列”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1240年,籍贯大概是比萨).
有趣的是:这样一个完全是自然数的数列,通项公式居然是用无理数来表达的.
这个数列从第三项开始,每一项都等于前两项之和.它的通项公式为:(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}(又叫“比内公式”,是用无理数表示有理数的一个范例.)(√5表示根号5)
随堂练习
一、根据下面各数列的前几项,写出数列的一个通项公式:
(1) 3,5,9,17,33,…;
(2) …
(3) …
(4) 0.9,0.99,0.999,0.9 999,…;
(5) 3,5,3,5,3,5,….
(1) 解法1 联系数列2,4,8,16,32,…, (想到这一点是关键)
(3)注意到分母分别是1×3,3×5,5×7,7×9,9×11,…为两个连续奇数的积.
(2)这个数列的各项由三部分组成:符号、分子、分母,所以应逐个考查其规律,先看符号,第一项有点违反规律,需写为 ,从而联系数列 ,再看分母,考虑数列 最后看分子,显然每个分子比分母都小3.
(4)原数列可转化成
…
(5)
,还可表示为
3,n为奇数
5,n为偶数
1. 已知数列的通项公式为an=(-1)n+1·(2n-3) ,则
a3+a4+a5=__________.
2. 已知数列的通项为an=2n(n+1),则a2+a8=_____________.
156
5
二、填空题:
