高中数学 必修四 1.3三角函数的诱导公式 上课课件(共39张PPT)
文档属性
| 名称 | 高中数学 必修四 1.3三角函数的诱导公式 上课课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 00:00:00 | ||
图片预览









文档简介
(共39张PPT)
问题1:
能否把 任意角的三角函数求值,化为我们熟悉的0°~360°间的角的三角函数求值问题呢?
诱导公式 一:
新课导入
能否再把0°~360°间的角的三角函数求值,化为我们熟悉的0°~90°间的角的三角函数求值问题呢?
如果能的话,那么任意角的三角函数求值,都可以化归为锐角三角函数求值,并通过求锐角三角函数方法而得到最终解决,本课就来讨论这一问题。
问题2:
1.3 三角函数的诱导公式
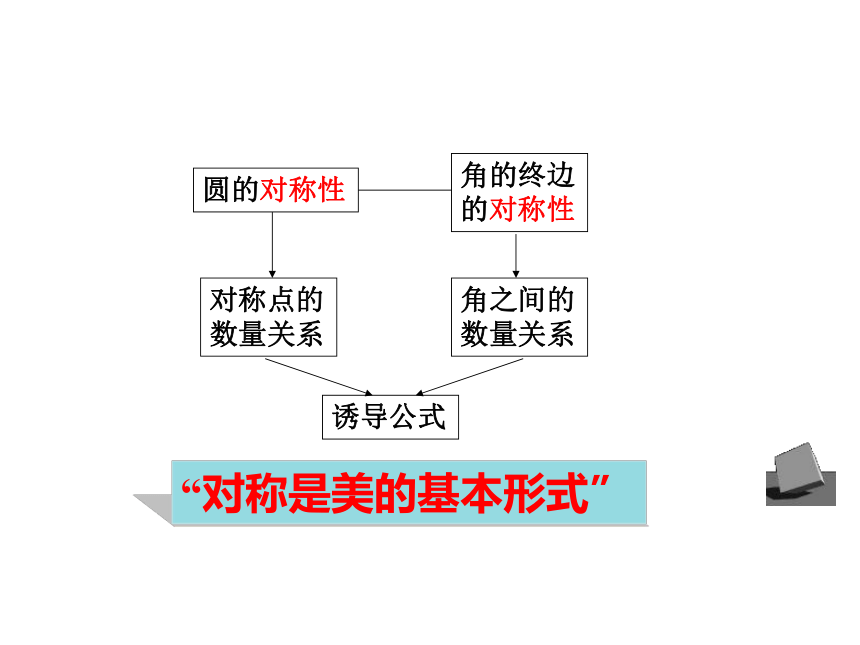
圆的对称性
角的终边的对称性
对称点的数量关系
角之间的数量关系
诱导公式
“对称是美的基本形式”
1、识记诱导公式;
2、理解和掌握公式的内涵及结构特征,会初步运用诱导公式求三角函数的值,并进行简单三角函数式的化简和证明。
学习目标
知识与能力
1、通过诱导公式的推导,培养学生的观察力、分析归纳能力,领会数学的归纳转化思想方法;
2、通过诱导公式的推导、分析公式的结构特征,使学生体验和理解从特殊到一般的数学归纳推理思维方式;
3、通过基础训练题组和能力训练题组的练习,提高学生分析问题和解决问题的实践能力。
过程与方法
1、通过诱导公式的推导,培养学生主动探索、勇于发现的科学精神,培养学生的创新意识和创新精神;
2、通过归纳思维的训练,培养学生踏实细致、严谨科学的学习习惯,渗透从特殊到一般、把未知转化为已知的辨证唯物主义思想。
情感态度与价值观
诱导公式的推导及应用。
相关角边的几何对称关系及诱导公式结构特征的认识。
学习重难点
重点:
难点:
设 0°≤α≤90°,对于任意一个 0°到360°的角β,以下四种情形中有且仅有一种成立。
问题3:
形如180°+α的三角函数值与α的三角函数值之间的关系.
单位圆:以原点为圆心,等于单位长的线段为半径作一个圆。
已知任意角α的终边与这个圆相交于点p(x,y),由于角 180°+α 的终边就是角α的终边的反向延长线,角180°+α的终边与单位圆的交于点p'(-x,-y),又因单位圆的半径 r=1,由正弦函数和余弦函数的定义得到:
1
-1
1
-1
p(x,y)
p'(-x,-y)
x
o
知识1
从而得到公式二:
1
-1
1
-1
α
-α
x
p(x,y)
p'(x,-y)
M
O
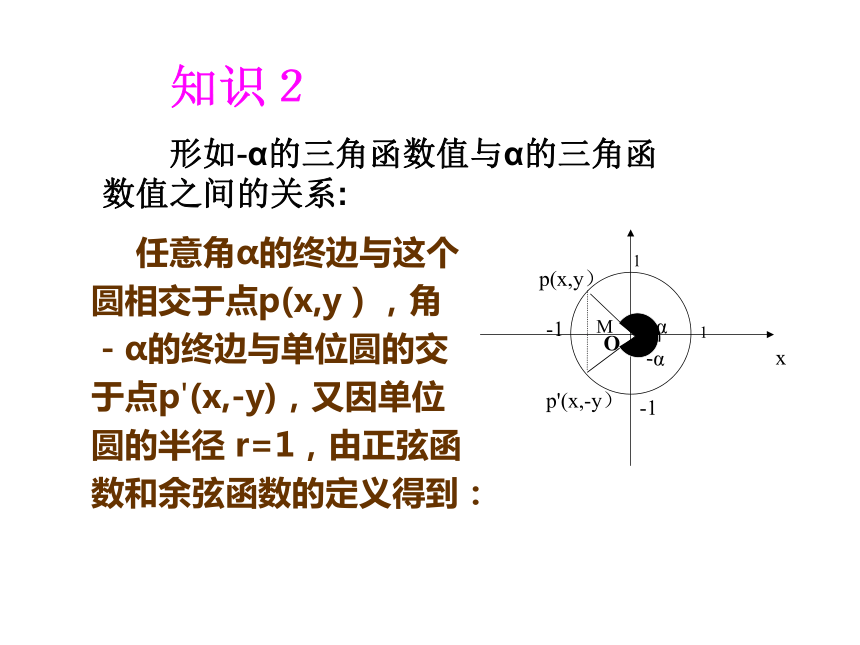
形如-α的三角函数值与α的三角函数值之间的关系:
任意角α的终边与这个圆相交于点p(x,y),角-α的终边与单位圆的交于点p'(x,-y),又因单位圆的半径 r=1,由正弦函数和余弦函数的定义得到:
知识2
从而得到公式三:
同理可得公式四:
诱导公式 一:
函数名不变,符号看象限
(将α看成锐角)。
诱导公式 二:
诱导公式 四:
函数名不变,符号看象限
(将α看成锐角)。
诱导公式 三:
我们可以用下面一段话来概括公式一~四: , , 的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
公式一、二、三、四都叫做诱导公式.
简化成“函数名不变,符号看象限”的口诀。
诱导公式小结
例1:将下列各三角函数化成锐角三角函数。
(1) sin(-699? ) (2) cos(-1525? )
(3) tan(-872? )
答案:(1) –sin21? (2) cos85?
(3) tan28?
解:⑴
⑵
⑶
例2:求三角函数值。
⑴ ⑵ ⑶
例3:已知 如何求
y
)
,
(
y
x
-
o
160
3
p
a
y
=
=
=
o
o
20
sin
380
sin
a
y
-
=
-
=
o
200
sin
a
y
-
=
-
=
-
)
20
sin(
o
a
y
=
=
o
160
sin
,
20
sin
a
=
o
o
o
o
o
160 ?
sin
),
20
sin(
,
200
sin
,
380
sin
-
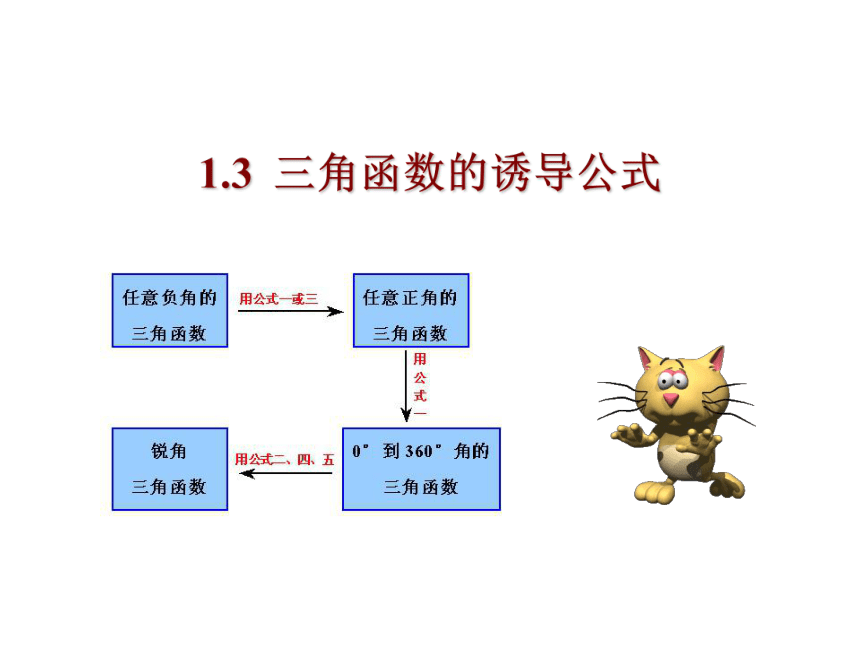
利用诱导公式把任意角的三角函数转化为锐角三角函数,一般按下面步骤进行:
任意负角的
三角函数
任意正角的
三角函数
锐角三
角函数
到 的角
的三角函数
用公式三或一
用公式一
用公式
二或四
例4:求三角函数值.
⑴ ⑵ ⑶
解:
x
o
1
-1
1
-1
任意角α的终边与单位圆相交于点 ,角 的终边与单位圆的交于点 ,又因单位圆由正弦函数和余弦函数的定义得到:
知识3
从而得公式五:
同样可得公式六:
诱导公式五:
诱导公式六:
函数名变余,符号看象限
(将α看成锐角)
综上:奇变偶不变,符号看象限.
求sinθ,cosθ,tanθ时,把θ化成θ=k· +α,则
k为奇数时,函数名变为其余函数,k为偶数时函数名不变;
符号由将α看成锐角时,θ所在象限的原来函数决定。
口诀:奇变偶不变,符号看象限.
意义:
诱导公式小结
已知 求 .
例5:
解:
2
1
20
cos
70
sin
a
-
=
=
o
o
2
1
20
cos
)
20
90
sin(
110
sin
a
-
=
=
+
=
o
o
o
o
利用公式求下列各三角函数值.
(1) (2)
例6:
解:
(1)
(2)
解:
∵
∴
∵
∴
课堂小结
我们可以用下面一段话来概括公式一~四: , , 的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
公式一、二、三、四都叫做诱导公式.
简化成“函数名不变,符号看象限”的口诀。
公式五、公式六概括如下:
简化成“奇变偶不变,符号看象限”的口诀。
1、函数式
化简的结果是( )
B.±(sin2-cos2)
C. cos2-sin2
D.以上结论都不对
A.sin2-cos2
A
课堂练习
2、填空:
(2)
答案:(1)0; (2)0.
(1)tan675°+tan765°-tan(-330°)+tan(-690°)____________.
3、化简
解:
∵
又∵
∴
答案:(1)
(2)
4、化简
(2)
(1)
问题1:
能否把 任意角的三角函数求值,化为我们熟悉的0°~360°间的角的三角函数求值问题呢?
诱导公式 一:
新课导入
能否再把0°~360°间的角的三角函数求值,化为我们熟悉的0°~90°间的角的三角函数求值问题呢?
如果能的话,那么任意角的三角函数求值,都可以化归为锐角三角函数求值,并通过求锐角三角函数方法而得到最终解决,本课就来讨论这一问题。
问题2:
1.3 三角函数的诱导公式
圆的对称性
角的终边的对称性
对称点的数量关系
角之间的数量关系
诱导公式
“对称是美的基本形式”
1、识记诱导公式;
2、理解和掌握公式的内涵及结构特征,会初步运用诱导公式求三角函数的值,并进行简单三角函数式的化简和证明。
学习目标
知识与能力
1、通过诱导公式的推导,培养学生的观察力、分析归纳能力,领会数学的归纳转化思想方法;
2、通过诱导公式的推导、分析公式的结构特征,使学生体验和理解从特殊到一般的数学归纳推理思维方式;
3、通过基础训练题组和能力训练题组的练习,提高学生分析问题和解决问题的实践能力。
过程与方法
1、通过诱导公式的推导,培养学生主动探索、勇于发现的科学精神,培养学生的创新意识和创新精神;
2、通过归纳思维的训练,培养学生踏实细致、严谨科学的学习习惯,渗透从特殊到一般、把未知转化为已知的辨证唯物主义思想。
情感态度与价值观
诱导公式的推导及应用。
相关角边的几何对称关系及诱导公式结构特征的认识。
学习重难点
重点:
难点:
设 0°≤α≤90°,对于任意一个 0°到360°的角β,以下四种情形中有且仅有一种成立。
问题3:
形如180°+α的三角函数值与α的三角函数值之间的关系.
单位圆:以原点为圆心,等于单位长的线段为半径作一个圆。
已知任意角α的终边与这个圆相交于点p(x,y),由于角 180°+α 的终边就是角α的终边的反向延长线,角180°+α的终边与单位圆的交于点p'(-x,-y),又因单位圆的半径 r=1,由正弦函数和余弦函数的定义得到:
1
-1
1
-1
p(x,y)
p'(-x,-y)
x
o
知识1
从而得到公式二:
1
-1
1
-1
α
-α
x
p(x,y)
p'(x,-y)
M
O
形如-α的三角函数值与α的三角函数值之间的关系:
任意角α的终边与这个圆相交于点p(x,y),角-α的终边与单位圆的交于点p'(x,-y),又因单位圆的半径 r=1,由正弦函数和余弦函数的定义得到:
知识2
从而得到公式三:
同理可得公式四:
诱导公式 一:
函数名不变,符号看象限
(将α看成锐角)。
诱导公式 二:
诱导公式 四:
函数名不变,符号看象限
(将α看成锐角)。
诱导公式 三:
我们可以用下面一段话来概括公式一~四: , , 的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
公式一、二、三、四都叫做诱导公式.
简化成“函数名不变,符号看象限”的口诀。
诱导公式小结
例1:将下列各三角函数化成锐角三角函数。
(1) sin(-699? ) (2) cos(-1525? )
(3) tan(-872? )
答案:(1) –sin21? (2) cos85?
(3) tan28?
解:⑴
⑵
⑶
例2:求三角函数值。
⑴ ⑵ ⑶
例3:已知 如何求
y
)
,
(
y
x
-
o
160
3
p
a
y
=
=
=
o
o
20
sin
380
sin
a
y
-
=
-
=
o
200
sin
a
y
-
=
-
=
-
)
20
sin(
o
a
y
=
=
o
160
sin
,
20
sin
a
=
o
o
o
o
o
160 ?
sin
),
20
sin(
,
200
sin
,
380
sin
-
利用诱导公式把任意角的三角函数转化为锐角三角函数,一般按下面步骤进行:
任意负角的
三角函数
任意正角的
三角函数
锐角三
角函数
到 的角
的三角函数
用公式三或一
用公式一
用公式
二或四
例4:求三角函数值.
⑴ ⑵ ⑶
解:
x
o
1
-1
1
-1
任意角α的终边与单位圆相交于点 ,角 的终边与单位圆的交于点 ,又因单位圆由正弦函数和余弦函数的定义得到:
知识3
从而得公式五:
同样可得公式六:
诱导公式五:
诱导公式六:
函数名变余,符号看象限
(将α看成锐角)
综上:奇变偶不变,符号看象限.
求sinθ,cosθ,tanθ时,把θ化成θ=k· +α,则
k为奇数时,函数名变为其余函数,k为偶数时函数名不变;
符号由将α看成锐角时,θ所在象限的原来函数决定。
口诀:奇变偶不变,符号看象限.
意义:
诱导公式小结
已知 求 .
例5:
解:
2
1
20
cos
70
sin
a
-
=
=
o
o
2
1
20
cos
)
20
90
sin(
110
sin
a
-
=
=
+
=
o
o
o
o
利用公式求下列各三角函数值.
(1) (2)
例6:
解:
(1)
(2)
解:
∵
∴
∵
∴
课堂小结
我们可以用下面一段话来概括公式一~四: , , 的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
公式一、二、三、四都叫做诱导公式.
简化成“函数名不变,符号看象限”的口诀。
公式五、公式六概括如下:
简化成“奇变偶不变,符号看象限”的口诀。
1、函数式
化简的结果是( )
B.±(sin2-cos2)
C. cos2-sin2
D.以上结论都不对
A.sin2-cos2
A
课堂练习
2、填空:
(2)
答案:(1)0; (2)0.
(1)tan675°+tan765°-tan(-330°)+tan(-690°)____________.
3、化简
解:
∵
又∵
∴
答案:(1)
(2)
4、化简
(2)
(1)
