1.6三角函数模型的简单应用 课件(共32张PPT)
文档属性
| 名称 | 1.6三角函数模型的简单应用 课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
现实生活中,如果某种变化着的现象具有周期性,那么它就可以借助三角函数来描述。
新课导入
1.6三角函数模型的简单应用
学生能够从实际问题中发现周期性变化的规律,把发现的规律抽象为恰当的三角模型,并解决相关的实际问题。
学习目标
知识与能力
让学生体验一些具有周期性变化规律的实际问题的数学“建模”思想,从而培养学生的创新精神和实践能力。
过程与方法
让学生切身感受数学建模的过程,体验数学在解决实际问题中的价值和作用。
情感态度与价值观
用三角函数模型解决一些具有周期性变化规律的实际问题。
学习重难点
重点:
从实际问题中抽取基本的数学关系来建立数学模型,并调动相关学科的知识来解决问题。
难点:
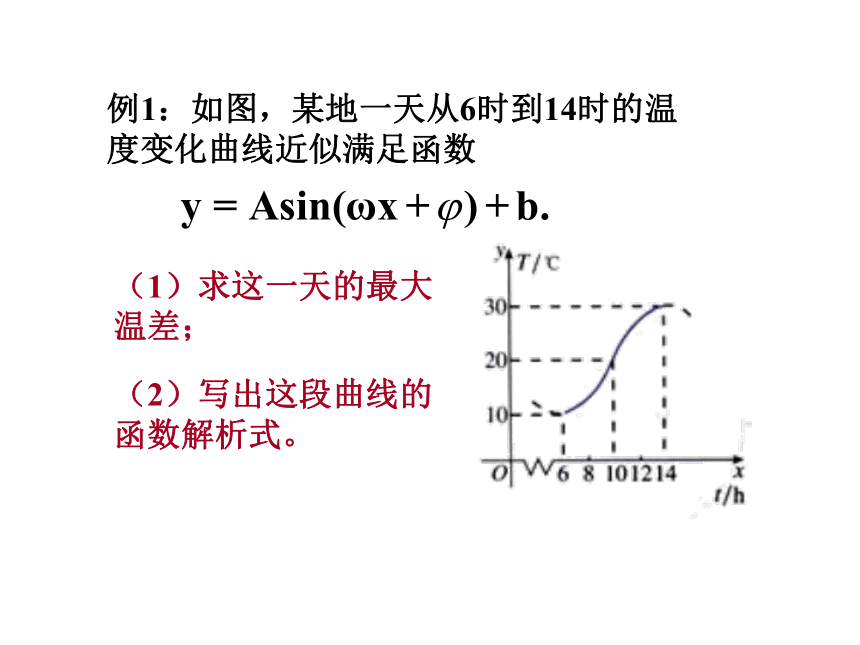
例1:如图,某地一天从6时到14时的温度变化曲线近似满足函数
(2)写出这段曲线的函数解析式。
(1)求这一天的最大温差;
解:
(1)观察图象可知,这段时间的最大温差是20?C。
(2)从图中可以看出,从6时到14时的图象是函数y=Asin(ωx+φ) +b的半个周期的图象,所以
因为点(6,10)是五点法作图中的第四点,故
故,所求函数解析式为
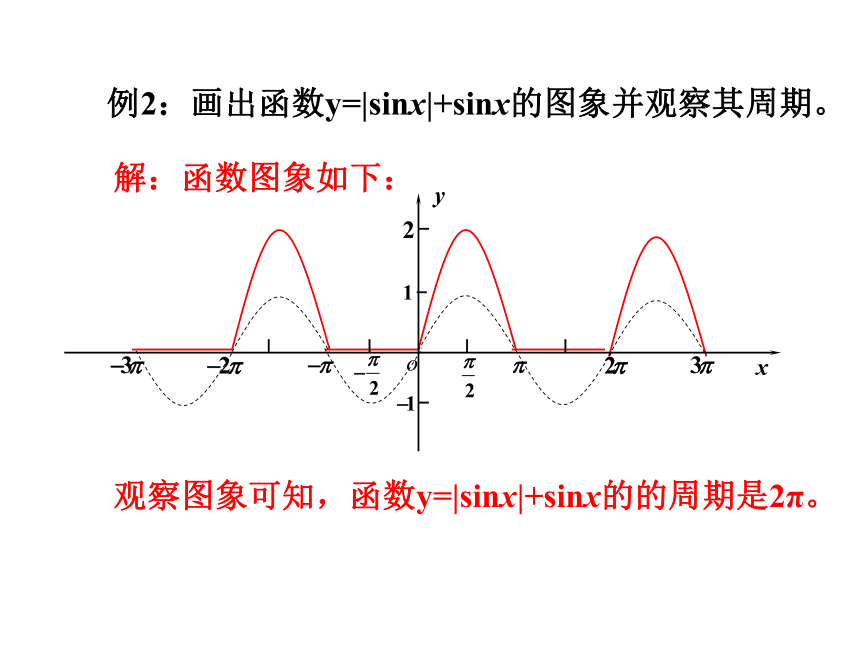
例2:画出函数y=|sinx|+sinx的图象并观察其周期。
解:函数图象如下:
观察图象可知,函数y=|sinx|+sinx的的周期是2π。
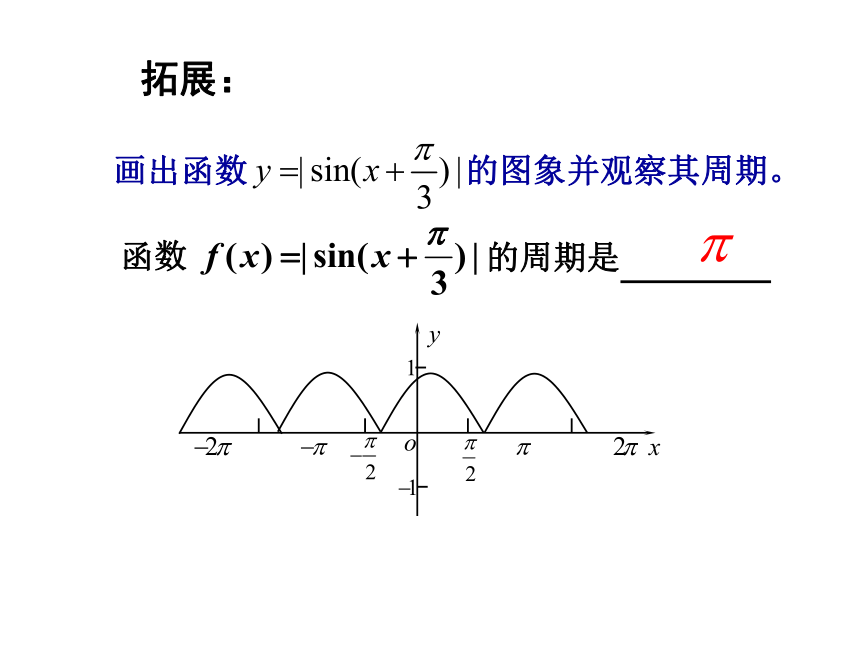
拓展:
画出函数 的图象并观察其周期。
函数
的周期是
例3:如图,设地球表面某地正午太阳高度角为θ,δ为此时太阳直射纬度, 为该地的纬度值,那么这三个量之间的关系是θ=90?-| - δ |。当地夏半年δ取正值,冬半年δ取负值。
如果在北京地区(纬度数约为北纬40?)的一幢高为H的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?
太阳光
H
解:如图,A、B、C分别太阳直射北回归线、赤道、南回归线时,楼顶在地面上的投影点,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线的情况考虑,此时的太阳直射纬度为-3?26‘,依题意两楼的间距应不小于MC。
根据太阳高度角的定义,有∠C=90?-|40?-(-23?26')|=26?34'
所以,
即在盖楼时,为使后楼不被前楼遮挡,要留出相当于楼高两倍的间距。
例4:海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋,下面是某港口在某季节每天的时间与水深的关系表:
时刻 水深(米) 时刻 水深(米) 时刻 水深(米)
0:00 5.0 9:00 2.5 18:00 5.0
3:00 7.5 12:00 5.0 21:00 2.5
6:00 5.0 15:00 7.5 24:00 5.0
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,并给出整点时的水深的近似数值(精确到0.001)。
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),该船何时能进入港口?在港口能呆多久?
(3)若某船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
(1)以时间为横坐标,水深为纵坐标,在直角坐标系中画出散点图,根据图象,可以考虑用函数
A=2.5,h=5,T=12, =0;
由 ,得
解:
来刻画水深与时间之间的对应关系.从数据和图象可以得出:
所以,这个港口的水深与时间的关系可以近似描述为:
由上述关系式易得港口在整点时水深的近似值:
时刻 0:00 1:00 2:00 3:00 4:00 5:00 6:00 7:00 8:00 9:00 10:00 11:00
水深 5.000 6.250 7.165 7.5 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754
时刻 12:00 13:00 14:00 15:00 14:00 17:00 18:00 19:00 20:00 21:00 22:00 23:00
水深 5.000 6.250 7.165 7.5 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754
(2)货船需要的安全水深为 4+1.5=5.5 (米),所以当y≥5.5时就可以进港.
令
由计算器计算可得
解得
解:
化简得
因为 ,所以有函数周期性易得
因此,货船可以在凌晨零时30分左右进港,早晨5时30分左右出港;或在中午12时30分左右进港,下午17时30分左右出港,每次可以在港口停留5小时左右。
解:
(3)设在时刻x船舶的安全水深为y,那么y=5.5-0.3(x-2) (x≥2),在同一坐标系内作出这两个函数的图象,可以看
到在6时到7时之间两个函数图象有一个交点。
通过计算可得在6时的水深约为5米,此时船舶的安全水深约为4.3米;6.5时的水深约为4.2米,此时船舶的安全水深约为4.1米;7时的水深约为3.8米,而船舶的安全水深约为4米,因此为了安全,船舶最好在6.5时之前停止卸货,将船舶驶向较深的水域。
三角函数应用模型的三种模式:一是给定呈周期变化规律的三角函数模型,根据所给模型,结合三角函数的性质,解决一些实际问题;二是给定呈周期变化的图象,利用待定系数法求出函数模型,再解决其他问题;三是搜集一个实际问题的调查数据,根据数据作出散点图,通过拟合函数图象,求出可以近似表示变化规律的函数模型,进一步用函数模型来解决问题。
课堂小结
现实问题
现实模型
改造
三角函数模型
抽象 概括
解析式
图形
三角函数模型的解
数学 方法
还原 说明
现实模型的解
是否符合实际 修改
1、一台发电机产生的交流电的电压V和时间t之间关系的图象如下图所示,则电压V和时间t之间的函数解析式为 .
V=536sin100πt,t∈[0,+∞)
课堂练习
2、如右上图,单摆从某点开始来回摆动,离开平衡位置O的距离s cm和时间t s的函数关系式为s=6sin(2πt+ ),那么单摆来回摆动一次所需的时间为( )
A.2π s
C.0.5s
B.πs
D.1s
D
3、已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位:时)的函数,记做
下表是某日各时的浪高数据:
t 0 3 6 9 12 15 18 21 24
y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,
的曲线可近似地看成是函数
(2)依据规定,当海浪高度不低于1米时才对冲浪爱好者开放,请根据(1)的结论,判断一天内的上午8:00至18:00时这段时间内,有______个小时可供冲浪爱好者进行运动。
6
(1)根据以上数据,写出函数
的函数表达式____________。
4、如图,摩天轮的半径为50m,圆心O点距地面的高度为60m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处,已知在时刻t(min)时点P距离地面的高度
(II)求证:不论t为何值时
为定值。
(I)求在2006min时点P距离地面的高度;
解:(I)由题意可知:
即
又
得
即点P距离地面的高度为85m。
(II)由(I)知
故不论t为何值,都是定值。
现实生活中,如果某种变化着的现象具有周期性,那么它就可以借助三角函数来描述。
新课导入
1.6三角函数模型的简单应用
学生能够从实际问题中发现周期性变化的规律,把发现的规律抽象为恰当的三角模型,并解决相关的实际问题。
学习目标
知识与能力
让学生体验一些具有周期性变化规律的实际问题的数学“建模”思想,从而培养学生的创新精神和实践能力。
过程与方法
让学生切身感受数学建模的过程,体验数学在解决实际问题中的价值和作用。
情感态度与价值观
用三角函数模型解决一些具有周期性变化规律的实际问题。
学习重难点
重点:
从实际问题中抽取基本的数学关系来建立数学模型,并调动相关学科的知识来解决问题。
难点:
例1:如图,某地一天从6时到14时的温度变化曲线近似满足函数
(2)写出这段曲线的函数解析式。
(1)求这一天的最大温差;
解:
(1)观察图象可知,这段时间的最大温差是20?C。
(2)从图中可以看出,从6时到14时的图象是函数y=Asin(ωx+φ) +b的半个周期的图象,所以
因为点(6,10)是五点法作图中的第四点,故
故,所求函数解析式为
例2:画出函数y=|sinx|+sinx的图象并观察其周期。
解:函数图象如下:
观察图象可知,函数y=|sinx|+sinx的的周期是2π。
拓展:
画出函数 的图象并观察其周期。
函数
的周期是
例3:如图,设地球表面某地正午太阳高度角为θ,δ为此时太阳直射纬度, 为该地的纬度值,那么这三个量之间的关系是θ=90?-| - δ |。当地夏半年δ取正值,冬半年δ取负值。
如果在北京地区(纬度数约为北纬40?)的一幢高为H的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?
太阳光
H
解:如图,A、B、C分别太阳直射北回归线、赤道、南回归线时,楼顶在地面上的投影点,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线的情况考虑,此时的太阳直射纬度为-3?26‘,依题意两楼的间距应不小于MC。
根据太阳高度角的定义,有∠C=90?-|40?-(-23?26')|=26?34'
所以,
即在盖楼时,为使后楼不被前楼遮挡,要留出相当于楼高两倍的间距。
例4:海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋,下面是某港口在某季节每天的时间与水深的关系表:
时刻 水深(米) 时刻 水深(米) 时刻 水深(米)
0:00 5.0 9:00 2.5 18:00 5.0
3:00 7.5 12:00 5.0 21:00 2.5
6:00 5.0 15:00 7.5 24:00 5.0
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,并给出整点时的水深的近似数值(精确到0.001)。
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),该船何时能进入港口?在港口能呆多久?
(3)若某船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
(1)以时间为横坐标,水深为纵坐标,在直角坐标系中画出散点图,根据图象,可以考虑用函数
A=2.5,h=5,T=12, =0;
由 ,得
解:
来刻画水深与时间之间的对应关系.从数据和图象可以得出:
所以,这个港口的水深与时间的关系可以近似描述为:
由上述关系式易得港口在整点时水深的近似值:
时刻 0:00 1:00 2:00 3:00 4:00 5:00 6:00 7:00 8:00 9:00 10:00 11:00
水深 5.000 6.250 7.165 7.5 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754
时刻 12:00 13:00 14:00 15:00 14:00 17:00 18:00 19:00 20:00 21:00 22:00 23:00
水深 5.000 6.250 7.165 7.5 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754
(2)货船需要的安全水深为 4+1.5=5.5 (米),所以当y≥5.5时就可以进港.
令
由计算器计算可得
解得
解:
化简得
因为 ,所以有函数周期性易得
因此,货船可以在凌晨零时30分左右进港,早晨5时30分左右出港;或在中午12时30分左右进港,下午17时30分左右出港,每次可以在港口停留5小时左右。
解:
(3)设在时刻x船舶的安全水深为y,那么y=5.5-0.3(x-2) (x≥2),在同一坐标系内作出这两个函数的图象,可以看
到在6时到7时之间两个函数图象有一个交点。
通过计算可得在6时的水深约为5米,此时船舶的安全水深约为4.3米;6.5时的水深约为4.2米,此时船舶的安全水深约为4.1米;7时的水深约为3.8米,而船舶的安全水深约为4米,因此为了安全,船舶最好在6.5时之前停止卸货,将船舶驶向较深的水域。
三角函数应用模型的三种模式:一是给定呈周期变化规律的三角函数模型,根据所给模型,结合三角函数的性质,解决一些实际问题;二是给定呈周期变化的图象,利用待定系数法求出函数模型,再解决其他问题;三是搜集一个实际问题的调查数据,根据数据作出散点图,通过拟合函数图象,求出可以近似表示变化规律的函数模型,进一步用函数模型来解决问题。
课堂小结
现实问题
现实模型
改造
三角函数模型
抽象 概括
解析式
图形
三角函数模型的解
数学 方法
还原 说明
现实模型的解
是否符合实际 修改
1、一台发电机产生的交流电的电压V和时间t之间关系的图象如下图所示,则电压V和时间t之间的函数解析式为 .
V=536sin100πt,t∈[0,+∞)
课堂练习
2、如右上图,单摆从某点开始来回摆动,离开平衡位置O的距离s cm和时间t s的函数关系式为s=6sin(2πt+ ),那么单摆来回摆动一次所需的时间为( )
A.2π s
C.0.5s
B.πs
D.1s
D
3、已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位:时)的函数,记做
下表是某日各时的浪高数据:
t 0 3 6 9 12 15 18 21 24
y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,
的曲线可近似地看成是函数
(2)依据规定,当海浪高度不低于1米时才对冲浪爱好者开放,请根据(1)的结论,判断一天内的上午8:00至18:00时这段时间内,有______个小时可供冲浪爱好者进行运动。
6
(1)根据以上数据,写出函数
的函数表达式____________。
4、如图,摩天轮的半径为50m,圆心O点距地面的高度为60m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处,已知在时刻t(min)时点P距离地面的高度
(II)求证:不论t为何值时
为定值。
(I)求在2006min时点P距离地面的高度;
解:(I)由题意可知:
即
又
得
即点P距离地面的高度为85m。
(II)由(I)知
故不论t为何值,都是定值。
