2019-2020学年高中数学选修1-2第三章推理与证明 §2 数学证明课件:51张PPT
文档属性
| 名称 | 2019-2020学年高中数学选修1-2第三章推理与证明 §2 数学证明课件:51张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 564.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 15:59:08 | ||
图片预览










文档简介
课件51张PPT。第三章推理与证明§2 数学证明自主预习学案从前,有一个懒人得到一大瓮的米,便开始想入非非:“如果我卖掉这些米,用卖米的钱买来尽可能多的小鸡,这些小鸡长大后会下很多蛋,然后我把鸡和蛋卖了,再买来许多猪,当这些猪长大的时候,便会生许多小猪,等小猪长大后再把它们全卖了,我就有钱买一块地了,有了地便可以种甘蔗和谷物,有了收成,我就可以买更多的地,再经营几年,我就能够盖上一幢漂亮的房子,盖好房子后,我将娶一个世上最美的女人做妻子!”懒人兴奋得手舞足蹈,一脚踢翻了米瓮,米落在地上,一大群鸡把米啄食精光,小鸡、猪、土地、房子和妻子,一切的一切都成了泡影,尽管懒人的结局是可悲的,但他的演绎术却值得称道.1.演绎推理
(1)演绎推理
从________________出发,推出____________情况下的结论,我们把这种推理称为演绎推理,简言之,演绎推理是由______________的推理.
(2)演绎推理的特点
①演绎的前提是一般性原理,演绎所得的结论是蕴涵于前提之中的个别、特殊事实,结论完全蕴涵于前提之中.一般性的原理 某个特殊 一般到特殊 ②在演绎推理中,前提与结论之间存在必然的联系.只要前提是真实的,推理的形式是正确的,那么结论也必定是正确的.因而演绎推理是数学中严格证明的工具.
③演绎推理是一种收敛性的思维方法,它缺少创造性,但却具有条理清晰、令人信服的论证作用,有助于科学的理论化和系统化.2.三段论推理
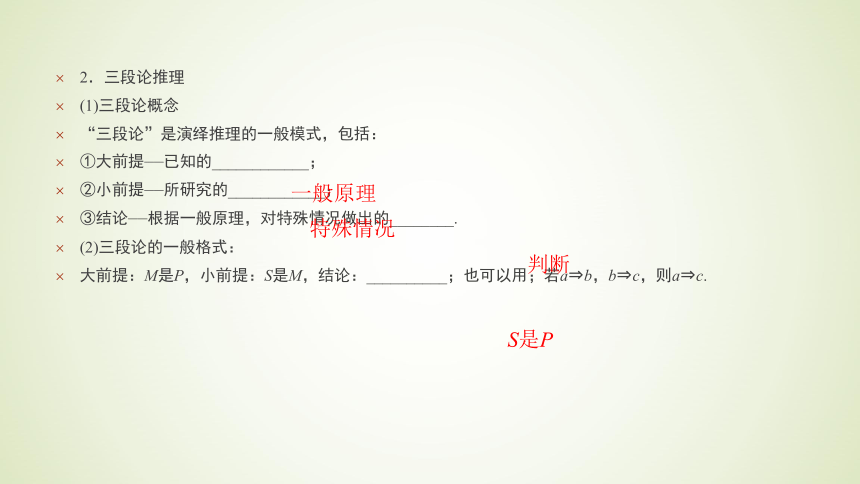
(1)三段论概念
“三段论”是演绎推理的一般模式,包括:
①大前提——已知的____________;
②小前提——所研究的____________;
③结论——根据一般原理,对特殊情况做出的________.
(2)三段论的一般格式:
大前提:M是P,小前提:S是M,结论:__________;也可以用;若a?b,b?c,则a?c.一般原理 特殊情况 判断 S是P (3)三段论法的论断基础是这样一个公理:“凡肯定(或否定)了某一类对象的全部,也就肯定(或否定)了这一类对象的各部分或个体”,简言之,“全体概括个体”.M、P、S三个概念之间的包含关系表现为:如果概念P包含了概念M,则必包含了M中的任一概念S,如图,如果概念P排斥概念M,则必排斥M中的任一概念S.(4)在演绎推理中,前提与结论之间存在必然的联系,只要前提是真实的,推理的形式是正确的,那么________必定是正确的.因而演绎推理是数学中严格证明的工具,而合情推理的结论__________正确.
为了方便,在运用三段论推理时,常常采用省略大前提或小前提的表述方式.对于复杂的论证,总是采用一连串的三段论,把前一个三段论的________作为下一个三段论的前提.结论 不一定 结论 1.合情推理与演绎推理的区别
(1)推理一般包括合情推理与演绎推理.合情推理包括归纳推理和类比推理.归纳是由特殊到一般的推理,类比是由特殊到特殊的推理,而演绎推理是由一般到特殊的推理.
(2)合情推理是根据已有的事实和正确的结论(包括定义、公理、定理等),实验和实践的结果,以及个人的经验和直觉等推测某些结果的推理过程,归纳和类比是合情推理常用的方法.在解决问题的过程中,合情推理具有猜测和发现结论、探索和提供思路的作用.有利于创新意识的培养.演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等)按照严格的逻辑法则得到新结论的推理过程,培养和提高演绎推理或逻辑证明的能力是高中课程的重要目标.
(3)从推理的结论来看,合情推理的结论不一定正确,有待证明;演绎推理在前提和推理形式正确的前提下得到的结论一定正确.2.合情推理与演绎推理的联系
(1)数学发现过程是一个探索创造的过程,是一个不断地提出猜想、验证、猜想的过程,合情推理和演绎推理相辅相成,相互作用,共同推动着发现活动的进程.数学结论、证明思路的发现,主要靠合情推理.而演绎推理是证明数学结论、建立数学体系的重要思维过程.
(2)合情推理是富于创造性的推理,在数学发现活动中,它为演绎推理确定了目标和方向,具有提出猜想、发现结论、提供思路的作用.演绎推理是形式化程度较高的必然推理,为合情推理提供了前提,为探索活动提供了依据.1.演绎推理是( )
A.部分到整体,个别到一般的推理
B.特殊到特殊的推理
C.一般到特殊的推理
D.一般到一般的推理
[解析] 演绎推理是由一般到特殊的推理.C2.“所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数.”上述推理( )
A.小前提错 B.结论错
C.正确 D.大前提错
[解析] 9=3×3,所以大前提是正确的,又小前提和推理过程都正确,所以结论也正确,故上述推理正确.CB
[解析] 求证:“a大前提:因为在三角形中,大角对大边,
小前提:∠A=30°,∠B=60°,则∠A<∠B,
结论:所以a故证明画线部分是演绎推理的小前提,故选B.m“因为过不共线的三点有且仅有一个平面(大前提),而A、B、C为空间三点(小前提),所以过A、B、C三点只能确定一个平面(结论).”
[解析] 不正确,因为大前提中的“三点”不共线,而小前提中的“三点”没有不共线的限制条件.互动探究学案命题方向1 ?把演绎推理写成三段论形式[思路分析] 首先分析出每个题的大前提、小前提及结论,再写成三段论的形式.
[解析] (1)向量是既有大小又有方向的量,大前提
零向量是向量,小前提
所以零向量也有大小和方向.结论
(2)每一个矩形的对角线都相等,大前提
正方形是矩形,小前提
正方形的对角线相等.结论『规律方法』 1.分析演绎推理的构成时,要正确区分大前提、小前提、结论,省略大前提的要补出来.
2.判断演绎推理是否正确的方法
(1)看推理形式是否为由一般到特殊的推理,只有由一般到特殊的推理才是演绎推理,这是最易出错的地方;
(2)看大前提是否正确,大前提往往是定义、定理、性质等,注意其中有无前提条件;
(3)看小前提是否正确,注意小前提必须在大前提范围之内;
(4)看推理过程是否正确,即看由大前提,小前提得到的结论是否正确.〔跟踪练习1〕
指出下列推理中的错误,并分析产生错误的原因:
(1)整数是自然数,大前提
-3是整数,小前提
-3是自然数.结论
(2)常函数的导函数为0,大前提
函数f(x)的导函数为0,小前提
f(x)为常函数.结论命题方向2 ?三段论在证明几何问题中的应用[解析] ∵等腰三角形两底角相等,大前提
△ADC是等腰三角形,∠1和∠2是两个底角,小前提
∴∠1=∠2.结论
∵两条平行线被第三条直线截得的内错角相等,大前提
∠1和∠3是平行线AD、BC被AC截得的内错角,小前提
∴∠1=∠3.结论
∵等于同一个角的两个角相等,大前提
∠2=∠1,∠3=∠1,小前提
∴∠2=∠3,即AC平分∠BCD.结论『规律方法』 应用演绎推理证明时,必须确切知道每一步推理的依据(大前提),验证条件是否满足(小前提),然后得出结论.〔跟踪练习2〕
用三段论的形式写出下列演绎推理.
(1)菱形的对角线相互垂直,正方形是菱形,所以正方形的对角线相互垂直.
(2)若两角是对顶角,则此两角相等,所以若两角不相等,则此两角不是对顶角.
[分析] 即写出推理的大前提、小前提、结论.大前提可能在题目中给出,也可能是已经学过的知识.[解析] (1)每个菱形的对角线都相互垂直大前提
正方形是菱形小前提
正方形的对角线相互垂直结论
(2)若两个角是对顶角则两角相等大前提
∠1和∠2不相等小前提
∠1和∠2不是对顶角结论命题方向3 ?演绎推理在代数问题中的应用『规律方法』 在几何、代数证题过程中,如果每一次都按三段论写出解答过程会很繁琐,也不必要.因此实际证题中,那些公认的简单事实,已知的公理、定理等大前提条件可以省略,那些前面证得的结论也可省略,但必须要保证证题过程的严密规范.不要张冠李戴 [辨析] 错误的原因在于虽然运用的大前提正确,即在同一个三角形中,大边对大角,但AD与BD并不是在同一个三角形内的两条边,即小前提不成立,所以推理过程错误.
[正解] 因为CD⊥AB,所以∠ADC=∠BDC=90°,
所以∠A+ACD=∠B+∠BCD=90°,
在△ABC中,AC>BC,∴∠B>∠A,
∴∠ACD>∠BCD.〔跟踪练习4〕
若数列{an}的首项为a1,且满足从第三项起,每一项与前一项的和都是同一个常数s,求数列{an}的通项公式.演绎推理的综合应用 已知函数f(x),对任意x,y∈R都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(1)=-2.
(1)求证f(x)是奇函数;
(2)求f(x)在[-3,3]上的最大值和最小值.
[解析] (1)证明:因为x,y∈R时,f(x+y)=f(x)+f(y),
所以令x=y=0,得f(0)=f(0)+f(0)=2f(0),
所以f(0)=0.
令y=-x,则f(x-x)=f(x)+f(-x)=0,
所以f(-x)=-f(x),所以f(x)为奇函数.(2)解:设任意的x1,x2∈R且x1f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1),
因为x>0时,f(x)<0,
所以f(x2-x1)<0,即f(x2)-f(x1)<0,
所以f(x)为R上的减函数,
所以f(x)在[-3,3]上的最大值为f(-3),最小值为f(3).
因为f(3)=f(2)+f(1)=3f(1)=-6,
f(-3)=-f(3)=6,
所以函数f(x)在[-3,3]上的最大值为6,最小值为-6.『规律方法』 函数为抽象函数,可借助图像或具体函数辅助理解;(1)奇偶性的判定可利用定义;(2)求函数的最值可利用单调性.1.“π是无限不循环小数,所以π是无理数”,以上推理的大前提是( )
A.实数分为有理数和无理数
B.π不是有理数
C.无限不循环小数都是无理数
D.有理数都是有限循环小数C2.对于推理:若a>b,则a2>b2,因为1>-2,所以12>(-2)2,以下说法中正确的是( )
A.大前提错误 B.小前提错误
C.推理形式错误 D.不是演绎推理
[解析] 大前提:若a>b,则a2>b2是错误的,故选A.A3.由①正方形的对角线相等;②矩形的对角线相等;③正方形是矩形.写一个“三段论”形式的推理,则作为大前提、小前提和结论的分别为( )
A.②①③ B.③①②
C.①②③ D.②③①
[解析] 用三段论的形式写出的演绎推理是:
大前提 ②矩形的四个内角相等
小前提 ③正方形是矩形
结论 ①正方形的四个内角相等
故选D.D5.已知数列{an}满足a1=1,a2=3,an+2=3an+1-2an(n∈N*).
(1)证明:数列{an+1-an}是等比数列.
(2)求数列{an}的通项公式.
(1)演绎推理
从________________出发,推出____________情况下的结论,我们把这种推理称为演绎推理,简言之,演绎推理是由______________的推理.
(2)演绎推理的特点
①演绎的前提是一般性原理,演绎所得的结论是蕴涵于前提之中的个别、特殊事实,结论完全蕴涵于前提之中.一般性的原理 某个特殊 一般到特殊 ②在演绎推理中,前提与结论之间存在必然的联系.只要前提是真实的,推理的形式是正确的,那么结论也必定是正确的.因而演绎推理是数学中严格证明的工具.
③演绎推理是一种收敛性的思维方法,它缺少创造性,但却具有条理清晰、令人信服的论证作用,有助于科学的理论化和系统化.2.三段论推理
(1)三段论概念
“三段论”是演绎推理的一般模式,包括:
①大前提——已知的____________;
②小前提——所研究的____________;
③结论——根据一般原理,对特殊情况做出的________.
(2)三段论的一般格式:
大前提:M是P,小前提:S是M,结论:__________;也可以用;若a?b,b?c,则a?c.一般原理 特殊情况 判断 S是P (3)三段论法的论断基础是这样一个公理:“凡肯定(或否定)了某一类对象的全部,也就肯定(或否定)了这一类对象的各部分或个体”,简言之,“全体概括个体”.M、P、S三个概念之间的包含关系表现为:如果概念P包含了概念M,则必包含了M中的任一概念S,如图,如果概念P排斥概念M,则必排斥M中的任一概念S.(4)在演绎推理中,前提与结论之间存在必然的联系,只要前提是真实的,推理的形式是正确的,那么________必定是正确的.因而演绎推理是数学中严格证明的工具,而合情推理的结论__________正确.
为了方便,在运用三段论推理时,常常采用省略大前提或小前提的表述方式.对于复杂的论证,总是采用一连串的三段论,把前一个三段论的________作为下一个三段论的前提.结论 不一定 结论 1.合情推理与演绎推理的区别
(1)推理一般包括合情推理与演绎推理.合情推理包括归纳推理和类比推理.归纳是由特殊到一般的推理,类比是由特殊到特殊的推理,而演绎推理是由一般到特殊的推理.
(2)合情推理是根据已有的事实和正确的结论(包括定义、公理、定理等),实验和实践的结果,以及个人的经验和直觉等推测某些结果的推理过程,归纳和类比是合情推理常用的方法.在解决问题的过程中,合情推理具有猜测和发现结论、探索和提供思路的作用.有利于创新意识的培养.演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等)按照严格的逻辑法则得到新结论的推理过程,培养和提高演绎推理或逻辑证明的能力是高中课程的重要目标.
(3)从推理的结论来看,合情推理的结论不一定正确,有待证明;演绎推理在前提和推理形式正确的前提下得到的结论一定正确.2.合情推理与演绎推理的联系
(1)数学发现过程是一个探索创造的过程,是一个不断地提出猜想、验证、猜想的过程,合情推理和演绎推理相辅相成,相互作用,共同推动着发现活动的进程.数学结论、证明思路的发现,主要靠合情推理.而演绎推理是证明数学结论、建立数学体系的重要思维过程.
(2)合情推理是富于创造性的推理,在数学发现活动中,它为演绎推理确定了目标和方向,具有提出猜想、发现结论、提供思路的作用.演绎推理是形式化程度较高的必然推理,为合情推理提供了前提,为探索活动提供了依据.1.演绎推理是( )
A.部分到整体,个别到一般的推理
B.特殊到特殊的推理
C.一般到特殊的推理
D.一般到一般的推理
[解析] 演绎推理是由一般到特殊的推理.C2.“所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数.”上述推理( )
A.小前提错 B.结论错
C.正确 D.大前提错
[解析] 9=3×3,所以大前提是正确的,又小前提和推理过程都正确,所以结论也正确,故上述推理正确.CB
[解析] 求证:“a
小前提:∠A=30°,∠B=60°,则∠A<∠B,
结论:所以a
[解析] 不正确,因为大前提中的“三点”不共线,而小前提中的“三点”没有不共线的限制条件.互动探究学案命题方向1 ?把演绎推理写成三段论形式[思路分析] 首先分析出每个题的大前提、小前提及结论,再写成三段论的形式.
[解析] (1)向量是既有大小又有方向的量,大前提
零向量是向量,小前提
所以零向量也有大小和方向.结论
(2)每一个矩形的对角线都相等,大前提
正方形是矩形,小前提
正方形的对角线相等.结论『规律方法』 1.分析演绎推理的构成时,要正确区分大前提、小前提、结论,省略大前提的要补出来.
2.判断演绎推理是否正确的方法
(1)看推理形式是否为由一般到特殊的推理,只有由一般到特殊的推理才是演绎推理,这是最易出错的地方;
(2)看大前提是否正确,大前提往往是定义、定理、性质等,注意其中有无前提条件;
(3)看小前提是否正确,注意小前提必须在大前提范围之内;
(4)看推理过程是否正确,即看由大前提,小前提得到的结论是否正确.〔跟踪练习1〕
指出下列推理中的错误,并分析产生错误的原因:
(1)整数是自然数,大前提
-3是整数,小前提
-3是自然数.结论
(2)常函数的导函数为0,大前提
函数f(x)的导函数为0,小前提
f(x)为常函数.结论命题方向2 ?三段论在证明几何问题中的应用[解析] ∵等腰三角形两底角相等,大前提
△ADC是等腰三角形,∠1和∠2是两个底角,小前提
∴∠1=∠2.结论
∵两条平行线被第三条直线截得的内错角相等,大前提
∠1和∠3是平行线AD、BC被AC截得的内错角,小前提
∴∠1=∠3.结论
∵等于同一个角的两个角相等,大前提
∠2=∠1,∠3=∠1,小前提
∴∠2=∠3,即AC平分∠BCD.结论『规律方法』 应用演绎推理证明时,必须确切知道每一步推理的依据(大前提),验证条件是否满足(小前提),然后得出结论.〔跟踪练习2〕
用三段论的形式写出下列演绎推理.
(1)菱形的对角线相互垂直,正方形是菱形,所以正方形的对角线相互垂直.
(2)若两角是对顶角,则此两角相等,所以若两角不相等,则此两角不是对顶角.
[分析] 即写出推理的大前提、小前提、结论.大前提可能在题目中给出,也可能是已经学过的知识.[解析] (1)每个菱形的对角线都相互垂直大前提
正方形是菱形小前提
正方形的对角线相互垂直结论
(2)若两个角是对顶角则两角相等大前提
∠1和∠2不相等小前提
∠1和∠2不是对顶角结论命题方向3 ?演绎推理在代数问题中的应用『规律方法』 在几何、代数证题过程中,如果每一次都按三段论写出解答过程会很繁琐,也不必要.因此实际证题中,那些公认的简单事实,已知的公理、定理等大前提条件可以省略,那些前面证得的结论也可省略,但必须要保证证题过程的严密规范.不要张冠李戴 [辨析] 错误的原因在于虽然运用的大前提正确,即在同一个三角形中,大边对大角,但AD与BD并不是在同一个三角形内的两条边,即小前提不成立,所以推理过程错误.
[正解] 因为CD⊥AB,所以∠ADC=∠BDC=90°,
所以∠A+ACD=∠B+∠BCD=90°,
在△ABC中,AC>BC,∴∠B>∠A,
∴∠ACD>∠BCD.〔跟踪练习4〕
若数列{an}的首项为a1,且满足从第三项起,每一项与前一项的和都是同一个常数s,求数列{an}的通项公式.演绎推理的综合应用 已知函数f(x),对任意x,y∈R都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(1)=-2.
(1)求证f(x)是奇函数;
(2)求f(x)在[-3,3]上的最大值和最小值.
[解析] (1)证明:因为x,y∈R时,f(x+y)=f(x)+f(y),
所以令x=y=0,得f(0)=f(0)+f(0)=2f(0),
所以f(0)=0.
令y=-x,则f(x-x)=f(x)+f(-x)=0,
所以f(-x)=-f(x),所以f(x)为奇函数.(2)解:设任意的x1,x2∈R且x1
因为x>0时,f(x)<0,
所以f(x2-x1)<0,即f(x2)-f(x1)<0,
所以f(x)为R上的减函数,
所以f(x)在[-3,3]上的最大值为f(-3),最小值为f(3).
因为f(3)=f(2)+f(1)=3f(1)=-6,
f(-3)=-f(3)=6,
所以函数f(x)在[-3,3]上的最大值为6,最小值为-6.『规律方法』 函数为抽象函数,可借助图像或具体函数辅助理解;(1)奇偶性的判定可利用定义;(2)求函数的最值可利用单调性.1.“π是无限不循环小数,所以π是无理数”,以上推理的大前提是( )
A.实数分为有理数和无理数
B.π不是有理数
C.无限不循环小数都是无理数
D.有理数都是有限循环小数C2.对于推理:若a>b,则a2>b2,因为1>-2,所以12>(-2)2,以下说法中正确的是( )
A.大前提错误 B.小前提错误
C.推理形式错误 D.不是演绎推理
[解析] 大前提:若a>b,则a2>b2是错误的,故选A.A3.由①正方形的对角线相等;②矩形的对角线相等;③正方形是矩形.写一个“三段论”形式的推理,则作为大前提、小前提和结论的分别为( )
A.②①③ B.③①②
C.①②③ D.②③①
[解析] 用三段论的形式写出的演绎推理是:
大前提 ②矩形的四个内角相等
小前提 ③正方形是矩形
结论 ①正方形的四个内角相等
故选D.D5.已知数列{an}满足a1=1,a2=3,an+2=3an+1-2an(n∈N*).
(1)证明:数列{an+1-an}是等比数列.
(2)求数列{an}的通项公式.
同课章节目录
