2019-2020学年高中北师大版数学选修1-2第四章数系的扩充与复数的引入 第2课时复数的几何意义课件:41张PPT
文档属性
| 名称 | 2019-2020学年高中北师大版数学选修1-2第四章数系的扩充与复数的引入 第2课时复数的几何意义课件:41张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 595.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 15:49:06 | ||
图片预览










文档简介
课件41张PPT。第四章数系的扩充与复数的引入§1 数系的扩充和复数的引入第2课时 复数的几何意义自主预习学案大家知道实数的几何模型是数轴上的点,即实数和数轴上的点建立了一一对应关系,那么复数的几何模型又是怎样的呢?在1806年,德国数学家高斯公布了虚数的图像表示法,即虚数能用平面内的点来表示.在直角坐标系中,横轴上取对应实部a的点A,纵轴上取对应虚部b的点B,通过这两点引平行于坐标轴的直线,它们的交点C就表示复数a+bi,这样就将复数与平面内的点建立了一一对应关系,至此找到了复数的几何模型——平面内的点.以后随着对复数的进一步研究,又将复数与平面内的向量建立了一一对应关系,因此复数就有了另一个几何模型——平面内的向量,并且阐述了复数的几何加法和乘法,从而丰富了内涵,至此复数理论也就较完整地建立起来了。1.复平面与复数的几何意义
(1)复平面的定义
建立了直角坐标系来表示复数的平面叫作复平面,x轴叫作________,y轴叫作________,实轴上的点都表示实数,除了________外,虚轴上的点都表示纯虚数.
(2)复数的几何意义
①每一个复数都由它的________和________唯一确定,当把实部和虚部作为一个有序数对时,就和点的坐标一样,从而可以用点表示复数,因此复数与复平面内的点是____________关系.实轴 虚轴 原点 实部 虚部 一一对应 ②若复数z=a+bi(a、b∈R),则其对应的点的坐标是______________,不是(a,bi).
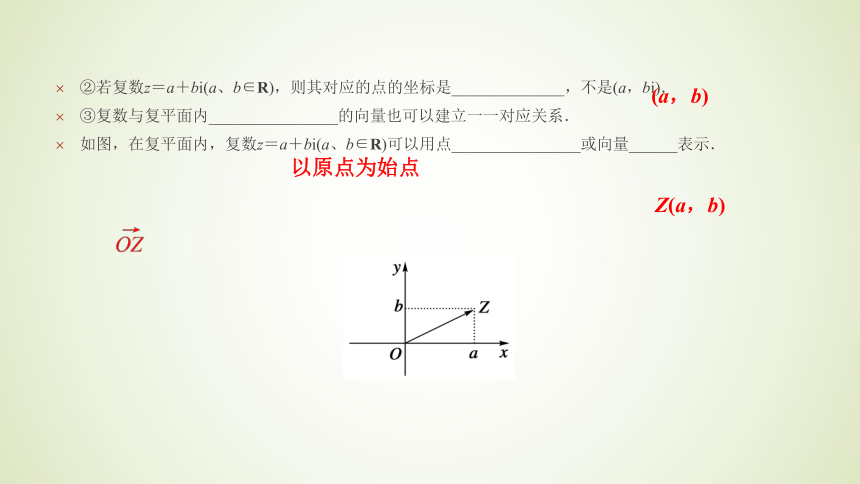
③复数与复平面内________________的向量也可以建立一一对应关系.
如图,在复平面内,复数z=a+bi(a、b∈R)可以用点________________或向量______表示.(a,b) 以原点为始点 Z(a,b) 1.复平面的几个注意点
(1)直角坐标平面可表示复平面,形式上不做改变,要注意纵轴仍然是用y表示,不要认为是yi.
(2)复平面内的点与复数的关系B1.已知a、b∈R,那么在复平面内对应于复数a-bi,-a-bi的两个点的位置关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=x对称
[解析] 在复平面内对应于复数a-bi,-a-bi的两个点为(a,-b)和(-a,-b)关于y轴对称.2.设复数z=a+bi对应的点在虚轴右侧,则( )
A.a>0,b>0 B.a>0,b<0
C.b>0,a∈R D.a>0,b∈R
[解析] 复数对应的点在虚轴右侧,则该复数的实部大于零,虚部可为任意实数.D3.已知复数z=(m-3)+(m-1)i的模等于2,则实数m的值为__________.
A.1或3 B.1
C.3 D.21或3 互动探究学案命题方向1 ?复数的几何意义
[思路分析] 把点的对应关系转化为实部与虚部应满足的条件,求出参数m的值,即得复数z.
[解析] (1)若复数z对应的点在虚轴上(不包括原点),则m2+2m-8=0且m2-3m+2≠0,
∴m=-4,此时z=30i.『规律方法』 1.复数的几何意义包含两种:
(1)复数与复平面内点的对应关系:每一个复数和复平面内的一个点对应,复数的实部、虚部分别是对应点的横坐标、纵坐标.
(2)复数与复平面内向量的对应关系:当向量的起点在原点时,该向量可由终点唯一确定,从而可与该终点对应的复数建立一一对应关系,借助平面向量的有关知识,能更好地理解复数的相关知识.
2.有关复数在复平面内的对应点位置(在实轴上、虚轴上、某个象限内、某条已知直线上等)的题目,先找出复数的实部、虚部,再按点所在的位置列方程或不等式(组)求解.〔跟踪练习1〕
(2019·北京昌平区新学道临川中学月考)在复平面内,复数6+5i,-2+3i对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是( )
A.4+8i B.8+2i
C.2+4i D.4+i
[解析] 由题意知A(6,5),B(-2,3),∴C(2,4),∴点C对应的复数为2+4i,故选C.C命题方向2 ?复数与复平面内向量的对应
〔跟踪练习2〕
(2019·广东江门高二期末)ABCD是复平面内的平行四边形,A,B,C三点对应的复数分别是1+3i,-i,2+i.
(1)求点D对应的复数;
(2)求△ABC的边BC上的高.命题方向3 ?复数模的计算『规律方法』 计算复数的模时,应先找出复数的实部和虚部,然后利用模的公式进行计算.两个虚数不能比较大小 ,但它们的模可以比较大小.D 准确掌握复数模的几何意义 A [错解] 由题意可知(|z|-3)(|z|+1)=0,即|z|=3或|z|=-1,故选D.
[辨析] 错解中忽视了“|z|”的几何意义是“点Z到坐标原点的距离”导致错误.
[正解] A 由题意可知(|z|-3)(|z|+1)=0,即|z|=3或|z|=-1.
∵|z|≥0,∴|z|=-1应舍去,故应选A.〔跟踪练习4〕
已知x是实数,y是纯虚数,且满足(2x-1)+(3-y)i=y-i,求x和y的值.复数与其他知识的综合问题 『规律方法』 利用复数相等的充要条件,将复数问题转化为实数问题来解决.在解题过程中要注意的是:一般由一个复数等式可转化为一个实数方程组,所求出的解要同时满足每一个方程.1.复数z=-1-2i(i为虚数单位)在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
[解析] 复数z=-1-2i在复平面内对应的点为(-1,-2),故选C.C2.复数z=(a2-2a)+(a2-a-2)i对应的点在虚轴上,则( )
A.a≠2或a≠1 B.a≠2或a≠-1
C.a=2或a=0 D.a=0CC C
(1)复平面的定义
建立了直角坐标系来表示复数的平面叫作复平面,x轴叫作________,y轴叫作________,实轴上的点都表示实数,除了________外,虚轴上的点都表示纯虚数.
(2)复数的几何意义
①每一个复数都由它的________和________唯一确定,当把实部和虚部作为一个有序数对时,就和点的坐标一样,从而可以用点表示复数,因此复数与复平面内的点是____________关系.实轴 虚轴 原点 实部 虚部 一一对应 ②若复数z=a+bi(a、b∈R),则其对应的点的坐标是______________,不是(a,bi).
③复数与复平面内________________的向量也可以建立一一对应关系.
如图,在复平面内,复数z=a+bi(a、b∈R)可以用点________________或向量______表示.(a,b) 以原点为始点 Z(a,b) 1.复平面的几个注意点
(1)直角坐标平面可表示复平面,形式上不做改变,要注意纵轴仍然是用y表示,不要认为是yi.
(2)复平面内的点与复数的关系B1.已知a、b∈R,那么在复平面内对应于复数a-bi,-a-bi的两个点的位置关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=x对称
[解析] 在复平面内对应于复数a-bi,-a-bi的两个点为(a,-b)和(-a,-b)关于y轴对称.2.设复数z=a+bi对应的点在虚轴右侧,则( )
A.a>0,b>0 B.a>0,b<0
C.b>0,a∈R D.a>0,b∈R
[解析] 复数对应的点在虚轴右侧,则该复数的实部大于零,虚部可为任意实数.D3.已知复数z=(m-3)+(m-1)i的模等于2,则实数m的值为__________.
A.1或3 B.1
C.3 D.21或3 互动探究学案命题方向1 ?复数的几何意义
[思路分析] 把点的对应关系转化为实部与虚部应满足的条件,求出参数m的值,即得复数z.
[解析] (1)若复数z对应的点在虚轴上(不包括原点),则m2+2m-8=0且m2-3m+2≠0,
∴m=-4,此时z=30i.『规律方法』 1.复数的几何意义包含两种:
(1)复数与复平面内点的对应关系:每一个复数和复平面内的一个点对应,复数的实部、虚部分别是对应点的横坐标、纵坐标.
(2)复数与复平面内向量的对应关系:当向量的起点在原点时,该向量可由终点唯一确定,从而可与该终点对应的复数建立一一对应关系,借助平面向量的有关知识,能更好地理解复数的相关知识.
2.有关复数在复平面内的对应点位置(在实轴上、虚轴上、某个象限内、某条已知直线上等)的题目,先找出复数的实部、虚部,再按点所在的位置列方程或不等式(组)求解.〔跟踪练习1〕
(2019·北京昌平区新学道临川中学月考)在复平面内,复数6+5i,-2+3i对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是( )
A.4+8i B.8+2i
C.2+4i D.4+i
[解析] 由题意知A(6,5),B(-2,3),∴C(2,4),∴点C对应的复数为2+4i,故选C.C命题方向2 ?复数与复平面内向量的对应
〔跟踪练习2〕
(2019·广东江门高二期末)ABCD是复平面内的平行四边形,A,B,C三点对应的复数分别是1+3i,-i,2+i.
(1)求点D对应的复数;
(2)求△ABC的边BC上的高.命题方向3 ?复数模的计算『规律方法』 计算复数的模时,应先找出复数的实部和虚部,然后利用模的公式进行计算.两个虚数不能比较大小 ,但它们的模可以比较大小.D 准确掌握复数模的几何意义 A [错解] 由题意可知(|z|-3)(|z|+1)=0,即|z|=3或|z|=-1,故选D.
[辨析] 错解中忽视了“|z|”的几何意义是“点Z到坐标原点的距离”导致错误.
[正解] A 由题意可知(|z|-3)(|z|+1)=0,即|z|=3或|z|=-1.
∵|z|≥0,∴|z|=-1应舍去,故应选A.〔跟踪练习4〕
已知x是实数,y是纯虚数,且满足(2x-1)+(3-y)i=y-i,求x和y的值.复数与其他知识的综合问题 『规律方法』 利用复数相等的充要条件,将复数问题转化为实数问题来解决.在解题过程中要注意的是:一般由一个复数等式可转化为一个实数方程组,所求出的解要同时满足每一个方程.1.复数z=-1-2i(i为虚数单位)在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
[解析] 复数z=-1-2i在复平面内对应的点为(-1,-2),故选C.C2.复数z=(a2-2a)+(a2-a-2)i对应的点在虚轴上,则( )
A.a≠2或a≠1 B.a≠2或a≠-1
C.a=2或a=0 D.a=0CC C
同课章节目录
