2019-2020学年高中北师大版数学选修1-2第四章数系的扩充与复数的引入 第1课时 复数的加法与减法 课件:46张PPT
文档属性
| 名称 | 2019-2020学年高中北师大版数学选修1-2第四章数系的扩充与复数的引入 第1课时 复数的加法与减法 课件:46张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 803.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 15:49:20 | ||
图片预览










文档简介
课件46张PPT。第四章数系的扩充与复数的引入§2 复数的四则运算第1课时 复数的加法与减法自主预习学案加法是一种累积,使人从小到大,从弱到强,从单纯走向复杂;减法是一种删节,在经过一定的积累以后,删去多余的枝枝叶叶,以化解心灵的重负;乘法是一种跨越,是实现人生跨越的秘诀;除法是一种卸载,一切不道德的尘埃,必须依靠理性来及时卸载,以剔除心灵的稗种.这就是人生的四则运算。
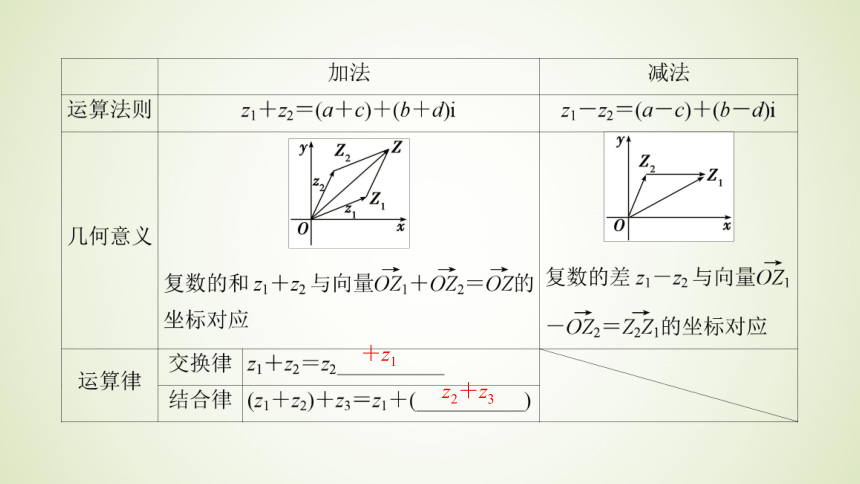
复数作为数系大家庭的一员,它的四则运算又是怎样的呢?复数的加、减法法则及几何意义与运算律+z1 z2+z3 复数的加法的几个注意点
(1)复数的代数形式的加法运算法则是一种规定,以后就按规定进行运算.
(2)复数加法中的规定,是实部与实部相加,虚部与虚部相加.很明显,两个复数的和仍然是一个复数.
(3)复数的加法法则可以推广到多个复数相加的情形.
(4)实数加法的交换律、结合律在复数集C中仍然成立.
(5)复数的代数形式的加法运算法则是一种规定,我们可以从三个方面理解这个规定的合理性:
①当b=0,d=0时,与实数加法法则一致.
②可以验证实数加法运算的交换律和结合律在复数集中仍然成立.
③符合向量加法的平行四边形法则.1.若(1+i)+(2-3i)=a+bi(a、b∈R,i是虚数单位),则a、b的值分别等于( )
A.3,-2 B.3,2
C.3,-3 D.-1,4
[解析] (1+i)+(2-3i)=3-2i,解得a=3,b=-2.AC 3.若复数z1=-2+i,z2=1+2i,则复数z1-z2在复平面内对应点所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
[解析] z1-z2=(-2+i)-(1+2i)=(-2-1)+(i-2i)=-3-i,故z1-z2对应点的坐标为(-3,-1)在第三象限.CA 5.已知|z|=4,且z+2i是实数,则复数z=________________.互动探究学案命题方向1 ?复数代数形式的加减运算[思路分析] 解答本题可根据复数加减运算的法则进行.『规律方法』 复数的加减法运算就是把复数的实部与实部,虚部与虚部分别相加减.〔跟踪练习1〕
复数z1=a2-2-3ai,z2=a+(a2+2)i,若z1+z2是纯虚数,求a.命题方向2 ?复数加、减法运算的几何意义『规律方法』 1.对于一些较复杂的复数运算问题,特别是与复数的模有关的问题可将复数与复平面内以原点为起点的向量加以转化,利用几何意义给予几何解释,数形结合解决.
2.若几何图形的变换可以坐标化,可利用向量、点与复数的关系转化为数的运算处理.
例如关系式|z1+z2|=|z1-z2|的几何解释为:平行四边形两对角线长相等,故四边形OACB为矩形.〔跟踪练习2〕复数z1=1+2i,z2=-2+i,z3=-1-2i,它们在复平面上的对应点分别是一个正方形的三个顶点A、B、C,如图所示,求这个正方形ABCD的第四个顶点D对应的复数.命题方向3 ?复数加减法的综合问题『规律方法』 1.设出复数z=x+yi(x,y∈R),利用复数相等或模的概念,可把条件转化为x、y满足的关系式,利用方程思想求解,这是本章“复数问题实数化思想”的应用.
2.在复平面内,z1,z2对应的点为A、B,z1+z2对应的点为C,O为坐标原点,则四边形OACB:
(1)为平行四边形;(2)若|z1+z2|=|z1-z2|,则四边形OACB为矩形;(3)若|z1|=|z2|,则四边形OACB为菱形;(4)若|z1|=|z2|且|z1+z2|=|z1-z2|,则四边形OACB为正方形.考虑问题要全面 [辨析] 四个点A、B、C、D构成平行四边形,并不仅有□ABCD一种情况,应该还有□ABDC和□ACBD两种情况.如图所示.
[正解] 用错解可求D对应的复数为1-7i,用相同的方法可求得另两种情况下点D对应的复数z.
图①中点D对应的复数为3+7i,
图②中点D对应的复数为-11+3i.
故点D对应的复数为1-7i或3+7i或-11+3i.-4 复数的模的取值范围问题 二审结论,明确解题方向,求|z1+z2|的取值范围,可利用复数运算法则及模的定义转化为求三角函数值域,要特别注意求值域时x的取值范围不能认定就是[0,2π).
第二步,建立联系,确定解题步骤.
由条件与结论之间的关系,确定本题解题步骤:先求x的取值范围,再将|z1+z2|表达为x的三角函数,然后化为一角一函形式,利用三角函数的值域求|z1+z2|的取值范围.
第三步,规范解答.1.复数(1-i)-(2+i)+3i等于( )
A.-1+i B.1-i
C.i D.-i
[解析] (1-i)-(2+i)+3i=(1-2)+(-1-1+3)i=-1+i,故选A.AA 3.[(a-b)-(a+b)i]-[(a+b)-(a-b)i]等于( )
A.-2b-2bi B.-2b+2bi
C.-2a-2bi D.-2a-2ai
[解析] 原式=[(a-b)-(a+b)]+[-(a+b)+(a-b)]i
=-2b-2bi.A
4.复数(1-i)-(2+i)+(4-i)+3i=______.
[解析] (1-i)-(2+i)+(4-i)+3i=1-i-2-i+4-i+3i=(1-2+4)+(-i-i-i+3i)=3.3 因为z1+z2是虚数,
所以m2-2m-15≠0,且m≠-2,
所以m≠5,且m≠-3,且m≠-2,
所以m的取值范围是(-∞,-3)∪(-3,-2)∪(-2,5)∪(5,+∞).
复数作为数系大家庭的一员,它的四则运算又是怎样的呢?复数的加、减法法则及几何意义与运算律+z1 z2+z3 复数的加法的几个注意点
(1)复数的代数形式的加法运算法则是一种规定,以后就按规定进行运算.
(2)复数加法中的规定,是实部与实部相加,虚部与虚部相加.很明显,两个复数的和仍然是一个复数.
(3)复数的加法法则可以推广到多个复数相加的情形.
(4)实数加法的交换律、结合律在复数集C中仍然成立.
(5)复数的代数形式的加法运算法则是一种规定,我们可以从三个方面理解这个规定的合理性:
①当b=0,d=0时,与实数加法法则一致.
②可以验证实数加法运算的交换律和结合律在复数集中仍然成立.
③符合向量加法的平行四边形法则.1.若(1+i)+(2-3i)=a+bi(a、b∈R,i是虚数单位),则a、b的值分别等于( )
A.3,-2 B.3,2
C.3,-3 D.-1,4
[解析] (1+i)+(2-3i)=3-2i,解得a=3,b=-2.AC 3.若复数z1=-2+i,z2=1+2i,则复数z1-z2在复平面内对应点所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
[解析] z1-z2=(-2+i)-(1+2i)=(-2-1)+(i-2i)=-3-i,故z1-z2对应点的坐标为(-3,-1)在第三象限.CA 5.已知|z|=4,且z+2i是实数,则复数z=________________.互动探究学案命题方向1 ?复数代数形式的加减运算[思路分析] 解答本题可根据复数加减运算的法则进行.『规律方法』 复数的加减法运算就是把复数的实部与实部,虚部与虚部分别相加减.〔跟踪练习1〕
复数z1=a2-2-3ai,z2=a+(a2+2)i,若z1+z2是纯虚数,求a.命题方向2 ?复数加、减法运算的几何意义『规律方法』 1.对于一些较复杂的复数运算问题,特别是与复数的模有关的问题可将复数与复平面内以原点为起点的向量加以转化,利用几何意义给予几何解释,数形结合解决.
2.若几何图形的变换可以坐标化,可利用向量、点与复数的关系转化为数的运算处理.
例如关系式|z1+z2|=|z1-z2|的几何解释为:平行四边形两对角线长相等,故四边形OACB为矩形.〔跟踪练习2〕复数z1=1+2i,z2=-2+i,z3=-1-2i,它们在复平面上的对应点分别是一个正方形的三个顶点A、B、C,如图所示,求这个正方形ABCD的第四个顶点D对应的复数.命题方向3 ?复数加减法的综合问题『规律方法』 1.设出复数z=x+yi(x,y∈R),利用复数相等或模的概念,可把条件转化为x、y满足的关系式,利用方程思想求解,这是本章“复数问题实数化思想”的应用.
2.在复平面内,z1,z2对应的点为A、B,z1+z2对应的点为C,O为坐标原点,则四边形OACB:
(1)为平行四边形;(2)若|z1+z2|=|z1-z2|,则四边形OACB为矩形;(3)若|z1|=|z2|,则四边形OACB为菱形;(4)若|z1|=|z2|且|z1+z2|=|z1-z2|,则四边形OACB为正方形.考虑问题要全面 [辨析] 四个点A、B、C、D构成平行四边形,并不仅有□ABCD一种情况,应该还有□ABDC和□ACBD两种情况.如图所示.
[正解] 用错解可求D对应的复数为1-7i,用相同的方法可求得另两种情况下点D对应的复数z.
图①中点D对应的复数为3+7i,
图②中点D对应的复数为-11+3i.
故点D对应的复数为1-7i或3+7i或-11+3i.-4 复数的模的取值范围问题 二审结论,明确解题方向,求|z1+z2|的取值范围,可利用复数运算法则及模的定义转化为求三角函数值域,要特别注意求值域时x的取值范围不能认定就是[0,2π).
第二步,建立联系,确定解题步骤.
由条件与结论之间的关系,确定本题解题步骤:先求x的取值范围,再将|z1+z2|表达为x的三角函数,然后化为一角一函形式,利用三角函数的值域求|z1+z2|的取值范围.
第三步,规范解答.1.复数(1-i)-(2+i)+3i等于( )
A.-1+i B.1-i
C.i D.-i
[解析] (1-i)-(2+i)+3i=(1-2)+(-1-1+3)i=-1+i,故选A.AA 3.[(a-b)-(a+b)i]-[(a+b)-(a-b)i]等于( )
A.-2b-2bi B.-2b+2bi
C.-2a-2bi D.-2a-2ai
[解析] 原式=[(a-b)-(a+b)]+[-(a+b)+(a-b)]i
=-2b-2bi.A
4.复数(1-i)-(2+i)+(4-i)+3i=______.
[解析] (1-i)-(2+i)+(4-i)+3i=1-i-2-i+4-i+3i=(1-2+4)+(-i-i-i+3i)=3.3 因为z1+z2是虚数,
所以m2-2m-15≠0,且m≠-2,
所以m≠5,且m≠-3,且m≠-2,
所以m的取值范围是(-∞,-3)∪(-3,-2)∪(-2,5)∪(5,+∞).
同课章节目录
