2019-2020学年高中北师大版数学选修1-2第四章数系的扩充与复数的引入章末整合提升 课件:40张PPT
文档属性
| 名称 | 2019-2020学年高中北师大版数学选修1-2第四章数系的扩充与复数的引入章末整合提升 课件:40张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 627.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 15:50:02 | ||
图片预览



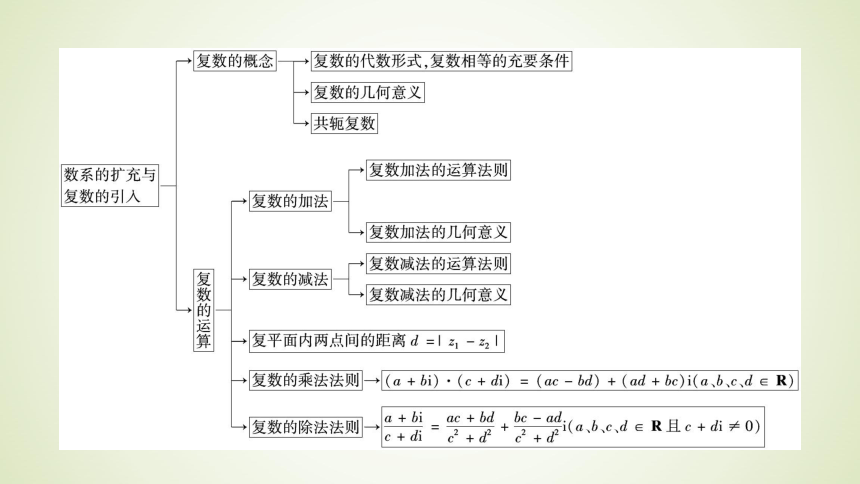








文档简介
课件40张PPT。第四章数系的扩充与复数的引入章末整合提升知 识 网 络知 识 整 合本章在小学、初中和高中所学知识的基础上,介绍复数的概念、复数的代数形式的运算和数系的扩充等内容.
本章共分两大节.第一大节是“数系的扩充与复数的概念”.第二大节是“复数的运算”.在第一大节中,首先简要地展示了数系的扩充过程,回顾了数的发展,并指出当数集扩充到实数集时,由于负数不能开平方,因而大量代数方程无法求解,于是就产生了要开拓新数集的要求,从而自然地引入虚数i,复数由此而产生,接着,介绍了复数的有关概念和复数的几何表示.主要涉及的概念有:复数、虚数、纯虚数、共轭复数、实部、虚部、复数相等、复数的模等.在第二大节中,介绍了复数代数形式的加、减、乘、除的运算法则,同时指出了复数加法、减法的几何意义,复平面上两点间的距离公式,沟通了“数与形”之间的联系,提供了用“形”来帮助处理“数”和用“数”来帮助处理“形”的工具.本章有两条主线:一条主线是以复数代数形式来表示复数的概念.规定了加、乘两种运算法则,然后把减、除法分别定义为加、乘法的逆运算来推导出其运算法则.利用复数的四则运算,可把复数代数形式a+bi看成由a和bi两个非同类项组成,这样多项式的运算法则几乎可以全部搬过来照用不误,于是复数就与多项式、方程联系起来,从而能帮助解决一些多项式中的因式分解、解方程等数学问题.另一条主线是用复平面上的点或向量来描述复数.由此引出了复数运算的几何意义,使复数在平面几何、解析几何中得到广泛应用.这两条主线在教材中是交替安排的,这样能加强学生的“形与数”结合的观念,使学生在看到代数形式时就能联想到几何图形,看到几何图形就能联想到对应的复数.有利于学生深入理解复数概念,开阔学生的思路,培养和提高用“数形结合”观点来处理问题的能力.专 题 突 破熟练掌握复数的代数形式,复数的相等及复数表示各类数的条件是熟练解答复数题的前提.题型一 ?复数的概念复数加、减、乘、除运算的实质是实数的加、减、乘、除,加减法是实部与实部、虚部与虚部分别相加减,而乘法类比多项式乘法,除法类比根式的分母有理化,要注意i2=-1.题型二 ?复数的运算D 复数的几何意义及复数加、减运算的几何意义充分体现了数形结合这一重要的数学思想方法,即通过几何图形来研究代数问题.熟练掌握复平面内的点、以原点为起点的平面向量和复数三者之间的对应关系,就能有效地利用数形转换来解决实际问题.题型三 ?复数及其运算的几何意义D [思路分析] 若z=a+bi(a,b∈R),则z在复平面内的对应点为Z(a,b),据此可由点的坐标写出点对应的复数,也可描出复数在复平面内的对应点.熟记复数模的计算公式和复数的模与以原点为起点的向量的模之间的关系,就能迅速求解有关复数模的问题.题型四 ?复数的模只要掌握共轭复数的定义,会进行简单的运算即可,不必在复数的模与其轭复数的性质上下功夫.题型五 ?共轭复数D 复数是高中数学的重要组成部分,创新是高考的热点之一,给复数定义一个新运算,它既能考查同学们的创新思维,又能考查复数与其他知识的综合.题型六 ?与复数有关的创新型问题D (1)实数x、y、θ有以下关系:x+yi=3+5cosθ+i(-4+5sinθ)(其中i是虚数单位),则x2+y2的最大值为( )
A.30 B.15
C.25 D.100题型七 ?复数与三角函数交汇问题DB C A 3.设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( )
A.-3 B.-2
C.2 D.3
[解析] (1+2i)(a+i)=(a-2)+(2a+1)i,由已知条件,得a-2=2a+1,解得a=-3.故选A.A4.若复数z满足(3-4i)z=5+10i,其中i为虚数单位,则z的虚部为( )
A.-2 B.2
C.-2i D.2iBC 4-i 0 三、解答题
8.实数k分别为何值时,复数(1+i)k2-(3+5i)k-2(2+3i)满足下列条件?
(1)是实数;(2)是虚数;(3)是纯虚数;(4)是0.
[分析] 把复数整理成a+bi(a,b∈R)的形式,用复数分类的条件分别求解.
本章共分两大节.第一大节是“数系的扩充与复数的概念”.第二大节是“复数的运算”.在第一大节中,首先简要地展示了数系的扩充过程,回顾了数的发展,并指出当数集扩充到实数集时,由于负数不能开平方,因而大量代数方程无法求解,于是就产生了要开拓新数集的要求,从而自然地引入虚数i,复数由此而产生,接着,介绍了复数的有关概念和复数的几何表示.主要涉及的概念有:复数、虚数、纯虚数、共轭复数、实部、虚部、复数相等、复数的模等.在第二大节中,介绍了复数代数形式的加、减、乘、除的运算法则,同时指出了复数加法、减法的几何意义,复平面上两点间的距离公式,沟通了“数与形”之间的联系,提供了用“形”来帮助处理“数”和用“数”来帮助处理“形”的工具.本章有两条主线:一条主线是以复数代数形式来表示复数的概念.规定了加、乘两种运算法则,然后把减、除法分别定义为加、乘法的逆运算来推导出其运算法则.利用复数的四则运算,可把复数代数形式a+bi看成由a和bi两个非同类项组成,这样多项式的运算法则几乎可以全部搬过来照用不误,于是复数就与多项式、方程联系起来,从而能帮助解决一些多项式中的因式分解、解方程等数学问题.另一条主线是用复平面上的点或向量来描述复数.由此引出了复数运算的几何意义,使复数在平面几何、解析几何中得到广泛应用.这两条主线在教材中是交替安排的,这样能加强学生的“形与数”结合的观念,使学生在看到代数形式时就能联想到几何图形,看到几何图形就能联想到对应的复数.有利于学生深入理解复数概念,开阔学生的思路,培养和提高用“数形结合”观点来处理问题的能力.专 题 突 破熟练掌握复数的代数形式,复数的相等及复数表示各类数的条件是熟练解答复数题的前提.题型一 ?复数的概念复数加、减、乘、除运算的实质是实数的加、减、乘、除,加减法是实部与实部、虚部与虚部分别相加减,而乘法类比多项式乘法,除法类比根式的分母有理化,要注意i2=-1.题型二 ?复数的运算D 复数的几何意义及复数加、减运算的几何意义充分体现了数形结合这一重要的数学思想方法,即通过几何图形来研究代数问题.熟练掌握复平面内的点、以原点为起点的平面向量和复数三者之间的对应关系,就能有效地利用数形转换来解决实际问题.题型三 ?复数及其运算的几何意义D [思路分析] 若z=a+bi(a,b∈R),则z在复平面内的对应点为Z(a,b),据此可由点的坐标写出点对应的复数,也可描出复数在复平面内的对应点.熟记复数模的计算公式和复数的模与以原点为起点的向量的模之间的关系,就能迅速求解有关复数模的问题.题型四 ?复数的模只要掌握共轭复数的定义,会进行简单的运算即可,不必在复数的模与其轭复数的性质上下功夫.题型五 ?共轭复数D 复数是高中数学的重要组成部分,创新是高考的热点之一,给复数定义一个新运算,它既能考查同学们的创新思维,又能考查复数与其他知识的综合.题型六 ?与复数有关的创新型问题D (1)实数x、y、θ有以下关系:x+yi=3+5cosθ+i(-4+5sinθ)(其中i是虚数单位),则x2+y2的最大值为( )
A.30 B.15
C.25 D.100题型七 ?复数与三角函数交汇问题DB C A 3.设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( )
A.-3 B.-2
C.2 D.3
[解析] (1+2i)(a+i)=(a-2)+(2a+1)i,由已知条件,得a-2=2a+1,解得a=-3.故选A.A4.若复数z满足(3-4i)z=5+10i,其中i为虚数单位,则z的虚部为( )
A.-2 B.2
C.-2i D.2iBC 4-i 0 三、解答题
8.实数k分别为何值时,复数(1+i)k2-(3+5i)k-2(2+3i)满足下列条件?
(1)是实数;(2)是虚数;(3)是纯虚数;(4)是0.
[分析] 把复数整理成a+bi(a,b∈R)的形式,用复数分类的条件分别求解.
同课章节目录
