沪科版七年级数学下册课件7.2.2较复杂的一元一次不等式的解法(16张)
文档属性
| 名称 | 沪科版七年级数学下册课件7.2.2较复杂的一元一次不等式的解法(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 13:38:42 | ||
图片预览




文档简介
课件16张PPT。第七章 一元一次不等式
与不等式组七年级数学沪科版·下册7.2.2 较复杂的一元一次不等式的解法新课引入
用不等式来刻画比 -1大的数为 x >-1. 结合数轴与不等式这两者的相关知识, 我们是否可以将不等式的解集在数轴上通过点用含有方向的线段来表示呢?新知探究
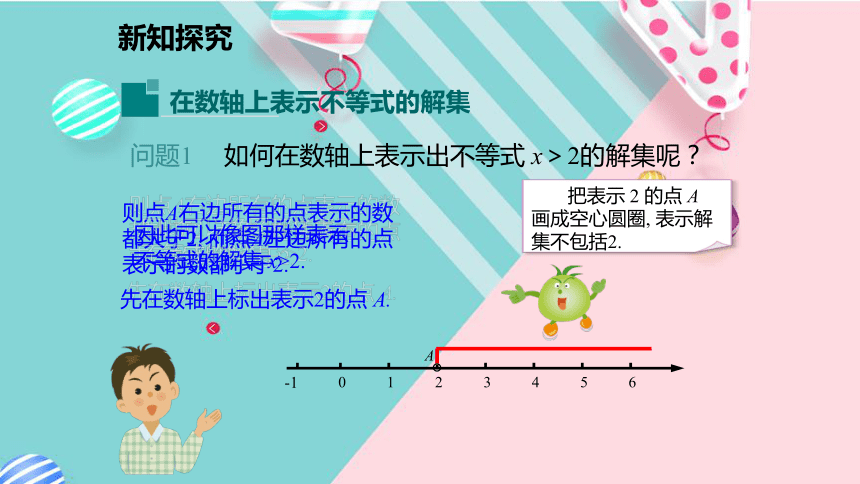
先在数轴上标出表示2的点 A.则点A右边所有的点表示的数都大于2, 而点A左边所有的点表示的数都小于2.因此可以像图那样表示不等式的解集 x>2.问题1 如何在数轴上表示出不等式 x>2的解集呢?A新知探究
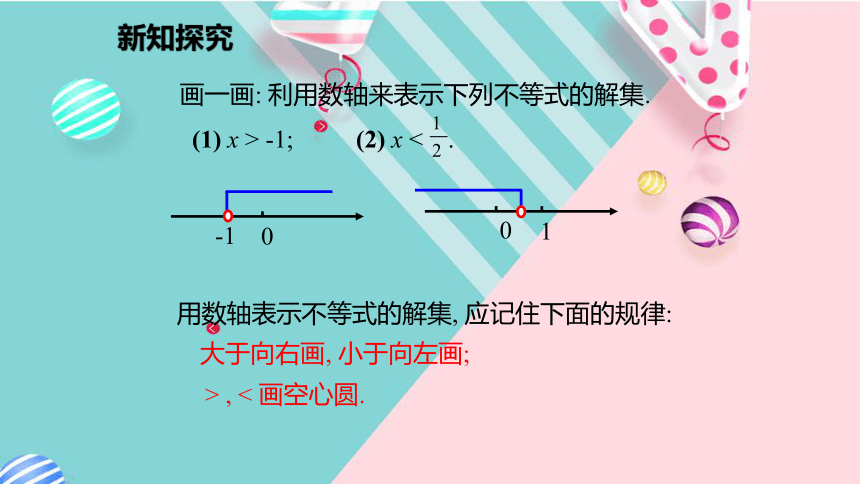
画一画: 利用数轴来表示下列不等式的解集.
(1) x > -1; (2) x < .0-101 用数轴表示不等式的解集, 应记住下面的规律:大于向右画, 小于向左画;> , < 画空心圆.新知探究
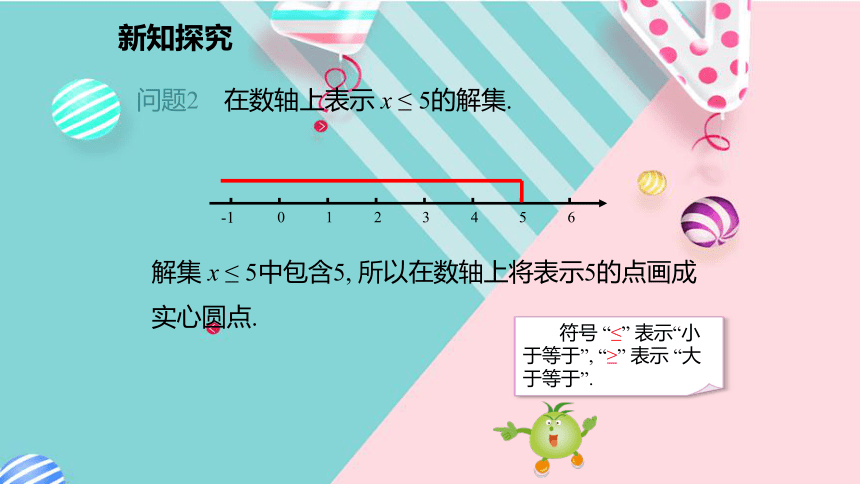
问题2 在数轴上表示 x ≤ 5的解集.解集 x ≤ 5中包含5, 所以在数轴上将表示5的点画成实心圆点.新知探究用数轴表示不等式解集的方法:(1)画数轴;
(2)定边界点: 若这个点包含于解集之中, 则用实心点表示; 不包含在解集中, 则用空心点表示.
(3)定方向: 相对于边界点, 大于向右画, 小于向左画.新知探究例1 解不等式12-6x ≥ 2(1-2x), 并把它的解集在
数轴上表示出来.首先将括号去掉 解: 去括号, 得 12 -6x ≥ 2-4x,移项, 得 -6x+4x ≥ 2-12,将同类项放在一起合并同类项, 得 -2x ≥ -10,两边都除以-2, 得 x ≤ 5.根据不等式基本性质2原不等式的解集在数轴上表示如图所示.注意: x ≤ 5中包含5, 所以在数轴上将表示5的点画成实心圆点.新知探究 在数轴上表示不等式的解集时, 一要把点找准确, 二要找准方向, 三要区别实心圆点与空心圆圈.方法总结新知探究解: 由方程的定义, 把 x=3代入ax+12=0中,
得 a=-4.
把 a=-4代入(a+2)x > -6中,
得-2x > -6,
解得 x < 3.
在数轴上表示如图.
其中正整数解有1和2.例2 已知方程ax+12=0的解是 x=3, 求关于 x不等式
(a+2)x > -6的解集, 并在数轴上表示出来, 其
中正整数解有哪些?新知探究 求不等式的特殊解, 先要准确求出不等式的解集, 然后确定特殊解. 在确定特殊解时, 一定要注意是否包括端点的值, 一般可以结合数轴, 形象直观, 一目了然.方法总结课堂小结解一元一次不等式课堂小测1. 不等式 x >-2与x ≥ -2的解集有什么不同?在数轴上表示它们时怎样区别?分别在数轴上把这两个解集表示出来.课堂小测 2. 用不等式表示图中所示的解集.x<2x ≤ 2x ≥ -7.5课堂小测3. 先用不等式表示下列数量关系, 然后求出它们的解集, 并在数轴上表示出来.课堂小测 (2) y与1的差不大于0;课堂小测 (3) y与5的差大于-2.
用不等式来刻画比 -1大的数为 x >-1. 结合数轴与不等式这两者的相关知识, 我们是否可以将不等式的解集在数轴上通过点用含有方向的线段来表示呢?新知探究
先在数轴上标出表示2的点 A.则点A右边所有的点表示的数都大于2, 而点A左边所有的点表示的数都小于2.因此可以像图那样表示不等式的解集 x>2.问题1 如何在数轴上表示出不等式 x>2的解集呢?A新知探究
画一画: 利用数轴来表示下列不等式的解集.
(1) x > -1; (2) x < .0-101 用数轴表示不等式的解集, 应记住下面的规律:大于向右画, 小于向左画;> , < 画空心圆.新知探究
问题2 在数轴上表示 x ≤ 5的解集.解集 x ≤ 5中包含5, 所以在数轴上将表示5的点画成实心圆点.新知探究用数轴表示不等式解集的方法:(1)画数轴;
(2)定边界点: 若这个点包含于解集之中, 则用实心点表示; 不包含在解集中, 则用空心点表示.
(3)定方向: 相对于边界点, 大于向右画, 小于向左画.新知探究例1 解不等式12-6x ≥ 2(1-2x), 并把它的解集在
数轴上表示出来.首先将括号去掉 解: 去括号, 得 12 -6x ≥ 2-4x,移项, 得 -6x+4x ≥ 2-12,将同类项放在一起合并同类项, 得 -2x ≥ -10,两边都除以-2, 得 x ≤ 5.根据不等式基本性质2原不等式的解集在数轴上表示如图所示.注意: x ≤ 5中包含5, 所以在数轴上将表示5的点画成实心圆点.新知探究 在数轴上表示不等式的解集时, 一要把点找准确, 二要找准方向, 三要区别实心圆点与空心圆圈.方法总结新知探究解: 由方程的定义, 把 x=3代入ax+12=0中,
得 a=-4.
把 a=-4代入(a+2)x > -6中,
得-2x > -6,
解得 x < 3.
在数轴上表示如图.
其中正整数解有1和2.例2 已知方程ax+12=0的解是 x=3, 求关于 x不等式
(a+2)x > -6的解集, 并在数轴上表示出来, 其
中正整数解有哪些?新知探究 求不等式的特殊解, 先要准确求出不等式的解集, 然后确定特殊解. 在确定特殊解时, 一定要注意是否包括端点的值, 一般可以结合数轴, 形象直观, 一目了然.方法总结课堂小结解一元一次不等式课堂小测1. 不等式 x >-2与x ≥ -2的解集有什么不同?在数轴上表示它们时怎样区别?分别在数轴上把这两个解集表示出来.课堂小测 2. 用不等式表示图中所示的解集.x<2x ≤ 2x ≥ -7.5课堂小测3. 先用不等式表示下列数量关系, 然后求出它们的解集, 并在数轴上表示出来.课堂小测 (2) y与1的差不大于0;课堂小测 (3) y与5的差大于-2.
