2.2.2 对数函数及其性质(共34张PPT)
文档属性
| 名称 | 2.2.2 对数函数及其性质(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 15:29:21 | ||
图片预览






文档简介
(共34张PPT)
回顾旧知
还记得得出表达式?
问题
在学习指数函数时,我们引用了细胞分裂的例子,得出分裂个数(y)与分裂次数(x)的函数关系:如下
根据对数定义,将x、y互解,可得到:
改写习惯形式(x→y,y → x),得:
指数函数
是函数吗?
指数函数一般式为:
将x、y互解,可得到:
是函数吗?什么函数?
改写习惯形式(x→y,y → x),得:
知识要点
对数函数定义:
一般地,我们把函数
(a>0,且a≠1)叫做对数函数,其中x是自变量 ,函数的定义域是
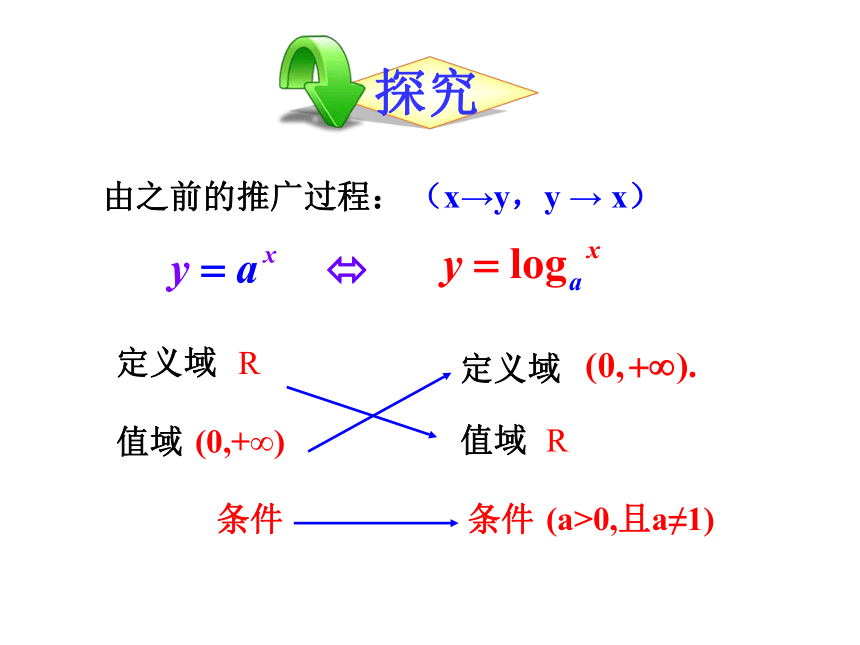
由之前的推广过程:
?
定义域
值域
定义域
值域
条件
条件
R
(a>0,且a≠1)
(x→y,y → x)
R
(0,+∞)
求下列函数的定义域:
解:(1)因为x3>0,即x>0,所以(1)的定义域为{x|x>0};
(2)因为x2-1>0且x2-1≠0,即x>1或x<-1,所以(2)的定义域为{x|x>1或x<-1};
(3)因为9-x2>0,即-33,所以(3)的定义域为{x|-33}.
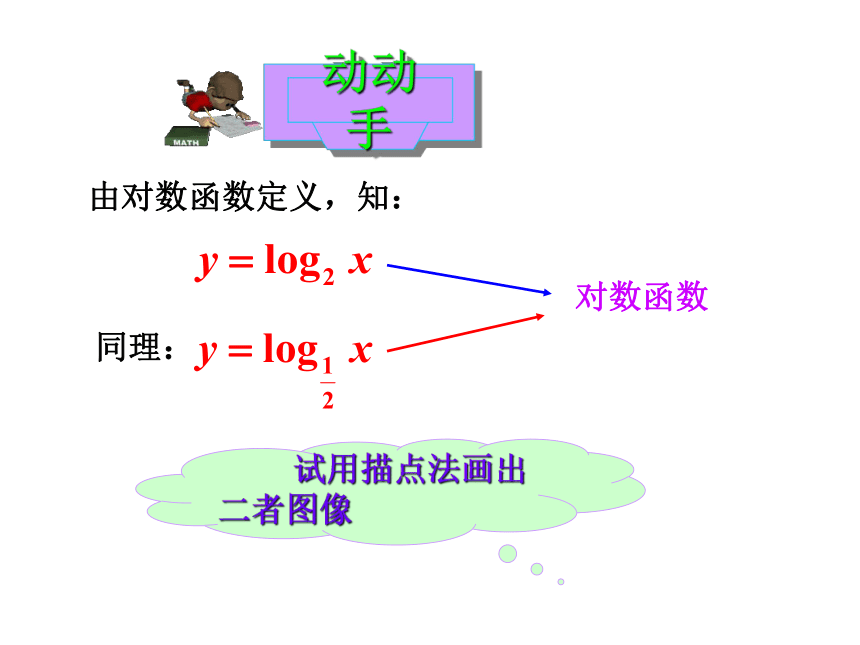
由对数函数定义,知:
对数函数
同理:
试用描点法画出二者图像
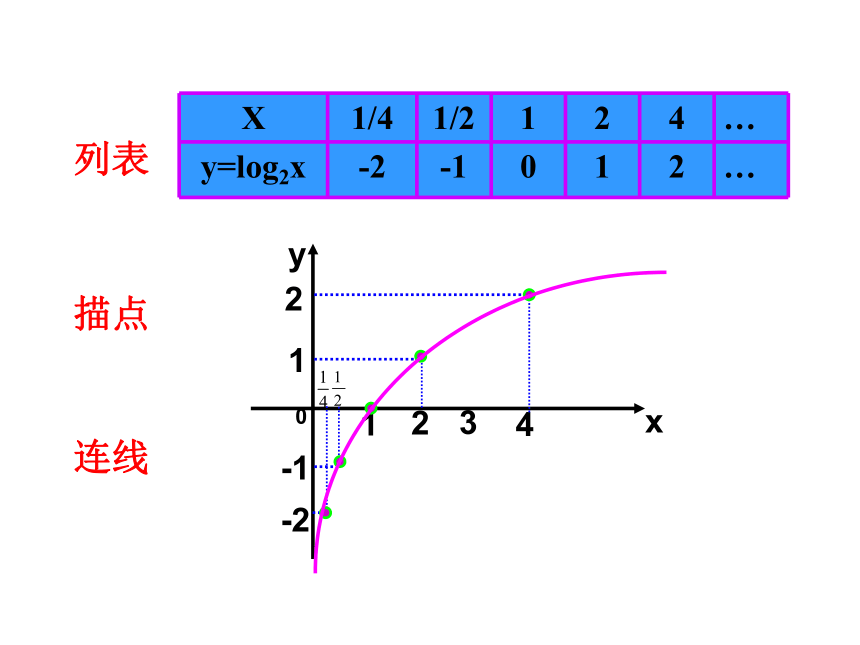
列表
描点
连线
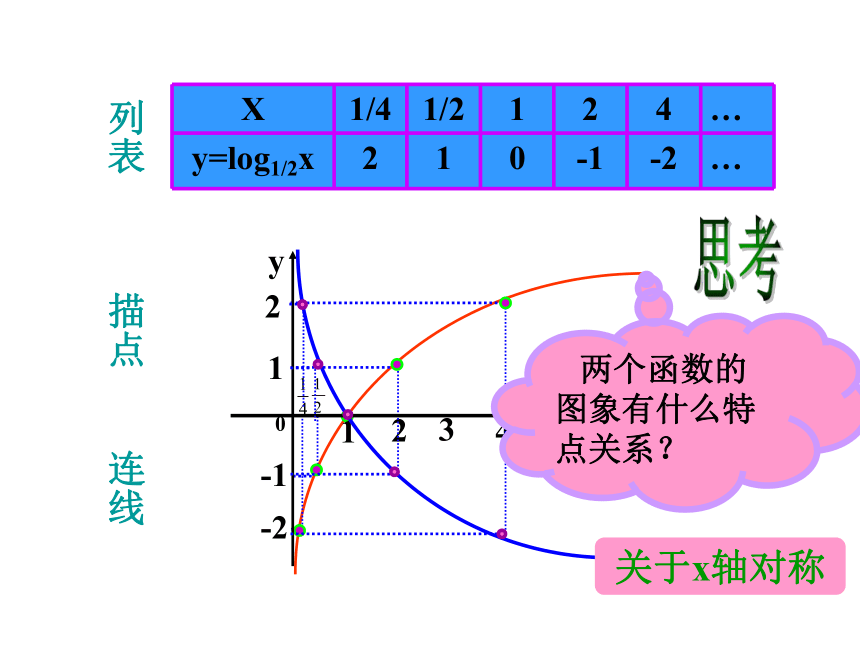
X 1/4 1/2 1 2 4 …
y=log2x -2 -1 0 1 2 …
列表
描点
连线
两个函数的图象有什么特点关系?
关于x轴对称
X 1/4 1/2 1 2 4 …
y=log1/2x 2 1 0 -1 -2 …
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
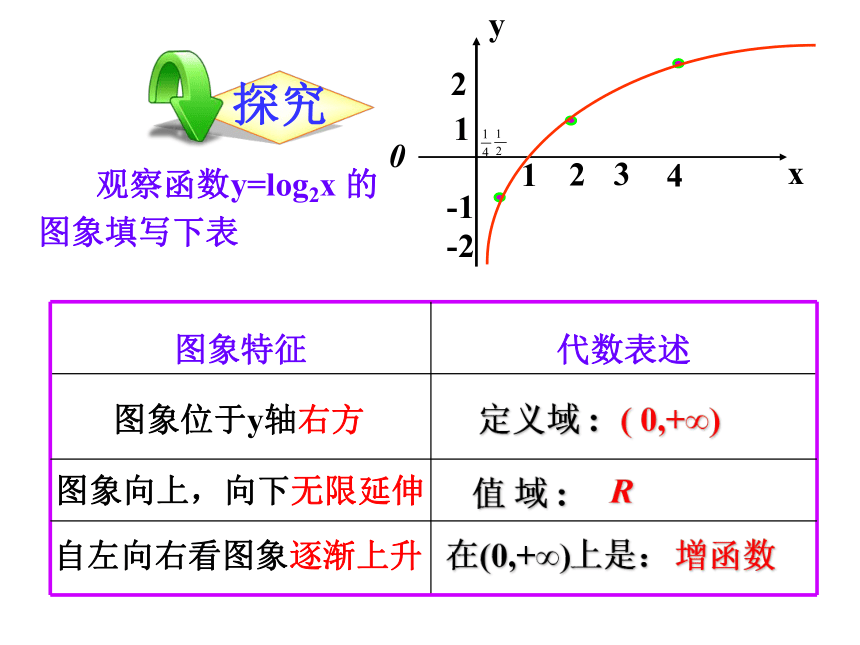
观察函数y=log2x 的图象填写下表
图象位于y轴右方
图象向上,向下无限延伸
自左向右看图象逐渐上升
2
1
-1
-2
1
2
4
0
y
x
3
图象特征 代数表述
观察函数
的图象填写下表
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上,向下无限延伸
自左向右看图象逐渐下降
图象特征 代数表述
知识要点
对数函数图像和性质:
(见下表)
a>1
0 图 象
性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过 点:
( 1, 0 )
x>1,y>0;
x<1, y<0
上增函数
x<1,y>0;
x>1, y<0
上减函数
( 0 , + ∞ )
( 0 , + ∞ )
比较下列各组数中两值的大小:
解:(1)令y=log2x,在(0,+∞)上是增函数,又因为2.5<3.1,所以log22.5< log23.1.
(2)令y=log0.3x,在(0,+∞)上是减函数,又因为2.5<3.1,所以log22.5> log23.1.
(3)当a>1,y=logax,在(0,+∞)上是增函数,又因为2.5<3.1,所以loga2.5< loga3.1.
当0 loga3.1.
比较对数大小——常用方法,如下
1.观察底数是大于1还是小于1;
( a>1时为增函数,02.比较真数值的大小;
3.根据单调性得出结果.
用描点法作出函数
如下:
对比
底数变化时,图像变化趋势?
两两有何对称关系?
当a>1,x轴上方图像自上向下,底数a越来越大.
当0函数y=logax与y=log(1/a)x关于x轴对称.
在问题提出时,我们将
的x、y互解,得到
(x→y,y → x)
习惯做法
?
有什么对应关系?
因为
得来,
是由
(y∈(0,+∞))是
(x∈R)的反函数.
(x→y,y → x)
习惯做法
(y∈(0,+∞))和
(x∈R)互为反函数.
知识要点
对数函数
互为反函数.
和
指数函数
(a>0,且a≠1)
1. 对数函数概念
函数y = logax(a?0,且a ?1)叫做对数函数,其中x是自变量 .函数的定义域是(0,+∞) .
◆方法指导:
研究对数函数时,将a分为a>1和02.指数函数图像
(a>1)
(03.对数函数性质
(1)定义域: 值域:
(2)函数的特殊值:
(3)函数的单调性:
◆方法指导
利用函数图像研究函数性质是一种直观而形象的方法,记忆指数函数性质时可以联想它的图像.
4.比较对数大小——常用方法,如下
(1)观察底数是大于1还是小于1;
(若底数不确定,那就要对底数进行分类讨论);
(2)比较真数值的大小;
(3)根据单调性得出结果.
底数不确定时,那就要对底数进行分类讨论
即0 1
5.指数函数与对数函数之间关系:
说明:
互为反函数的性质
A. x>y>z B. z>y>x C. y>x>z D. z>x>y
C
B
1.求下列函数的定义域:
解:(1)因为(1-x)2>0,即x≠1,所以(1)的定义域为{x|x≠1 };
2.比较下列各组数中两值的大小:
3.比较下列两组数中两值的大小:
借助0或1或中间数进行比较
回顾旧知
还记得得出表达式?
问题
在学习指数函数时,我们引用了细胞分裂的例子,得出分裂个数(y)与分裂次数(x)的函数关系:如下
根据对数定义,将x、y互解,可得到:
改写习惯形式(x→y,y → x),得:
指数函数
是函数吗?
指数函数一般式为:
将x、y互解,可得到:
是函数吗?什么函数?
改写习惯形式(x→y,y → x),得:
知识要点
对数函数定义:
一般地,我们把函数
(a>0,且a≠1)叫做对数函数,其中x是自变量 ,函数的定义域是
由之前的推广过程:
?
定义域
值域
定义域
值域
条件
条件
R
(a>0,且a≠1)
(x→y,y → x)
R
(0,+∞)
求下列函数的定义域:
解:(1)因为x3>0,即x>0,所以(1)的定义域为{x|x>0};
(2)因为x2-1>0且x2-1≠0,即x>1或x<-1,所以(2)的定义域为{x|x>1或x<-1};
(3)因为9-x2>0,即-3
由对数函数定义,知:
对数函数
同理:
试用描点法画出二者图像
列表
描点
连线
X 1/4 1/2 1 2 4 …
y=log2x -2 -1 0 1 2 …
列表
描点
连线
两个函数的图象有什么特点关系?
关于x轴对称
X 1/4 1/2 1 2 4 …
y=log1/2x 2 1 0 -1 -2 …
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
观察函数y=log2x 的图象填写下表
图象位于y轴右方
图象向上,向下无限延伸
自左向右看图象逐渐上升
2
1
-1
-2
1
2
4
0
y
x
3
图象特征 代数表述
观察函数
的图象填写下表
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上,向下无限延伸
自左向右看图象逐渐下降
图象特征 代数表述
知识要点
对数函数图像和性质:
(见下表)
a>1
0
性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过 点:
( 1, 0 )
x>1,y>0;
x<1, y<0
上增函数
x<1,y>0;
x>1, y<0
上减函数
( 0 , + ∞ )
( 0 , + ∞ )
比较下列各组数中两值的大小:
解:(1)令y=log2x,在(0,+∞)上是增函数,又因为2.5<3.1,所以log22.5< log23.1.
(2)令y=log0.3x,在(0,+∞)上是减函数,又因为2.5<3.1,所以log22.5> log23.1.
(3)当a>1,y=logax,在(0,+∞)上是增函数,又因为2.5<3.1,所以loga2.5< loga3.1.
当0
比较对数大小——常用方法,如下
1.观察底数是大于1还是小于1;
( a>1时为增函数,0
3.根据单调性得出结果.
用描点法作出函数
如下:
对比
底数变化时,图像变化趋势?
两两有何对称关系?
当a>1,x轴上方图像自上向下,底数a越来越大.
当0
在问题提出时,我们将
的x、y互解,得到
(x→y,y → x)
习惯做法
?
有什么对应关系?
因为
得来,
是由
(y∈(0,+∞))是
(x∈R)的反函数.
(x→y,y → x)
习惯做法
(y∈(0,+∞))和
(x∈R)互为反函数.
知识要点
对数函数
互为反函数.
和
指数函数
(a>0,且a≠1)
1. 对数函数概念
函数y = logax(a?0,且a ?1)叫做对数函数,其中x是自变量 .函数的定义域是(0,+∞) .
◆方法指导:
研究对数函数时,将a分为a>1和0
(a>1)
(0
(1)定义域: 值域:
(2)函数的特殊值:
(3)函数的单调性:
◆方法指导
利用函数图像研究函数性质是一种直观而形象的方法,记忆指数函数性质时可以联想它的图像.
4.比较对数大小——常用方法,如下
(1)观察底数是大于1还是小于1;
(若底数不确定,那就要对底数进行分类讨论);
(2)比较真数值的大小;
(3)根据单调性得出结果.
底数不确定时,那就要对底数进行分类讨论
即0
5.指数函数与对数函数之间关系:
说明:
互为反函数的性质
A. x>y>z B. z>y>x C. y>x>z D. z>x>y
C
B
1.求下列函数的定义域:
解:(1)因为(1-x)2>0,即x≠1,所以(1)的定义域为{x|x≠1 };
2.比较下列各组数中两值的大小:
3.比较下列两组数中两值的大小:
借助0或1或中间数进行比较
