2.3幂函数(共23张PPT)

(共23张PPT)
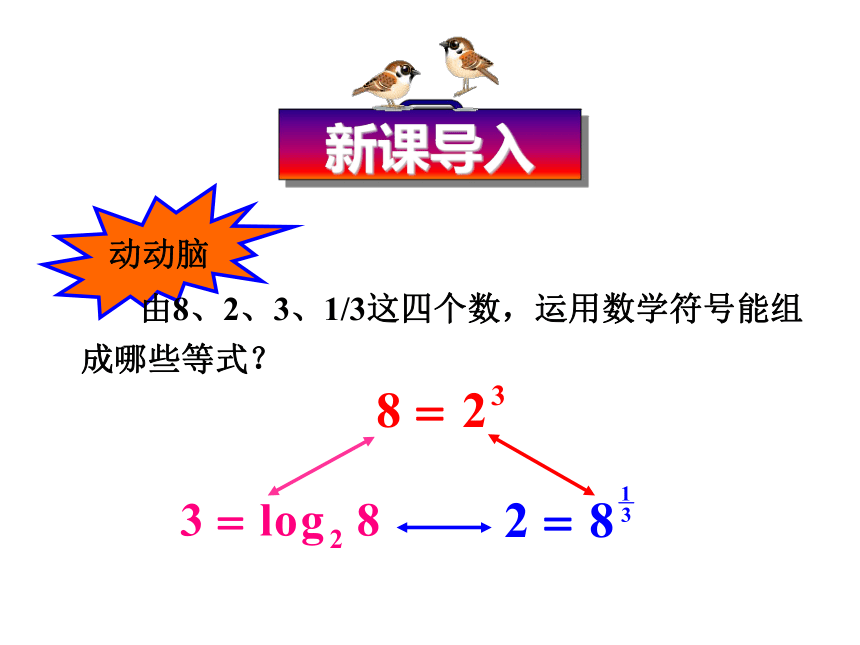
动动脑
由8、2、3、1/3这四个数，运用数学符号能组成哪些等式？
1. 如果a一定，N随b的变化而变化，我们建立了指数函数.
2. 如果a一定，b随N的变化而变化，我们建立了对数函数.
如果b一定，N随a的变化而变化，是不是也应该可以确定一函数？
Y=xb？
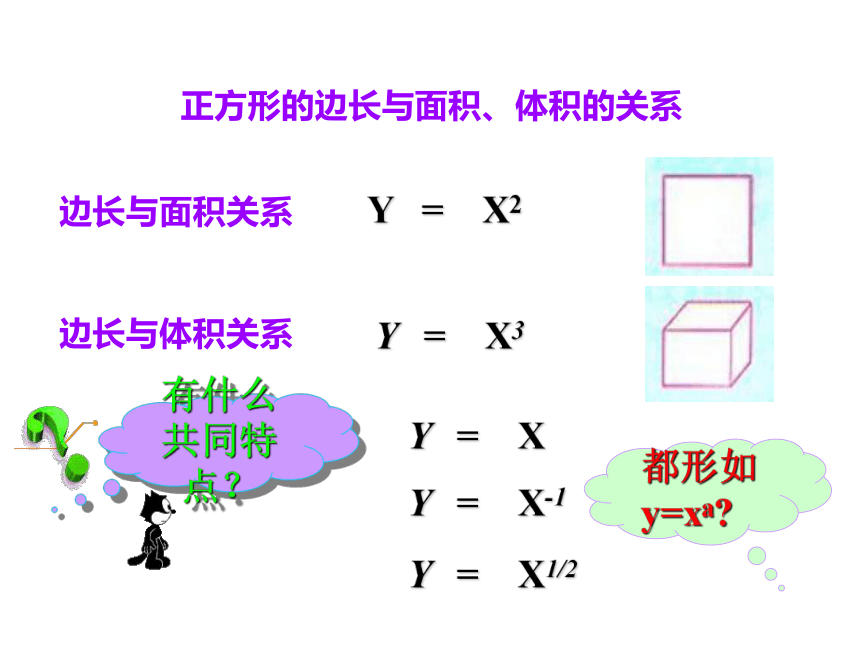
正方形的边长与面积、体积的关系
Y = X2
边长与面积关系
边长与体积关系
Y = X3
Y = X1/2
Y = X-1
Y = X
都形如y=xa?
知识要点
幂函数定义：
一般地，我们把形如 叫做幂函数，其中x是自变量 ， 为常数．(注：我们只研究 =1，2，3，1/2，-1时的情形)
底数
指数
指数
底数
幂值
幂值
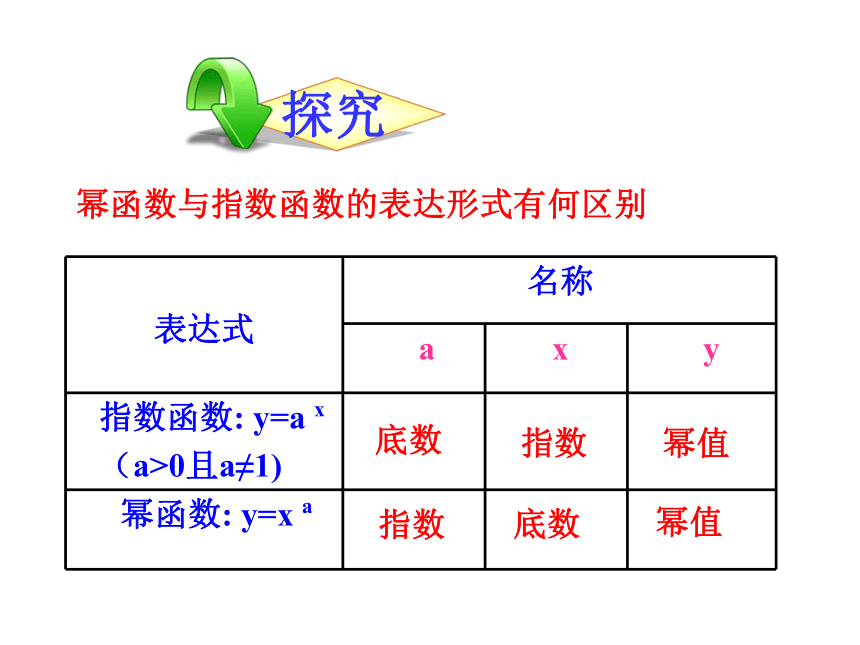
幂函数与指数函数的表达形式有何区别

表达式 名称
a x y
指数函数: y=a x
（a>0且a≠1)
幂函数: y=x a
判断下列函数是否为幂函数．
解：由幂函数的定义得:
(1)是．y=x-2 (2)是．y=x4
(3)不是．指数函数 (4)不是．y=-x4
作出下列幂函数的图象．
y=x2
y=x
y=x3
y=x-1
根据以上图像，得出各自的性质如下：
性质
函数 定义域 值域 奇偶性 单调性 公共点
y=x R R 奇函数 R上递增 (1,1)
y=x2 R [0,+∞) 偶函数 (- ∞,0)减
(0,+ ∞)增 (1,1)
y=x-1 {x|x≠0} {y|y≠0} 奇函数 (- ∞,0)，
(0,+ ∞)减 (1,1)

y＝x1/2 [0,+∞) [0,+∞) 非奇非偶 [0,+∞)增 (1,1)
y=x3 R R 奇函数 R上递增 (1,1)
判断下列函数的奇偶性.
解：由函数奇偶性的定义判断得:
(1) (3) (5) 是奇函数.
(2) 是偶函.
(4) 是非奇非偶函数.
因为函数的奇偶性能够帮助我们完成左半平面内的图象，所以只需要研究它们在第一象限内的图象.
第一象限图像.
图象位置变化，有何规律？
幂函数图象在第一象限的分布情况：
归纳总结
幂函数图象在第一象限的性质：
明白吗？
(B)
判断函数单调性的方法.
记得吗？
作差法或作比较法.
作 f(x1)-f(x2)，或f(x1)/f(x2).
当恒有f(x1)＜f(x2),那么就说f(x)在这个区间上是增函数.
当恒有f(x1)>f(x2).那么就说f(x)在这个区间上是减函数.
设函数f(x)的定义域为I ，在I内某个区间上任取两个自变量x1、x2, 若x11、 幂函数概念
一般地，我们把形如 叫做幂函数，其中x是自变量 ， 为常数.
◆方法指导:
研究幂函数时，我们只研究 ＝1，2，3，－1，1/2的情况.
2、常见5个幂函数图像
y=x2
y=x
y=x3
y=x-1
3、常见5个幂函数性质：
（1）5个基本幂函数的图象都过(1，1)；
（2）函数y＝x，y＝x3，y＝x－1是奇函数，函数y＝x2是偶函数；
（3）在区间(0,+∞)上，函数y＝x，y＝x2，y＝x3，和y＝x1/2是增函数，函数y＝x－1是减函数；
◆方法指导
记忆幂函数性质时可以联想它的图像.
（4）在第一象限内，y＝x－1的图象向上与y轴无限接近；向右与x轴无限接近.
1.判断下列函数是否为幂函数．
解：由幂函数的定义得:
(1)是．y=x2 (2)不是．
(3)不是． (4) 是．y=x0=1
2.利用幂函数的性质，比较下列各题中两个幂的值的大小：
解：由幂函数的单调性得:
(1)y=x1/2在[0,+∞)上递增，所以
(2)y=x-1在[0,+∞)上递减，所以
(3)y=x3在R上递增，所以
3.已知幂函数y=f(x)过(27,3),试请函数的解析式，并求f(3)．
解：设这个幂函数的解析式为y=xa，
因为过(27,3)代入得，3=27a，即a=log273=1/3.
所以这个幂函数的解析式为y=x1/3.
y=f(3)=31/3=