数学必修1 第2章 基本初等函数 本章复习(共18张PPT)
文档属性
| 名称 | 数学必修1 第2章 基本初等函数 本章复习(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 434.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
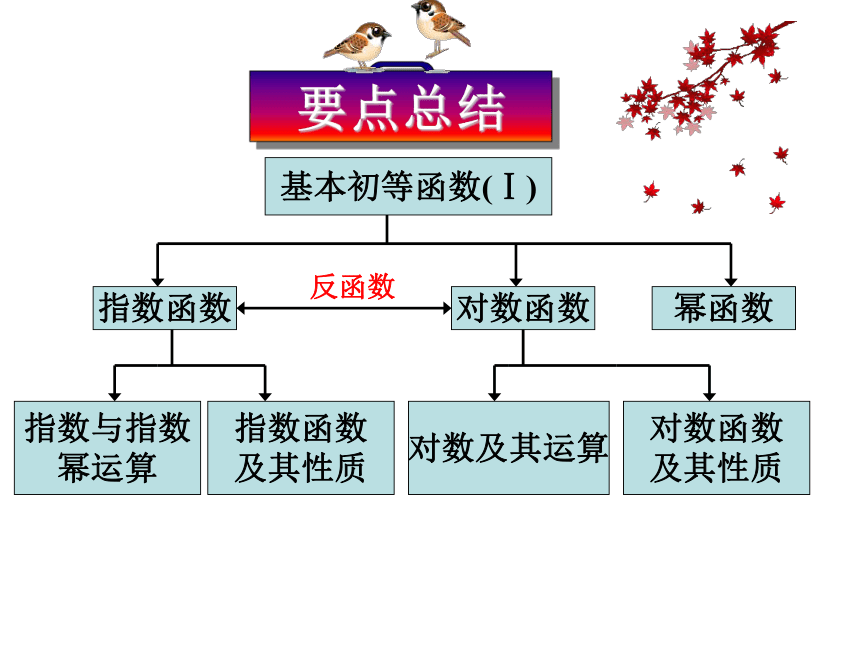
第二章 基本初等函数(I)
y=ax
y=logax
2.1 指数函数
2.2 对数函数
2.3 幂函数
y=Xa
1. 在进行指数和对数的比较过程中,有时不能直接根据性质进行直接比较,需要通过中间变量来做“搭桥”——通常情况下用“0”或“1”来做这个搭桥,以达到比较的目的.
2. 在进行指数和对数运算时,各自的运算性质和特殊值需要牢牢记得,在计算过程中灵活运用运算性质来解决计算问题.
3. 指数与对数的比较与证明,都离不开的函数图像与性质,需要熟练掌握各自函数图像与性质才能更好有效的解决以上问题,对解决综合复杂问题提供帮助.
1.根式:
2.1 指数函数
2.1.1 指数与指数幂的运算
一般地,如xn=a,那么x叫做a的n方根,其中n>1,且n∈N* .
n叫做根指数,a叫做被开方数.
2.根式意义:
当n是奇数,根式的值是唯一的;
当n是偶数且a>0,根式的值有两个,同时互为相反数;
负数没有偶次方根;
0的任何次方根都是0.
3.实指数运算性质:
2.1.2 指数函数及其性质
指数函数定义:
形如y = ax ( a?0,且a ?1)的函数叫做指数函数,其中x是自变量 .函数的定义域是R .
a>1
0 图 象
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0 性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过:
( 0 , 1 )
x>0,y>1;
x<0, 0在 R 上是
增函数
x<0,y>1;
x>0,0在 R 上是
减函数
指数函数图像与性质:
2.2 对数函数
2.2.1 对数与对数运算
对数的定义:
一般地,如果ax=N,(a>0,且a≠1)那么x叫做以a为底N的对数,记作:
x=㏒aN
其中a叫做对数的底数,N叫做真数.
对数与指数关系:
ax=N ? x=㏒aN.
(a>0,且a≠1)
对数运算性质:
2.2.2 对数函数及其性质
对数函数定义:
一般地,我们把函数
(a>0,且a≠1)叫做对数函数,其中x是自变量 ,函数的定义域是
a>1
0 图 象
性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过:
( 1, 0 )
x>1,y>0;
x<1, y<0
上增函数
x<1,y>0;
x>1, y<0
上减函数
( 0 , + ∞ )
( 0 , + ∞ )
对数函数图像与性质:
2.3 幂函数
幂函数定义:
一般地,我们把形如
叫做幂函数,其中x是自变量 , 为常数.(注:我们只研究 =1,2,3,1/2,-1时的情形)
y=x2
y=x
y=x3
y=x-1
常见5个幂函数图像:
常见5个幂函数的性质
性质
函数 定义域 值域 奇偶性 单调性 公共点
y=x R R 奇函数 R上递增 (1,1)
y=x2 R [0,+∞) 偶函数 (- ∞,0)减
(0,+ ∞)增 (1,1)
y=x-1 {x|x≠0} {y|y≠0} 奇函数 (- ∞,0),
(0,+ ∞)减 (1,1)
y=x1/2 [0,+∞) [0,+∞) 非奇非偶 [0,+∞)增 (1,1)
y=x3 R R 奇函数 R上递增 (1,1)
2. 指数函数和对数函数的图像与性质.
3. 通过给定一个函数图像,猜想和判断其函数的性质,体会数形结合的思想.
1. 指数和对数的运算性质以及变形计算.
1. 在求 时,需要主要n和a的取值.
切忌: = a.
×
2. 在比较指数式与对数式大小是,注意a的讨论.
a>1时,y=ax是增函数.
0指数函数
a>1时,y=logax是增函数.
0对数函数
a2a0.4;
loga2×
要分类讨论!
第二章 基本初等函数(I)
y=ax
y=logax
2.1 指数函数
2.2 对数函数
2.3 幂函数
y=Xa
1. 在进行指数和对数的比较过程中,有时不能直接根据性质进行直接比较,需要通过中间变量来做“搭桥”——通常情况下用“0”或“1”来做这个搭桥,以达到比较的目的.
2. 在进行指数和对数运算时,各自的运算性质和特殊值需要牢牢记得,在计算过程中灵活运用运算性质来解决计算问题.
3. 指数与对数的比较与证明,都离不开的函数图像与性质,需要熟练掌握各自函数图像与性质才能更好有效的解决以上问题,对解决综合复杂问题提供帮助.
1.根式:
2.1 指数函数
2.1.1 指数与指数幂的运算
一般地,如xn=a,那么x叫做a的n方根,其中n>1,且n∈N* .
n叫做根指数,a叫做被开方数.
2.根式意义:
当n是奇数,根式的值是唯一的;
当n是偶数且a>0,根式的值有两个,同时互为相反数;
负数没有偶次方根;
0的任何次方根都是0.
3.实指数运算性质:
2.1.2 指数函数及其性质
指数函数定义:
形如y = ax ( a?0,且a ?1)的函数叫做指数函数,其中x是自变量 .函数的定义域是R .
a>1
0
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过:
( 0 , 1 )
x>0,y>1;
x<0, 0
增函数
x<0,y>1;
x>0,0
减函数
指数函数图像与性质:
2.2 对数函数
2.2.1 对数与对数运算
对数的定义:
一般地,如果ax=N,(a>0,且a≠1)那么x叫做以a为底N的对数,记作:
x=㏒aN
其中a叫做对数的底数,N叫做真数.
对数与指数关系:
ax=N ? x=㏒aN.
(a>0,且a≠1)
对数运算性质:
2.2.2 对数函数及其性质
对数函数定义:
一般地,我们把函数
(a>0,且a≠1)叫做对数函数,其中x是自变量 ,函数的定义域是
a>1
0
性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过:
( 1, 0 )
x>1,y>0;
x<1, y<0
上增函数
x<1,y>0;
x>1, y<0
上减函数
( 0 , + ∞ )
( 0 , + ∞ )
对数函数图像与性质:
2.3 幂函数
幂函数定义:
一般地,我们把形如
叫做幂函数,其中x是自变量 , 为常数.(注:我们只研究 =1,2,3,1/2,-1时的情形)
y=x2
y=x
y=x3
y=x-1
常见5个幂函数图像:
常见5个幂函数的性质
性质
函数 定义域 值域 奇偶性 单调性 公共点
y=x R R 奇函数 R上递增 (1,1)
y=x2 R [0,+∞) 偶函数 (- ∞,0)减
(0,+ ∞)增 (1,1)
y=x-1 {x|x≠0} {y|y≠0} 奇函数 (- ∞,0),
(0,+ ∞)减 (1,1)
y=x1/2 [0,+∞) [0,+∞) 非奇非偶 [0,+∞)增 (1,1)
y=x3 R R 奇函数 R上递增 (1,1)
2. 指数函数和对数函数的图像与性质.
3. 通过给定一个函数图像,猜想和判断其函数的性质,体会数形结合的思想.
1. 指数和对数的运算性质以及变形计算.
1. 在求 时,需要主要n和a的取值.
切忌: = a.
×
2. 在比较指数式与对数式大小是,注意a的讨论.
a>1时,y=ax是增函数.
0
a>1时,y=logax是增函数.
0
a2
loga2
要分类讨论!
